Теорема Пифагора

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.), свидетельствует о гигантском числе ее конкретных реализаций.

Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.

Так, оптимист Михайло Ломоносов (1711 — 1765) писал: «Пифагор за изобретение одного геометрического правила Зевесу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».

А вот ироничный Генрих Гейне (1797 — 1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам».

И хотя сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета I (ок. 2000 до н. э.), и в вавилонских клинописных табличках эпохи царя Хаммурапи (XVIII в. до н. э.), и в древнейшем китайском трактате «Чжоу-би суань цзинь» («Математический трактат о гномоне»), время создания которого точно не известно, но где утверждается, что в XII в. до н. э. китайцы знали свойства египетского треугольника, а к VI в. до н. э. — и общий вид теоремы, и в древнеиндийском геометрическо-теологическом трактате VII — V вв. до н. э. «Сульва сутра» («Правила веревки»), — несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется. То же относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно препарировать историко-математическим скальпелем красивые древние предания.

Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Сделать это полезно еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесследно исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым. Итак,

Теорема Пифагора. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 56), чтобы убедиться в справедливости теоремы. Например, для! ABC: квадрат, построенный на гипотенузе AC, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

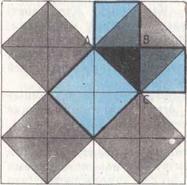
Рис 56.

Древнекитайское доказательство. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н. э. Дело в том, что в 213 г. до н. э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н. э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла «Математика в девяти книгах» — главное из сохранившихся математико-астрономических сочинений.

В IX книге «Математики» помещен чертеж (рис. 57, а), доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой c уложены так, что их внешний контур образует квадрат со стороной 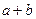, а внутренний — квадрат со стороной c, построенный на гипотенузе (рис. 57, б). Если квадрат со стороной c вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 57, в), то ясно, что образовавшаяся пустота, с одной стороны, равна 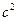, а с другой — 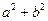т. е. 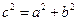. Теорема доказана.

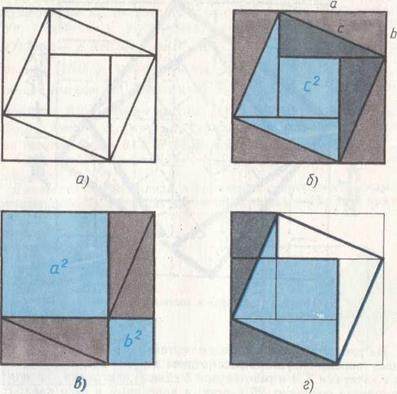
Рис. 57.

Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 57, а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно, если в квадрате со стороной c два заштрихованных треугольника (рис. 57, б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 57, г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами a и b, т. е. .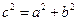

На рисунке 58 воспроизведен чертеж из трактата «Чжоу-би...». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете — 16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.

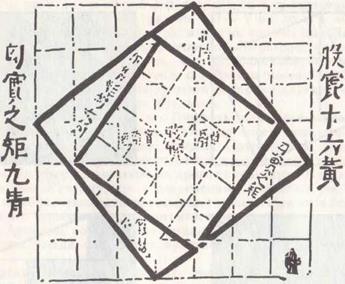
Рис. 58. «Теорема Пифагора» в древнейшем китайском трактате «Чжоу-би суань цзинь».

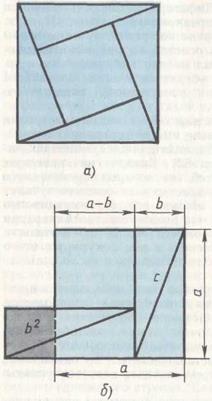
Рис. 59.

Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (рис. 59, а) с характерным для индийских доказательств словом «смотри!». Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат 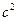перекладывается в «кресло невесты» 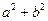(рис. 59, б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата — рис. 60) встречаются в древнеиндийском трактате «Сульва сутра» (VII — V вв. до н. э.).

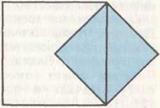
Рис. 60.

Доказательство Евклида приведено в предложении 47 I книги «Начал». На гипотенузе и катетах прямоугольного треугольника ABC строятся соответствующие квадраты (рис. 61) и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL — квадрату ACKG. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: 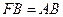, 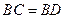и . 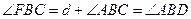Но 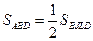, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично 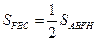(BF — общее основание, AB — общая высота). Отсюда, учитывая, что 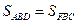, имеем 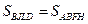. Аналогично, используя равенство треугольников BCK и ACE, доказывается, что .

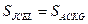Итак, 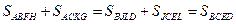, что и требовалось доказать.

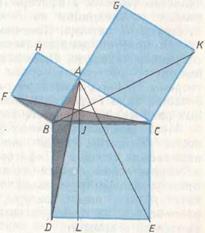
Рис. 61.

Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли «ходульным» и «надуманным». Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений I книги «Начал». Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь. Читатель может самостоятельно убедиться в этом, прочитав I книгу «Начал» и построив цепь рассуждений, аналогичную (2.3.1).

Доказательство Аннариция. Багдадский математик и астроном X в. ан-Найризий (латинизированное имя — Аннариций) в арабском комментарии к «Началам» Евклида дал следующее доказательство теоремы Пифагора (рис. 62). Квадрат на гипотенузе разбит у Аннариция на 5 частей, из которых составляются квадраты на катетах. Конечно, равенство всех соответствующих частей требует доказательства, но мы его за очевидностью оставляем читателю. Любопытно, что доказательство Аннариция является простейшим среди огромного числа доказательств теоремы Пифагора методом разбиения: в нем фигурирует всего 5 частей (или 7 треугольников). Это наименьшее число возможных разбиений. (Докажите это.)

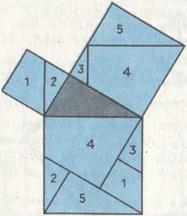
Рис. 62.

Метод равносоставленных фигур был очень популярен в древности. Вероятно, тогда же была изобретена головоломка, называемая сегодня «Пифагор». Нетрудно убедиться в том, что в основе семи частей головоломки лежат равнобедренный прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат.

Такова лишь малая толика богатств, скрытых в жемчужине античной математики — теореме Пифагора. Не случайно на обложке последнего издания «Математического энциклопедического словаря» (М.: СЭ, 1988) рисунок из древнекитайского доказательства теоремы Пифагора воспроизведен золотыми линиями в качестве символа математики.

Но почему все древние доказательства теоремы Пифагора были геометрическими? Почему древние греки так боялись алгебры и фактически свели ее к геометрии? Это очень важные вопросы, определившие весь дальнейший после Пифагора путь развития античной математики, имя которому — геометрическая алгебра.