Открытие несоизмеримости

Открытие несоизмеримости, т. е. обнаружение таких величин, отношение которых не может быть выражено с помощью отношения целых чисел, является наивысшим достижением пифагорейской школы и поворотным этапом в развитии всей математики. По силе революционизирующего воздействия это открытие, сделанное на рубеже VI — V вв. до н. э., можно сравнить разве что с открытием дифференциального и интегрального исчислений Ньютоном и Лейбницем в XVII в., открытием неевклидовой геометрии Лобачевским в XIX в. или теории относительности Эйнштейном в начале XX в.

Проблема несоизмеримости уже в античности получила громкую известность и была осознана как выдающееся достижение теоретического знания. Об этом красочно свидетельствует отрывок из диалога Платона «Законы», где некий афинянин признается в том, что долго не знал о существовании несоизмеримых величин: «Друг мой, Клиний, я и сам был поражен, что лишь так поздно узнал то состояние, в котором мы находимся. Мне показалось, что это свойственно не человеку, но скорее каким-то свиньям. Я устыдился не только за себя, но и за всех эллинов».

Мы не знаем доподлинно, решение какой конкретной задачи привело пифагорейцев к открытию несоизмеримости. Это могло быть сделано в любом из пифагорейских учений: и в арифметике при нахождении средней геометрической чисел 1 и 2, и в геометрии при отыскании общей меры диагонали и стороны квадрата, и в музыке при попытках разделить октаву пополам, что также приводит к нахождению средней геометрической между числами 1 и 2.

Как бы то ни было, но бесспорным является то, что доказательство существования несоизмеримых величин было найдено ранними пифагорейцами и к середине V в. до н. э. было широко известно. Вот это доказательство.

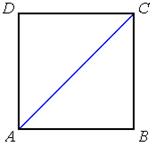
Рис. 40.

Теорема. Сторона AB и диагональ AC квадрата несоизмеримы, т. е. отношение 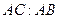не выражается отношением целых чисел (рис. 40).

Доказательство. Допустим противное. Пусть AC и AB соизмеримы, т. е. их отношение равно отношению целых чисел:

причем числа m и n одновременно не являются четными, так как иначе дробь можно было бы сократить на 2. Возводя (1.5.1) в квадрат, имеем

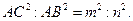
По теореме Пифагора 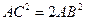, т. е. 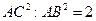, и, значит,

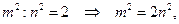
т. е. 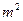четно. Согласно учению о четном и нечетном (см. с. 121) m также четно (так как произведение двух четных чисел четно, а двух нечетных—нечетно), т. е. 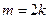, откуда 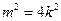. Тогда

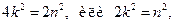
т. е. 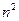четно, и, следовательно (учение о четном и нечетном), n также четно. Итак, m и n одновременно являются четными, что противоречит первоначальному допущению о несократимости дроби. Это противоречие доказывает теорему.

Как видим, доказательство несоизмеримости носит чисто пифагорейский характер, так как целиком основано на учении о четном и нечетном. Но — и в этом была трагедия пифагорейцев — родившись в недрах пифагорейского учения, это доказательство наносило смертельный удар породившему его учению. Открытие несоизмеримости опрокидывало всю философскую систему пифагорейцев, которые были убеждены, что «элементы чисел являются элементами всех вещей, и весь мир в целом является гармонией и числом». Но никаких чисел, кроме целых и их отношений, пифагорейцы не знали. И вот получалось, что для таких элементарных геометрических объектов, как диагональ и сторона квадрата, нет общей меры, т. е. нет измеряющего их числа. Какое уж там «все есть число»!

Согласно преданию, несоизмеримость открыл сам Пифагор, и это открытие долго держалось в тайне. Лишь ученик Пифагора Гиппас, как утверждает Ямвлих, «открыл недостойным участия в учениях природу пропорции и несоизмеримости». За это, продолжает Ямвлих, пифагорейцы «его столь возненавидели, что не только изгнали его из общего товарищества, но даже соорудили ему могилу, как будто некогда бывший их товарищ в самом деле ушел из земной жизни». Вскоре Гиппас действительно погиб во время кораблекрушения, и пифагорейцы видели в этом наказание богов за разглашение тайны[41].

Но, будучи истинными рыцарями науки, пифагорейцы пытались преодолеть кризис, вызванный открытием несоизмеримости. Они стали изучать эти «неразумные» величины, которые мы сегодня называем иррациональными (от лат. irrationalis — неразумный). Так, иррациональность отношения диагонали и стороны квадрата пифагорейцы объясняли тем, что оба этих отрезка состоят из бесчисленного множества точек и поэтому их отношение сводится к отношению двух бесконечно больших целых чисел. Хотя эта мысль не выдерживает критики для геометрических объектов, находящихся в рациональных отношениях (ведь они также состоят из бесчисленного множества точек!), по отношению к иррациональным числам она является справедливой. Действительно, всякое иррациональное число можно с любой степенью точности представить в виде отношения двух целых чисел, причем чем больше будут эти числа, тем точнее их отношение будет выражать иррациональное число.

В качестве иллюстрации этой пифагорейской мысли рассмотрим метод Архита — нахождение приближенных значений иррациональных чисел. Метод Архита — античного знатока пропорций — основан на музыкальной пропорции (1.4.9).

Пусть даны два числа 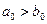. Рассмотрим их среднее арифметическое 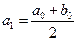и среднее гармоническое 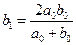. Как мы показали (см. с. 140), 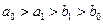и 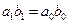. Затем образуем те же средние из полученных значени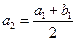и: и 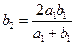и т. д. В результате получим две последовательности:

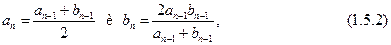
обладающие следующим свойством:

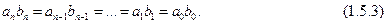
Обозначая 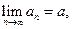, 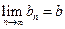и переходя в равенствах (1.5.2) к пределу при 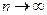, имеем

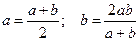
откуда легко находим, что 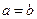. Учитывая это равенство и переходя к пределу в (1.5.3), получим

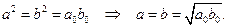
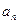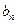Итак, обе последовательности и при 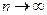стремятся к числу .

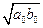Пусть теперь 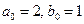. Эти числа можно рассматривать как нулевые приближения числа 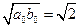, которое будет пределом последовательносте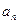й и 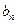. Найдем первые члены этих последовательностей:

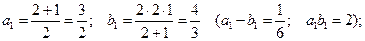
вторые члены:

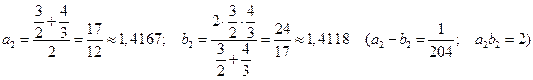
и третьи члены:

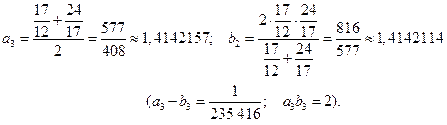
Как видим, последовательност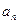и и 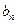очень быстро сходятся к своему пределу и уже их третьи члены дают прекрасное приближение (пять верных знаков!) числа 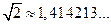( 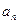— с избытком и 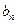— с недостатком). Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что, чем больше целые числа в отношении, тем точнее они выражают иррациональное число.

Достаточно быстро было обнаружено, что диагональ и сторона квадрата не составляют исключения. К концу V в. до н. э. пифагореец Феодор из Кирены (? — 369 до н. э.), математик, астроном и музыковед, учитель Платона, показал, что стороны квадратов, площади которых равны 3, 5, 6,..., 15, несоизмеримы со стороной единичного квадрата, т. е. числа 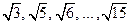иррациональные.

Мы не знаем доказательства Феодора, но ясно, что он рассматривал каждую иррациональность в отдельности. Существуют различные гипотезы относительно того, почему Феодор не смог доказать иррациональность следующего числа: 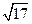и выше. Наиболее убедительная из них утверждает, что все доказательства Феодора основывались только на учении о четном и нечетном, а первое число, для которого этот способ не проходит, как раз и есть .

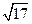Но уже в самом начале IV в. до н. э. (по-видимому, в 399 г. до н. э., в год казни Сократа) юным и талантливым учеником Феодора Теэтетом было получено общее доказательство иррациональности чисел вида 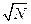, где N — целое число, не являющееся полным квадратом. В своем доказательстве Теэтет, по-видимому, опирался на основную теорему созданной им же теории делимости: произведение двух целых чисел AB делится на простое число P тогда и только тогда, когда по крайней мере один из сомножителей делится на P. Если знать эту теорему, то доказательство иррациональности 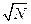(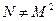) фактически не отличается от доказательства иррациональности 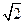. Позднее Теэтет доказал иррациональность чисел вида 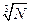, (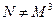) а также рассмотрел иррациональности вида 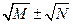, , 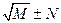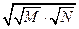и предпринял попытку классификации иррациональностей. Эти результаты Теэтета собраны в X, наиболее трудной, книге «Начал» Евклида.

Итак, открытие несоизмеримости не загнало пифагорейцев в тупик, но, напротив, стимулировало развитие новых, красивых и глубоких теорий. Открытие несоизмеримости было едва ли не первым теоретическим результатом, который невозможно получить с помощью опыта. Более того, оно противоречило всей измерительной практике, ибо в жизни все величины соизмеримы в пределах точности измерительного инструмента. Таким образом, открытие несоизмеримости было сделано не благодаря опыту, а вопреки ему, и в этом его можно сравнить с открытием Коперника, который «остановил Солнце» вопреки нашим ежедневным наблюдениям.

Открытие несоизмеримости оказало решающее влияние на все дальнейшее развитие греческой математики. Поскольку некоторые геометрические объекты не измерялись отношением целых чисел, то естественно было предположить, что геометрические объекты являются величинами более общей природы, чем рациональные числа. Поэтому уже в пифагорейской школе предпринимается попытка построить всю математику, основываясь не на арифметике, а на геометрии. Для этого величины (и в первую очередь числа) представлялись отрезками, площадями и все алгебраические операции (в том числе и извлечение корня) интерпретировались геометрически. Более того, геометрически записывались и решались даже уравнения.

Так в пифагорейской школе родилась «геометрическая алгебра», а на первое место в пифагорейской μάθημα вышла геометрия.