Пентаграмма

Почему именно пентаграмму пифагорейцы выбрали в качестве символа приветствия и тайного опознавательного знака? Возможно, знакомство с математическими свойствами пентаграммы поможет нам ответить на этот вопрос.

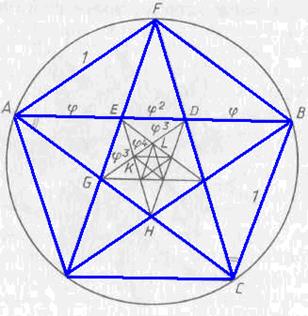
Рис. 50.

Пусть окружность разделена на пять равных частей. Соединяя последовательно точки деления, получим правильный пятиугольник, диагонали которого образуют пятиконечную звезду, или звездчатый пятиугольник. Это и есть пентаграмма (πεντά — γραμμον, πέντε — пять + γράμμα — черта, линия). Легко видеть, что внутри пятиконечной звезды вновь образуется правильный пятиугольник, диагонали которого дают новую звезду, и т. д. (рис. 50).

Рассмотрим треугольник ABC. Он равнобедренный, так как хорды AB и AC стягивают равные дуги. Далее, 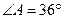, 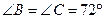как вписанные в окружность углы, опирающиеся на дуги в 72° (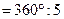) и в 144° (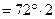) соответственно. Но 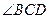равен 36° как опирающийся на дугу FB в 72°, и, следовательно, CD является биссектрисой в 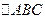и отсекает от него 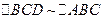. Из подобия этих треугольников имеем 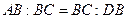. Учитывая, что 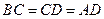(так как в 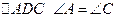и, следовательно, 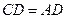), приходим к пропорции

т. е. данный отрезок AB так относится к его большей части AD, как большая часть относится к меньшей BD. Иначе говоря, точка D делит отрезок AB в золотой пропорции (см. (1.4.7)).

Итак, равнобедренный треугольник, у которого углы при основании (72°) вдвое больше угла при вершине (36°), обладает уникальным свойством: биссектриса угла при основании делит противоположную сторону в золотом сечении. За свое замечательное свойство этот треугольник был прозван средневековыми математиками возвышенным.

Именно золотое свойство возвышенного треугольника и использовал Евклид для его построения, а значит, и для построения правильного пятиугольника (см. с. 148). В самом деле, если данный отрезок AB точкой D разделить в золотой пропорции, а затем циркулем из точки B сделать засечку радиусом AD, а из точки A — радиусом AB, то точка пересечения C и будет вершиной возвышенного треугольника ABC. Далее остается лишь описать окружность около ABC и провести биссектрисы углов B и C до пересечения с окружностью. Окружность разделена на пять равных частей, и, значит, правильный пятиугольник готов.

Остается показать, как во времена Евклида делили отрезок в золотой пропорции. Мы знаем (с. 138), что величина x, делящая отрезок a в золотом сечении, удовлетворяет уравнению

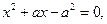
положительный корень которого можно представить в виде

Греки это решение находили геометрически. В самом деле, подкоренное выражение в (2.2.2), согласно теореме Пифагора, можно рассматривать как гипотенузу треугольника с катетами a и 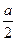(или как диагональ двойного квадрата со стороной 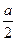). Отнимая с помощью циркуля от гипотенузы отрезок 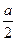, мы и найдем искомую величину x. Остается только (опять-таки с помощью циркуля) перенести отрезок x на отрезок a (рис. 51). Золотое сечение отрезка a построено. Заметим, что способ построения золотого сечения с помощью двойного квадрата был известен и древним египтянам.

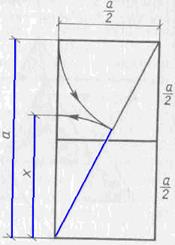
Рис. 51.

Но вернемся к пентаграмме. Принимая сторону исходного правильного пятиугольника за единицу 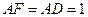, полагая 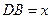и, следовательно, 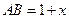и подставляя все это в (2.2.1), приходим к уравнению

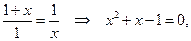
которое имеет единственный положительный корень:

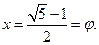
Так как

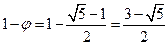
и

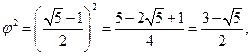
то

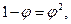
и мы окончательно находим

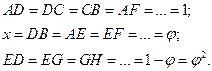
Повторяя наши рассуждения для 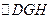, в котором 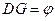, легко видеть, что стороны внутренней звезды будут равны 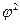, а стороны ее внутреннего правильного пятиугольника — 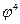и т. д. (см. рис. 50).

Таким образом, последовательность правильных пятиугольников и вписанных в них звезд образует бесконечно убывающую геометрическую прогрессию со знаменателем 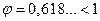, или ряд золотого сечения:

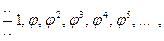
причем стороны правильных пятиугольников образуют ряд четных степеней:

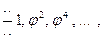
а стороны звезд — ряд нечетных степеней:

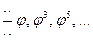
Наконец, если продолжить стороны правильного пятиугольника до пересечения, то получим звезду, сторона у которой находится со стороной исходного пятиугольника 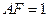в золотой пропорции, т. е.

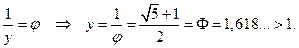
Итак, данную пентаграмму можно неограниченно продолжать как в сторону уменьшения, так и в сторону увеличения. При этом стороны правильных пятиугольников и вписанных в них звезд образуют ряд золотого сечения общего вида

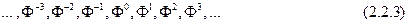
или

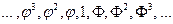
Из множества геометрических прогрессий ряд (2.2.3) отличается замечательным свойством, называемым аддитивным свойством: сумма двух соседних членов ряда равна следующему члену ряда:

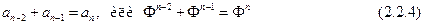
В самом деле, поскольку 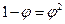, то

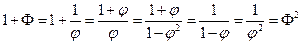
и, значит,

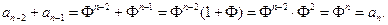
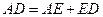
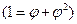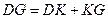
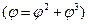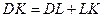
Аддитивное свойство ряда золотого сечения прекрасно видно на пентаграмме (рис. 50): , , 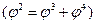и т. д.

Именно благодаря аддитивному свойству ряд золотого сечения играет важнейшую роль в архитектуре, в том числе и в архитектуре Древней Греции. Архитектурное произведение (как, впрочем, и любое произведение искусства) смотрится как единое целое, гармонично, когда все его части находятся в непрерывной пропорциональной зависимости (это знаменитый принцип гармонии, сформулированный еще Гераклитом: «Из всего — единое и из единого — все»):

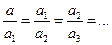
Но вместе с тем эти части должны образовывать целое, т. е.

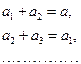
Одновременно выполнение этих двух условий может обеспечить только ряд золотого сечения.

Итак, пентаграмма обладает массой интереснейших математических свойств:

1. Лучи пентаграммы делят друг друга в золотой пропорции:

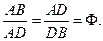
2. Сторона правильного пятиугольника, сторона вписанной в него пентаграммы и сторона образованного пентаграммой внутреннего пятиугольника также относятся в золотой пропорции:

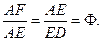
3. Лучи пентаграммы, выходящие из одной точки, образуют возвышенный треугольник.

4. Последовательность сторон правильных пятиугольников и вписанных в них пентаграмм образует ряд золотого сечения:

который является бесконечно убывающей геометрической прогрессией со знаменателем и обладает аддитивным свойством:

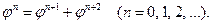
5. Отрезки пентаграммы 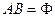, , 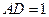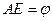и 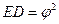связаны между собой всеми видами средних (1.4.6), известных пифагорейцам, а именно

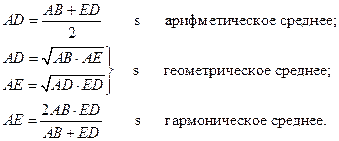
В общем случае для четырех последовательных членов ряда (2.2.5) 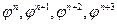нетрудно доказать соотношения

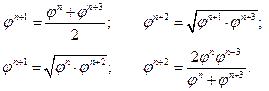
Подведем итог. Мы видим, что пентаграмма буквально соткана из золотой пропорции и всех видов средних. Можно только догадываться, в какой священный восторг приводило пифагорейцев столь редкое обилие математических свойств в одной геометрической фигуре! К математике присоединялась и числовая мистика: число 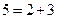было для пифагорейцев числом любви как сумма первого женского (2) и первого мужского (3) чисел. Теперь становится понятным, почему именно пентаграмма была выбрана пифагорейцами в качестве символа жизни и здоровья.

Столь необычайно пропорциональное строение пентаграммы, красота ее внутреннего математического содержания являются основой и красоты ее внешней формы. Пентаграмма пропорциональна и, значит, красива. Не случайно и сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира.

Но первыми, кто обратил пятиконечную звезду в символ, были опять-таки пифагорейцы.