Правильные фигуры и тела

«Пифагор преобразовал геометрию, придав ей форму свободной науки, рассматривая ее принципы чисто абстрактным образом и исследуя теоремы с нематериальной, интеллектуальной точки зрения. Именно он нашел теорию иррациональных количеств и конструкцию космических тел». Так оценивал вклад Пифагора в геометрию Прокл, и эта оценка античного философа совершенно справедлива.

В самом деле, в школе Пифагора геометрия оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически — как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию. При этом, что самое главное, свойства геометрических фигур устанавливались пифагорейцами не путем измерений, а с помощью логических доказательств.

Обладая широчайшей областью практических приложений, геометрия первой из учений пифагорейской μάθημα сбросила пелену «секретности» и стала самой популярной наукой. Впрочем, Ямвлих в «Жизни Пифагора» причины популярности геометрии представлял несколько иначе: «Вот как пифагорейцы объясняют, почему геометрия стала открыто распространяться. Это произошло по вине одного из них, который потерял деньги пифагорейской общины. После этого несчастья община позволила ему зарабатывать деньги при помощи геометрии — и геометрия получила название «Предание Пифагора». Памятуя, что в V в. до н. э. были весьма популярны софисты — странствующие учителя мудрости, вполне возможно, что и пифагорейцы не гнушались пополнять казну преподаванием.

Но каково было содержание «Предания Пифагора» — первого греческого учебника геометрии? К сожалению, мы этого не знаем. Однако сохранились фрагменты из сочинений замечательного греческого математика середины V в. до н. э. Гиппократа с ионийского острова Хиоса[42]. Так вот, в сочинениях Гиппократа Хиосского свойства плоских прямолинейных фигур предполагаются хорошо известными, тогда как свойства круга и хорд подробно изучаются. Поскольку до Гиппократа геометрией занимались только пифагорейцы, то естественно предположить, что все, что Гиппократ считает хорошо известным, было открыто пифагорейцами.

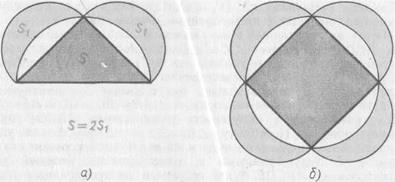
Рис. 41.

Таким образом, благодаря Гиппократу Хиосскому у нас есть основания считать, что пифагорейцы в целом построили всю планиметрию прямолинейных фигур. Они изучили свойства треугольников, прямоугольников, параллелограммов, трапеций, доказали теорему о сумме углов треугольников, теорему о стороне треугольника, лежащей против тупого угла, теоремы о равновеликости треугольников. Вершиной же планиметрии прямолинейных фигур явилось доказательство знаменитой теоремы Пифагора. Эти результаты пифагорейской геометрии, по-видимому, и составили основу I книги «Начал» Евклида, которая завершается теоремой Пифагора.

Пифагорейцы проявляли повышенный интерес к правильным фигурам и телам. Правильные геометрические формы благодаря их «правильности», т. е. наличию зеркальной или поворотной (а часто и той и другой) симметрии, как нельзя более отвечали всей пифагорейской философии о закономерном, структурно-упорядоченном гармоничном устройстве мироздания. (К этому вопросу мы еще вернемся в пп. 2.2 и 4.3.) Геометрические формы, в особенности правильные, наиболее выразительно выявляли число и как нельзя более подходили для «извлечения числа из вещей». Пифагорейцы раскладывали одни геометрические формы на другие (чаще на правильные или «несущие» какие-либо «священные» числа) и в этом видели постижение внутренней взаимосвязи явлений.

Вот почему пифагорейцы придавали особое значение доказанной ими теореме о том, что плоскость можно сплошь (т. е. без «дырок» и наложений) покрыть лишь тремя правильными многоугольниками: треугольниками, квадратами и шестиугольниками (рис. 42). Доказательство этой теоремы достаточно прозрачно, и мы его оставляем читателю. Не представляет труда и построение этих правильных фигур, а также фигур, получаемых из них удвоением сторон.

Рис. 42.

Но вот построение правильного пятиугольника уже не столь очевидно. Мы не знаем, как строили правильный пятиугольник пифагорейцы. Но известно, что пятиконечную звезду — свой главный символ и опознавательный знак — они складывали из трех равнобедренных треугольников. А это явно перекликается с методом построения правильного пятиугольника, описанным у Евклида («Начала», кн. IV, пред. 11). Так что метод Евклида, возможно, восходит к пифагорейцам. Рассмотрим его.

Пусть дан вписанный в окружность равнобедренный треугольник ACD, у которого 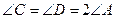. (Способ построения такого треугольника мы укажем в п. 2.2.) Проведем биссектрисы CE и DB углов C и D соответственно. Тогда углы 1 — 5 (рис. 43) будут равны, а следовательно, будут равны соответствующие им дуги и стягивающие их хорды, т. е. 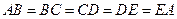. Итак, вписанный в окружность пятиугольник ABCDE будет равносторонним. Поскольку 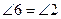и 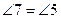как углы, опирающиеся на одинаковые дуги AE и AB соответственно, то все углы 1 — 7 будут равными и, следовательно, каждый угол пятиугольника ABCDE будет составлен из трех равных углов, т. е. 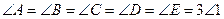. Таким образом, построенный пятиугольник является равносторонним и равноугольным, т. е. правильным.

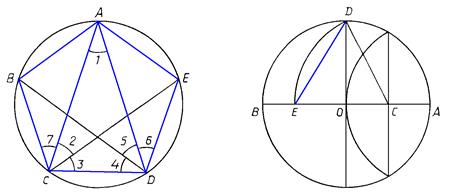
Рис. 43. Рис. 44.

Со временем древнегреческими математиками был найден более простой способ построения правильного пятиугольника. Он описан в другом выдающемся сочинении античности — «Альмагесте» Птолемея (ок. 150), которое, подобно «Началам» Евклида в геометрии, является энциклопедией античных знаний по астрономии. Птолемей делит радиус окружности OA пополам (точка C) и радиусом CD описывает окружность до пересечения с диаметром AB в точке E (рис. 44). Тогда ED и есть сторона правильного пятиугольника. (После прочтения п. 2.2 читатель без труда докажет это самостоятельно.)

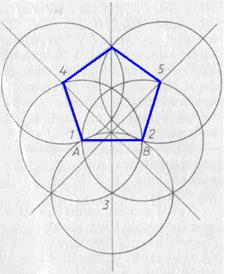
Рис. 45.

Еще через полтора тысячелетия, в 1525 г., Альбрехт Дюрер (1471 — 1528), художник и ученый, один из титанов эпохи Возрождения, в трактате «Руководство к измерению при помощи циркуля и линейки» указал приближенный способ построения правильного пятиугольника по заданной стороне AB с помощью «заржавевшего» циркуля, т. е. одним раствором циркуля. Способ Дюрера понятен из рисунка 45, где цифрами последовательно обозначены положения ножки циркуля. Метод Дюрера отличается большой точностью (углы 1 и 2 равны не 108°, а 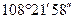, углы 4 и 5 чуть больше 107°, а угол C чуть больше 109°), так что его погрешности на глаз совершенно не воспринимаются. Сам Дюрер ни словом не обмолвился о приближенном характере своих построений, возможно, считая их точными. И тем не менее метод Дюрера является приближенным. (Попробуйте доказать это.)

А как построить с помощью циркуля и линейки следующую правильную фигуру — семиугольник? Эта задача оказалась непосильной не только древним пифагорейцам, но оставалась неразрешенной более двух тысячелетий! Лишь в 1796 г. 19-летний немецкий юноша Карл Фридрих Гаусс (1777 — 1855), прозванный позднее королем математиков, решил ее. Гаусс показал, что задача построения с помощью циркуля и линейки правильного n -угольника, равносильная задаче деления окружности на n равных частей, связана с изучением корней уравнения 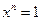. Далее Гаусс доказал, что правильный N -угольник может быть построен циркулем и линейкой в том и только том случае, когда N — простое число вида

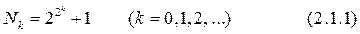
Простые числа вида (2.1.1) называются числами Ферма, и до сих пор известно лишь пять таких чисел: .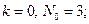

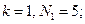
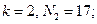
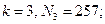
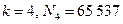Этот результат Гаусса обобщается на случай, когда число сторон многоугольника n является произведением чисел вида (2.1.1). Учитывая также возможность удвоения n, сформулируем теорему Гаусса: правильный многоугольник можно построить с помощью циркуля и линейки тогда и только тогда, когда число его сторон имеет вид

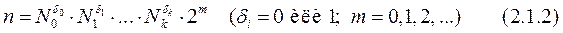
Фактически в 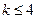, так как других чисел Ферма пока неизвестно.

Легко видеть, что все многоугольники, которые умели строить древние греки, а именно те, у которых 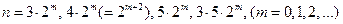, содержатся в (2.1.2). Таким образом, к античным многоугольникам добавились новые с n = 17, 34, 51, 68, 85, 126, 252, 255, 257,..., причем принципиально новыми из них являются 17-угольник, 257-угольник и 65 537-угольник. Гаусс нашел метод построения первых двух многоугольников. Заметим, что описание метода построения правильного 257-угольника заняло у Гаусса около полусотни страниц. Гаусс всю жизнь чрезвычайно гордился своим юношеским открытием и завещал выгравировать на своем надгробии правильный 17-угольник, вписанный в круг.

Итак, правильный многоугольник построить циркулем и линейкой можно при n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, …, нельзя при n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33,...

Так в самом конце XVIII в. была решена проблема, поставленная более 2000 лет назад пифагорейцами. Ее решение помимо гения самого Гаусса потребовало и всей суммы математических знаний, накопленных человечеством за два тысячелетия. Нам же остается лишь вновь в восхищении спросить себя: откуда у пифагорейцев была столь безупречная интуиция на «вечные» математические проблемы?

Перейдем теперь к правильным многогранникам. Их всего пять, и Прокл помимо замечательных открытий в планиметрии приписывает Пифагору построение всех пяти правильных тел. Однако сегодня историки математики предпочитают верить не Проклу, а обнаруженной схолии (σχόλιον — толкование, объяснение) в XIII книге «Начал» Евклида, где говорится, что Пифагор знал лишь три правильных тела — тетраэдр, гексаэдр (куб) и додекаэдр, а позднее Теэтет открыл и два оставшихся — октаэдр и икосаэдр. И в том и в другом случае эти античные свидетельства говорят нам об интересе пифагорейцев к правильным телам.

По-видимому, сама природа подсказала пифагорейцам форму правильных тел: кристаллы поваренной соли имеют форму куба, кристаллы квасцов — октаэдра, а кристаллы пирита — додекаэдра. Последний, как показывают раскопки в Италии, был любимой игрушкой этрусских детей во времена Пифагора.

Название правильному многограннику дается по числу его граней (например, тетраэдр — τετρά-εδρον — τετράς — четыpe + εσρα — область, часть тела, грань — четырехгранник). Правильные многогранники показаны на рисунке 46, а их геометрические характеристики собраны в таблице, где m обозначает число граней при вершине.

Правильный многогранник	Число	Геометрия грани	m
граней, M	вершин, L	ребер, N
Тетраэдр	4 (тетра)			∆
Октаэдр	8 (окто)			∆
Икосаэдр	20 (икоси)			∆
Гексаэдр	6 (гекса)			□
Додекаэдр	12 (додека)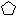

Пифагорейцы заметили, что в кубе число вершин (8) есть среднее гармоническое числа граней (6) и числа ребер (12) и поэтому называли куб гармоническим телом. Особое предназначение куба виделось также и в том, что он единственный из правильных тел сплошь заполняет пространство.

Ко времени Евклида было замечено, что куб и октаэдр, а также додекаэдр и икосаэдр дуальны (двойственны), т. е. число граней одного тела равно числу вершин другого и наоборот. Тогда одно тело может быть получено из другого, если центры тяжести граней одного принять за вершины другого или наоборот (рис. 46). Тетраэдр дуален сам себе.

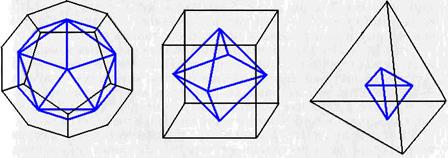
Рис. 46

Однако важнейшее свойство выпуклых многогранников было установлено лишь в середине XVIII в. теоремой Эйлера: во всяком выпуклом многограннике число вершин (L) плюс число граней (M) минус число ребер (N) есть величина постоянная, равная двум:

К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел — они выходят далеко за рамки нашей книги. Заметим только, что строгое построение всех правильных тел было дано в XIII книге «Начал» Евклида, которая является венцом всего великого сочинения[43]. Как построение правильного многоугольника начинается с окружности, точно так же и сфера является основой для построения правильного многогранника. Как в правильном многоугольнике центры вписанной и описанной окружностей совпадают, так и в правильном многограннике совпадают центры вписанной и описанной сфер. Последнее свойство легло в основу кеплеровской модели Вселенной, которую мы рассмотрим в п. 4.3.

И все-таки самым интригующим свойством правильных тел является то, что их существует всего пять. Не случайно доказательством этого факта завершалась последняя XIII книга «Начал» Евклида[44]. В самом деле, сумма плоских углов S при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине 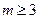. Значит, гранями правильных тел могут быть только три правильных многоугольника: треугольник, квадрат и пятиугольник, ибо уже для шестиугольника 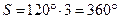. Из правильных треугольников можно составить три правильных тела: 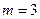— тетраэдр, 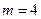— октаэдр и 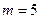— икосаэдр (при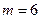 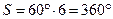). Из квадратов и правильных пятиугольников — только по одному (куб и додекаэдр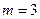) при (при 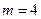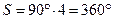— для квадратов и 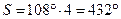— для пятиугольников). Таким образом, правильных многогранников может быть только пять.

Этот факт не мог оставить равнодушными склонных к числовой мистике пифагорейцев, а вслед за ними Платона и неоплатоников. Платон развил знаменитое учение о пяти «стихиях» — основах мироздания, атомы которых он мыслил в виде правильных тел. (Подробнее это учение Платона мы рассмотрим в п. 4.3.) С тех пор правильные многогранники часто называют телами Платона.

Правильные многогранники на протяжении всей истории человечества не переставали восхищать пытливые умы симметрией, мудростью и совершенством своих форм. Леонардо да Винчи любил мастерить каркасы правильных тел и преподносить их в дар знатным особам, возможно, пытаясь таким образом приобщить сильных мира сего к философским размышлениям о красоте вечных истин (рис. 47).

Рис. 47. Рисунки деревянных моделей додекаэдра и икосаэдра, выполненные Леонардо да Винчи для книги его друга Луки Пачоли «О божественной пропорции». Венеция. 1509 г.

Но на пяти правильных телах история многогранников не остановилась. Вслед за правильными телами Платона были открыты полуправильные тела Архимеда, грани которых составлены из правильных равных многоугольников нескольких видов, причем в каждой вершине сходится одно и то же число одинаковых граней в одинаковом порядке и многогранные углы при вершинах равны. Заметим, что тела Архимеда могут быть получены из соответствующих тел Платона снятием равных фасок. Тел Архимеда всего 13. Любопытно, что во второй половине XX в. было обнаружено еще одно тело Архимеда — псевдоромбокубооктаэдр, которое не может быть получено путем однотипных усечений тела Платона и поэтому в течение 2000 лет оставалось незамеченным.

В XVII в. Кеплером и в XVIII в. Пуансо были найдены различные формы звездчатых невыпуклых многогранников, получаемых продолжением граней правильного или полуправильного тела до самопересечения. Простейшее тело такого типа — «звезда Кеплера» — было обнаружено Кеплером в 1619 г. и получается продолжением граней октаэдра (рис. 48). Впрочем, это же тело можно представить и как пересечение двух тетраэдров. Звездчатые многогранники поражают воображение красотой и причудливым разнообразием своих форм (рис. 49). Тем, кого вдохновит эта форма, мы рекомендуем книгу М. Венниджера «Модели многогранников» (М.: Мир, 1974), познакомившись с которой можно на свой вкус выбрать и сделать самый экзотический звездчатый многогранник.

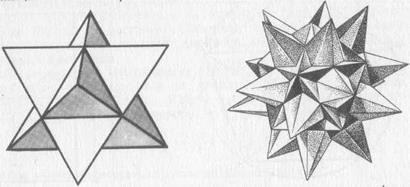
Рис. 48. Рис. 49. Седьмая звездчатая форма тела Архимеда — икосододекаэдр.

И все-таки знакомство с многогранниками мы советуем начать с «Начал» Евклида, ибо, как сказал Альберт Эйнштейн, «Тот не рожден для теоретических исследований, кто в молодости не восхищался этим творением».