Основные понятия математической логики

ДМ 1. ОСНОВННЫЕ ПОНЯТИЯ

ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Основные понятия математической логики

Высказыванием называется предложение, о котором можно судить, истинно оно или ложно.

Действия над высказываниями заключаются в том, что при помощи связок из одних высказываний образуются новые высказывания. Результат действия называется также как и само действие.


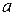
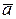
И	Л
Л	И

Отрицание (иначе инверсия) сводится в присоединении к высказыванию a связки «не». В результате получается высказывание «не a», также как и действие называемое отрицанием высказывания a. Результат обозначается 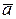. Отрицание истинно, если исходное высказывание ложно; отрицание ложно, если исходное высказывание истинно.

Определение истинностного значения отрицания можно записать в виде таблицы.

a	b	a Ù b
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Конъюнкция высказываний a, b образуется с помощью связки «и», обозначаемой символом Ù. Конъюнкция a Ù b истинна тогда и только тогда, когда истинны оба образующих её высказывания (см. таблицу).

a	b	a Ú b
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

Дизъюнкция высказываний a, b образуется с помощью связки «или», обозначаемой символом Ú. Дизъюнкция a Ú b истинна тогда и только тогда, когда истинно хотя бы одно из образующих её высказываний (см. таблицу).

a	b	a Å b
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Эксорция (исключающее или) высказываний a, b образуется с помощью связки «[либо] …, либо …»[1], обозначаемой символом Å. Дизъюнкция a Å b истинна тогда и только тогда, когда одно из образующих её высказываний истинно, а другое ложно (см. таблицу).

Импликация высказываний a, b образуется с помощью связки «если

a	b	a Þ b
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

…, то …», обозначаемой символом Þ (a Þ b, читается «если a, то b» или «из a, следует b», или «a влечёт b»). В этом выражении высказывание a называется посылкой, а высказывание b — следствием или заключением. Импликация ложна тогда и только тогда, когда посылка истинна, а заключение ложно (см. таблицу).

a	b	a Û b
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Эквиваленция (или равносильность) высказываний a, b образуется с помощью связки «… равносильно …» или «тогда и только тогда, когда …», обозначаемой символом Û (a Û b, читается «a равносильно b»). Эквиваленция истинна тогда, если значения истинности образующих высказываний совпадают (см. таблицу).