Множество X, на котором заданы алгебраические действия (операции), называется алгебраической структурой (или алгебраической системой). Множество X называется носителем алгебры, а список операторов (знаков действий) — сигнатурой алгебры. Для алгебры важно, чтобы действия проводились над любыми элементами множества, и результатом являлся элемент этого же множества.
На множестве N всюду определены сложение и умножение. Потребность включения в алгебру вычитания привела к понятиям отрицательных чисел и нуля. Множество целых чисел Z получает дальнейшее обобщение в связи с тем, что на нём не всюду определено деление, появляются дроби. Множество рациональных чисел Q можно считать замкнутым относительно операций +, –, ×, /, с единственной оговоркой — неопределенно деление на нуль. Рассмотрение других действий приводит к открытию иррациональных чисел, которые в совокупности с рациональными образуют множество действительных чисел R. В дальнейшем потребность всюду определить операции возведения в дробную степень привела к открытию комплексных чисел.
Множество высказываний также является алгебраической системой.
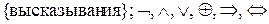 .
.
Алгебраической системой является также булеан любого множества. На нем определены операции пересечения, объединения, вычитания и дополнения:
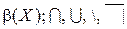 .
.
Латинский алфавит
| Буква | Название | Буква | Название |
| Aa | А | Nn | Эн |
| Bb | Бэ | Oo | О |
| Cc | Цэ | Pp | Пэ |
| Dd | Дэ | Ку | |
| Ee | Е | Rr | Эр |
| Ff | Эф | Ss | Эс |
| Gg | Гэ (Же)[6] | Tt | Тэ |
| Hh | Ха (Аш) | Uu | У |
| Ii | И | Vv | Вэ |
| Jj | Йот (Жи) | Ww | Дубль вэ |
| Kk | Ка | Xx | Икс |
| Ll | Эль | Yy | Игрек |
| Mm | Эм | Zz | Зэт |
[1] В квадратные скобки обычно заключают элемент выражения, который можно опустить.
[2] Использовано общепринятое сокращенное обозначение дней недели.
[3] Gen — сокр. слова генерация (порождение).
[4] Такие наглядные изображения называют диаграммами Венна (в честь английского математика и логика Джона Венна), хотя известно, что ими пользовался Л. Эйлер задолго до появления теории множеств.
[5] В честь английского математика и логика Джорджа Буля.
[6] В скобках указаны французские названия букв, параллельно употребляемые в русскоязычной математической традиции.
 2015-09-06
2015-09-06 432
432







