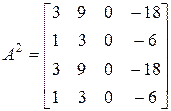 ,
,
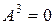 , то
, то  — нильпотентный оператор индекса 3. Строим подпространства
— нильпотентный оператор индекса 3. Строим подпространства 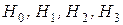 .
.
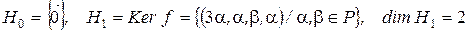 ,
,
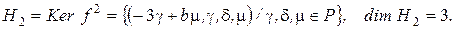
Находим систему векторов, дополняющую базис 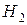 до базиса
до базиса 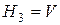 . Она будет состоять из одного вектора, так как
. Она будет состоять из одного вектора, так как 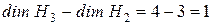 . Вектор
. Вектор 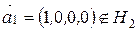 и, значит, будет искомым. Находим
и, значит, будет искомым. Находим 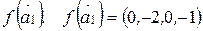 . Так как
. Так как 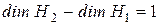 , то вектор
, то вектор 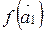 дополняет базис
дополняет базис 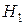 до базиса
до базиса 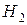 . Находим
. Находим 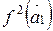 .
. 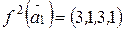 . Так как
. Так как 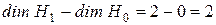 , то ищем вектор
, то ищем вектор 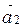 такой, что система
такой, что система 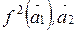 дополняет базис
дополняет базис 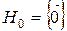 до базиса
до базиса 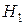 , т.е. такой, что система
, т.е. такой, что система 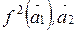 является базисом
является базисом 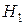 . Очевидно, вектор
. Очевидно, вектор 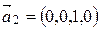 является искомым. Следовательно, система
является искомым. Следовательно, система 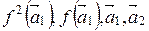 - искомый канонический базис. Матрица
- искомый канонический базис. Матрица 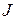 оператора
оператора  в этом базисе равна
в этом базисе равна
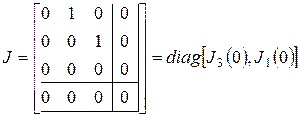 .
.
Иногда достаточно знать матрицу нильпотентного оператора в каноническом базисе, не находя самого базиса. Ответ на такой вопрос дает
Теорема 2. Пусть 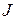 — жорданова нормальная форма матрицы нильпотентного оператора
— жорданова нормальная форма матрицы нильпотентного оператора 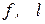 — число всех клеток Жордана, стоящих “на диагонали” матрицы
— число всех клеток Жордана, стоящих “на диагонали” матрицы 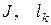 — число всех клеток Жордана порядка
— число всех клеток Жордана порядка 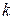 , стоящих “на диагонали” матрицы
, стоящих “на диагонали” матрицы 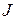 .
.
Тогда
1. 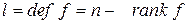 .
.
2. 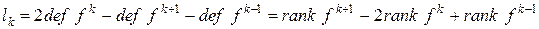
3. Максимальный размер клеток Жордана матрицы 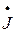 равен индексу нильпотентности оператора
равен индексу нильпотентности оператора  .
.
Доказательство. Заметим, что в жордановой нормальной форме матрицы линейного оператора на диагонали стоят собственные значения этого оператора вместе с их кратностями и только они. Так как в каноническом базисе (3), построенном в доказательстве теоремы I, матрица оператора  жорданова и состоит из клеток Жордана с нулем на диагонали, то все собственные значения оператора
жорданова и состоит из клеток Жордана с нулем на диагонали, то все собственные значения оператора  равны нулю. Поэтому матрица
равны нулю. Поэтому матрица 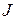 содержит лишь клетки Жордана с элементом 0 на диагонали, т.е.
содержит лишь клетки Жордана с элементом 0 на диагонали, т.е.
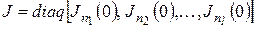 .
.
Очевидно, ранг матрицы 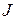 равен
равен 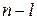 . Так как ранг линейного оператора совпадает с рангом его матрицы, то
. Так как ранг линейного оператора совпадает с рангом его матрицы, то 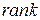
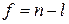 . Отсюда
. Отсюда
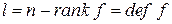 . Заметим, что дефект нильпотентного оператора равен максимальному числу линейно независимых собственных векторов этого оператора.
. Заметим, что дефект нильпотентного оператора равен максимальному числу линейно независимых собственных векторов этого оператора.
Далее, непосредственные вычисления показывают, что
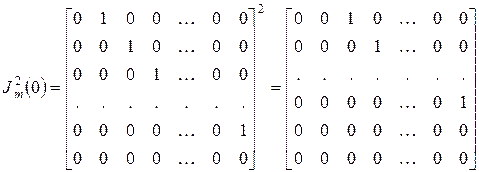 ,
,
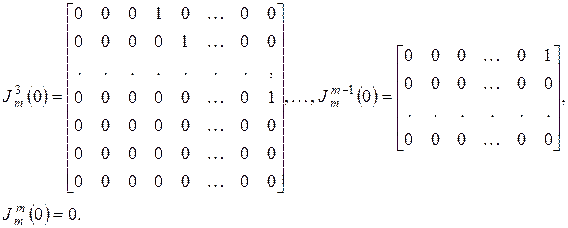 ,
,
Если теперь 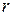 - максимальный порядок клеток Жордана матрицы
- максимальный порядок клеток Жордана матрицы 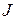 , то
, то 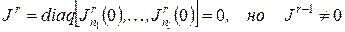 . В силу равносильности равенств
. В силу равносильности равенств 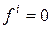 и
и 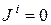 получаем, что
получаем, что 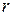 совпадает с индексом нильпотентности оператора
совпадает с индексом нильпотентности оператора  . Следовательно, матрица
. Следовательно, матрица 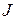 подобна
подобна

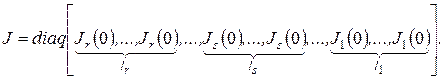
Очевидно, 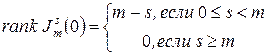 .
.
Тогда для 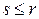
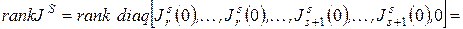
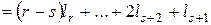 .
.
Если 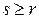 , то
, то 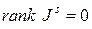 .
.
Значит,
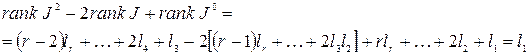 .
.
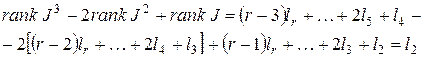
и т.д.
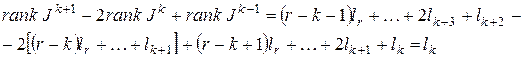
Равенства 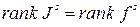 и
и 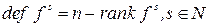 доказывают утверждение 2 и вместе с ним теорему.
доказывают утверждение 2 и вместе с ним теорему.
Следствие. Жорданова нормальная форма матрицы нильпотентного оператора определена однозначно с точностью до порядка следования диагональных клеток.
Обратимся к примеру, рассмотренному выше.
Так как индекс нильпотентности  равен
равен 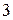 , то жорданова нормальная форма
, то жорданова нормальная форма 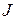 матрицы
матрицы 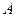 содержит по меньшей мере одну клетку Жордана порядка
содержит по меньшей мере одну клетку Жордана порядка 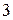 . В силу того, что порядок матрицы равен
. В силу того, что порядок матрицы равен 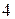 , такая клетка будет точно одна. Следовательно,
, такая клетка будет точно одна. Следовательно, 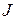 будет содержать еще одну клетку порядка I, т.е.
будет содержать еще одну клетку порядка I, т.е.
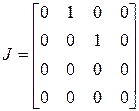 .
.
Если заранее известно, что  - матрица нильпотентного оператора (критерий нильпотентности оператора будет получен ниже) и неизвестен индекс нильпотентности, то можно использовать в решении утверждения I и 2 теоремы 2. В нашем случае имеем: число
- матрица нильпотентного оператора (критерий нильпотентности оператора будет получен ниже) и неизвестен индекс нильпотентности, то можно использовать в решении утверждения I и 2 теоремы 2. В нашем случае имеем: число 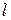 всех диагональных клеток матрицы
всех диагональных клеток матрицы 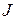 равно
равно 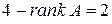 . Число
. Число 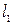 диагональных клеток первого порядка равно:
диагональных клеток первого порядка равно:
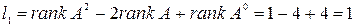 .
.
Следовательно, 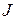 будет содержать еще одну клетку порядка 3, так как порядок матрицы
будет содержать еще одну клетку порядка 3, так как порядок матрицы  равен 4.
равен 4.
Замечание. Для 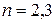 , достаточно знать количество клеток Жордана в жордановой нормальной форме, для
, достаточно знать количество клеток Жордана в жордановой нормальной форме, для 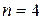 этого недостаточно только в случае, если количество клеток равно 2. В этой ситуации достаточно выяснить
этого недостаточно только в случае, если количество клеток равно 2. В этой ситуации достаточно выяснить 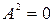 или нет: если
или нет: если 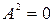 , то жорданова нормальная форма состоит из двух клеток второго порядка, если
, то жорданова нормальная форма состоит из двух клеток второго порядка, если 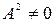 , то жорданова нормальная форма состоит из одной клетки первого порядка и одной — третьего.
, то жорданова нормальная форма состоит из одной клетки первого порядка и одной — третьего.
§ 3. Существование канонического базиса относительно произвольного линейного оператора.
Пусть  — линейный оператор
— линейный оператор 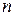 -мерного линейного пространства
-мерного линейного пространства 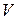 над полем
над полем 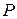 , а
, а 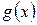 — полином над этим полем. Если
— полином над этим полем. Если 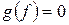 , то
, то 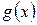 — называется аннулирующим линейный оператор
— называется аннулирующим линейный оператор  полиномом. Покажем, что существует аннулирующий оператор
полиномом. Покажем, что существует аннулирующий оператор  ненулевой полином. Так как пространство всех линейных операторов пространства
ненулевой полином. Так как пространство всех линейных операторов пространства 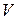 имеет размерность
имеет размерность 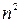 , то система
, то система 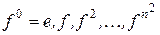 линейна зависима. Поэтому для некоторых элементов
линейна зависима. Поэтому для некоторых элементов 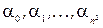 поля
поля 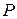 , не все из которых равны нулю
, не все из которых равны нулю
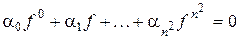 .
.
Тогда полином 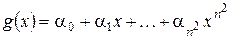 является ненулевым аннулирующим оператор
является ненулевым аннулирующим оператор  полиномом.
полиномом.
Например, характеристический полином линейного оператора, как будет показано ниже, является аннулирующим этот оператор полиномом (т. Гамильтона-Кэли).
Теорема 3. Пусть аннулирующий  полином
полином 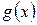 разлагается в произведение
разлагается в произведение 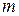 попарно взаимно простых множителей
попарно взаимно простых множителей
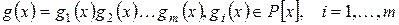 .
.
Тогда
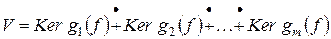 .
.
Доказательство проведем для случая 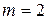 . В общем случае теорема доказывается аналогично.
. В общем случае теорема доказывается аналогично.
В силу взаимной простоты полиномов 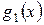 и
и 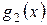 существуют в
существуют в 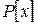 такие полиномы
такие полиномы 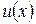 и
и 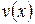 , что
, что
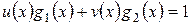 .
.
Тогда 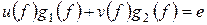 (1)
(1)
Далее, для любого 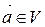 в силу (1) имеет место равенство
в силу (1) имеет место равенство
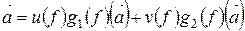 .
.
Покажем, что
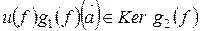 ,
,
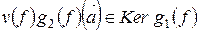 .
.
В самом деле,
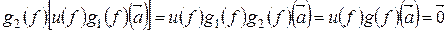
Аналогично 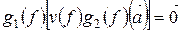 .
.
Тем самым доказано равенство
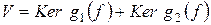 .
.
Если теперь 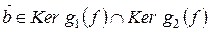 , то
, то 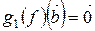 ,
, 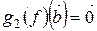 и, следовательно,
и, следовательно, 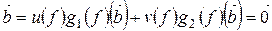 .
.
Теорема доказана.
Замечание. Легко убедиться, что подпространства 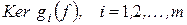 инвариантны относительно
инвариантны относительно 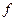 и ограничение
и ограничение 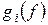 на
на 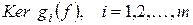 является нулевым оператором.
является нулевым оператором.
Пусть теперь аннулирующий 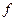 полином
полином 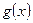 имеет вид
имеет вид
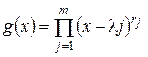 (2)
(2)
где 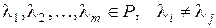 при
при 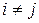 . Тогда по предыдущей теореме
. Тогда по предыдущей теореме
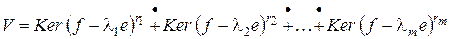 .
.
Как отмечено выше, подпространства 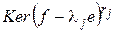 инвариантны относительно
инвариантны относительно  и ограничение
и ограничение 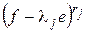 на
на 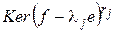 является нулевым оператором, т.е. ограничение
является нулевым оператором, т.е. ограничение 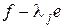 на
на 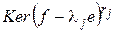 — нильпотентно
— нильпотентно 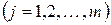 . В каждом ненулевом пространстве
. В каждом ненулевом пространстве 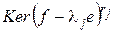 согласно теореме I можно выбрать канонический базис относительно ограничения
согласно теореме I можно выбрать канонический базис относительно ограничения 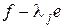 на
на 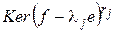 , в котором матрица этого ограничения имеет вид
, в котором матрица этого ограничения имеет вид
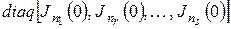
В этом же базисе матрица ограничения  на
на 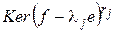 будет равна
будет равна 
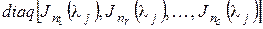 . Матрица линейного оператора
. Матрица линейного оператора  в базисе, который получается объединением всех канонических базисов, построенных в ненулевых подпространствах
в базисе, который получается объединением всех канонических базисов, построенных в ненулевых подпространствах
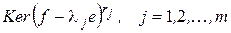 , приобретает вид
, приобретает вид 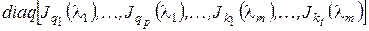 .
.
Тем самым теорема доказана.
Теорема 4. Относительно любого линейного оператора  пространства
пространства 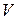 , аннулирующий полином которого имеет вид (2) (в частности, для любого линейного оператора конечномерного комплексного пространства) существует канонический базис.
, аннулирующий полином которого имеет вид (2) (в частности, для любого линейного оператора конечномерного комплексного пространства) существует канонический базис.
§ 4. Минимальный полином. Теорема Гамильтона-Кэли.
Пусть  линейный оператор пространства
линейный оператор пространства 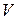 . Полином наименьшей степени среди аннулирующих
. Полином наименьшей степени среди аннулирующих  полиномов., старший коэффициент которого равен I, называется минимальным полиномом линейного оператора
полиномов., старший коэффициент которого равен I, называется минимальным полиномом линейного оператора  .
.
Пусть 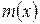 — минимальный полином
— минимальный полином 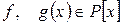 . Покажем, что полином
. Покажем, что полином 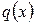 аннулирует
аннулирует  тогда и только тогда, когда он делится на
тогда и только тогда, когда он делится на 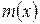 .
.
Представим 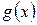 в виде
в виде
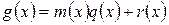 ,
,
где 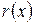 — остаток от деления
— остаток от деления 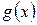 на
на 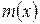 . Тогда
. Тогда
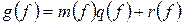 (I)
(I)
Так как 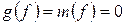 , то из равенства (I) следует
, то из равенства (I) следует 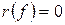 . Поэтому
. Поэтому 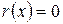 . Необходимость доказана.
. Необходимость доказана.
Достаточность очевидна.
Отсюда следует, что минимальный полином линейного оператора определен однозначно.
В самом деле, если 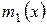 и
и 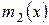 - минимальные полиномы линейного оператора, то в силу только что доказанного свойства они делят друг друга и, значит, совпадают.
- минимальные полиномы линейного оператора, то в силу только что доказанного свойства они делят друг друга и, значит, совпадают.
Приведем определение минимального полинома матрицы.
Пусть  - квадратная матрица над полем
- квадратная матрица над полем 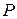 .
. 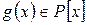 . Если
. Если 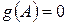 , то
, то 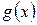 называется полиномом, аннулирующим матрицу
называется полиномом, аннулирующим матрицу  . Равенства
. Равенства 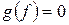 и
и 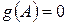 равносильны, если
равносильны, если  — линейный оператор с матрицей
— линейный оператор с матрицей  в некотором базисе. Поэтому существуют ненулевые полиномы, аннулирующие матрицу
в некотором базисе. Поэтому существуют ненулевые полиномы, аннулирующие матрицу  . Выберем среди них полином наименьшей степени со старшим коэффициентом I. Такой полином называется минимальным полиномом матрицы
. Выберем среди них полином наименьшей степени со старшим коэффициентом I. Такой полином называется минимальным полиномом матрицы  . Так как множество полиномов, аннулирующих матрицу
. Так как множество полиномов, аннулирующих матрицу  , совпадает с множеством полиномов, аннулирующих
, совпадает с множеством полиномов, аннулирующих  , то минимальный полином линейного оператора совпадает с минимальным полиномом его матрицы. Следовательно, минимальный полином матрицы обладает теми же свойствами, что и минимальный полином линейного оператора, а также минимальные полиномы подобных матриц равны.
, то минимальный полином линейного оператора совпадает с минимальным полиномом его матрицы. Следовательно, минимальный полином матрицы обладает теми же свойствами, что и минимальный полином линейного оператора, а также минимальные полиномы подобных матриц равны.
 2015-09-06
2015-09-06 1188
1188