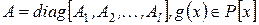Доказательство. Пусть

.

Тогда

.

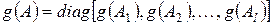Следовательно, полином 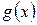аннулирует матрицу тогда и только тогда, когда он аннулирует каждую ее клетку , т.е. является общим кратным минимальных полиномов этих клеток. Поэтому минимальный полином матрицы будет равен НОК минимальных полиномов ее диагональных клеток.

Упражнение. Пусть - квадратная матрица над полем 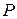. Очевидно, множество 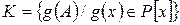является кольцом относительно обычных операций сложения и умножения матриц. Найти необходимое и достаточное условие, чтобы кольцо 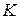являлось полем.

Теорема 6. (Гамильтона-Кэли).

Квадратная матрица является корнем своего характеристического полинома.

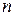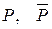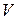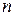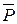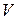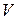Доказательство. Пусть — квадратная матрица порядка над полем — поле, которому принадлежат все корни ненулевого аннулирующего матрицу полинома, — -мерное линейное пространство над полем . Выберем в базис и рассмотрим линейный оператор пространства с матрицей в отмеченном базисе. В силу теоремы 4 существует канонический базис относительно . Пусть 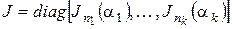матрица в этом базисе. Так как характеристические и минимальные полиномы подобных матриц равны, то характеристический полином матрицы равен произведению характеристических полиномов диагональных клеток матрицы , а минимальный полином матрицы равен НОК этих же полиномов в силу предыдущей теоремы и того, что минимальный полином клетки Жордана совпадает с ее характеристическим полиномом. Следовательно, .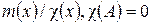

Следствие. (Критерий нильпотентности оператора). Линейный оператор 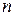- мерного линейного пространства нильпотентен тогда и только тогда, когда его характеристический полином равен .

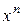Доказательство. Необходимость.

Пусть — нильпотентный оператор 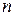-мерного векторного пространства ,

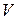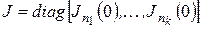- матрица в каноническом базисе. Очевидно, ее характеристический полином равен .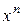

Достаточность вытекает из теоремы Гамильтона-Кэли.

Ответ на поставленную в § I задачу дает теперь следующая

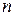Теорема 7. Пусть — линейный оператор -мерного линейного пространства над полем 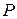. Существует канонический базис относительно тогда и только тогда, когда все корни характеристического полинома оператора принадлежат полю .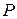

Доказательство. Необходимость.

Пусть 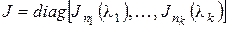- матрица в каноническом базисе. Тогда 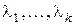принадлежат полю 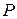, характеристический полином оператора равен .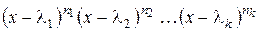

Достаточность следует из теоремы Гамильтона-Кэли и теоремы 4.

Заметим, что способ построения канонического базиса относительно содержится в доказательстве теоремы 4 (в качестве аннулирующего полинома нужно брать его характеристический полином).

Упражнение. Сформулировать аналогичную теорему на матричном языке.

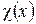Получим теперь алгоритм построения жордановой нормальной формы матрицы линейного оператора , не находя канонического базиса относительно . Пусть характеристический полином оператора равен

,

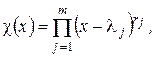где 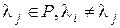при 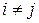. Для решения нашей задачи достаточно знать количество 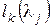клеток Жордана порядка 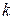с элементом 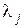на диагонали 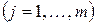. Как следует из доказательства теоремы 4, 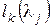равно количеству клеток порядка 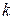в жордановой нормальной форме ограничения 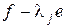на 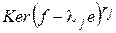. Так как в жордановой нормальной форме матрицы оператора на диагонали стоят собственные значения этого оператора, причем каждое собственное значение встречается столько раз, какова его кратность, то 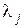встречается на диагонали точно 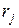раз, т.е. 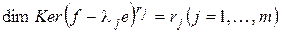и, следовательно, клеток Жордана порядка 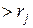не будет. Покажем, что для любог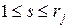о ядро 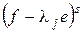совпадает с ядром ограничения 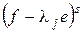на 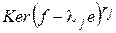. Это следует из очевидного включения 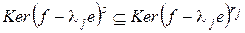. Значит, дефект 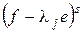совпадает с дефектом ограничения 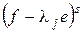на 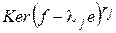. Далее в силу нильпотентности ограничения 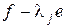на подпространство 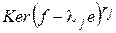и теоремы 2

(*)

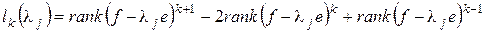По тем же причинам количество 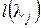всех клеток Жордана с элементом 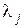на диагонали равно дефекту 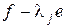или 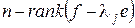. Т.е.

. (**)

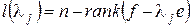Поскольку 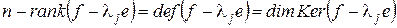, то 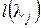равно максимальному числу линейно независимых собственных векторов оператора , соответствующих собственному значению .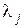

Подпространство 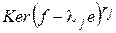называется корневым подпространством, соответствующим собственному значению 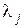оператора . Из только что приведенных рассуждений в силу независимости ранга матрицы линейного оператора от выбора базиса следует, что жорданова нормальная форма матрицы определена однозначно с точностью до расположения клеток на “диагонали”.

Если 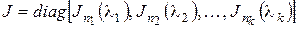— жорданова нормальная форма матрицы , то система полиномов 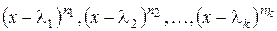называется системой элементарных делителей матрицы (или 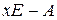). В силу формулы (*) система элементарных делителей матрицы определена однозначно с точностью до порядка их записи. Из предыдущей теоремы следует

Критерий подобия матриц над .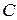

Две матрицы подобны над тогда и только тогда, когда совпадают системы их элементарных делителей.

Прежде, чем обратиться к примерам, выделим алгоритм построения жордановой нормальной формы 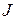матрицы.

1. Находим характеристический многочлен 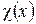матрицы и его корни. Если не все корни полинома 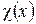принадлежат основному полю, то жордановой нормальной формы над этим полем не существует.

2. Пусть все корни полинома 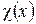принадлежат основному полю, 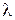- один из них. Пользуясь формулами (*) и (**) этого параграфа, находим все клетки Жордана матрицы 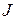с элементом 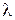на диагонали.

3. Переходим к следующему корню, с ним поступаем так же, как и с 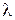. Процесс заканчивается, когда переберем все различные корни полинома.

4. Из всех полученных клеток Жордана составляем квазидиагональную матрицу. Эта матрица — искомая.

Замечание. Если кратность некоторого корня 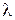полинома 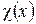не выше 3, то для отыскания всех клеток Жордана с элементом 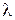на диагонали достаточно вычислить лишь 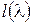по формуле (**).