Лейбниц формуласы

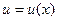Егер және 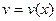функцияларының 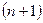-ші ретке дейінгі туындылары бар болса, онда

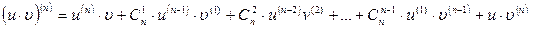(14)

формуласы орынды болады. Мұнда 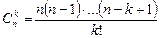биномдық коэффициенттер. (14) формуланы Лейбниц формуласы деп атайды.

Егер көбейтіліп тұрған функциялардың біреуінің туындылары белгілі бір реттен бастап нөлге айналып, екіншісінің туындылары оңай табылса, онда Лейбниц формуласын қолдану нәтижелі болады.

Мысалы, 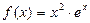функциясының 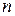-шіретті туындысын табайық.

Шешуі. Егер 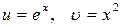болса, онда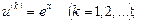 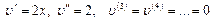болады. Демек, (4.14) бойынша

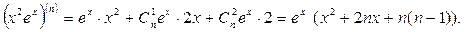
Параметр арқылы берілген функцияның жоғары ретті туындылары

Параметр арқылы берілген 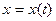, 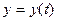функцияны қарастырайық. Оның бірінші ретті туындысы 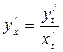формуласымен анықталатындығы белгілі. Екінші ретті 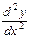туындысын, 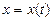, 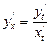параметр арқылы берілген функцияның туындысы ретінде анықтау керек. Сонда, бірінші ретті туындыны анықтау формуласын және бөлшектің туындысын табу ережесін пайдалансақ, келесі формуланы аламыз:

.

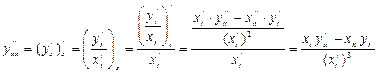Мысалы, 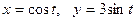функциясының екінші ретті туындысын табайық.

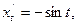
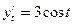болғандықтан . .

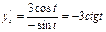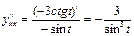7. Дифференциалдық есептеудің негізгі теоремалары

Локальді экстремум. Егер 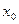нүктесінің 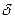- маңайында функцияның қабылдаған мәндері сол нүктедегі мәнінен аспаса (кем болмаса), онда 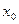-ді сол функцияның локальді максимум (локальді минимум) нүктесі деп атайды. Сонымен 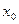нүктесі 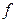функциясының локальді максимум (локальді минимум) нүктесі болуы үшін 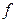функциясы 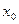нүктесінің белгілі бір 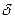маңайында анықталып

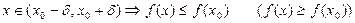. (4.15)

шарты орындалуы керек. Кейде (4.15) шарты

.

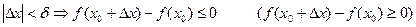түрінде қолданылады.

Егер 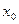локальді максимум немесе локальді минимум нүктесі болса, онда оны локальді экстремум нүктесі деп атайды.

6-теорема (Ферма теоремасы). Егер функциясы үшін х _о локальді экстремум нүктесі болып, сол нүктеде 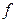-тің ақырлы туындысы бар болса, онда сол туындының мәні нөлге тең болады.

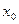Ескертулер. 1. Экстремумның анықтамасындағы шарт функциясының нүктесінің екі жақты маңайында орындалуы дифференциалдау теориясын пайдалану үшін қажет.

2. Кері тұжырым дұрыс емес, яғни 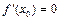болса да, 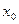нүктесі экстремум нүктесі болмауы мүмкін.

Мысалы, 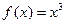үшін 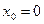болғанда 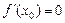, бірақ 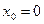экстремум нүктесі емес

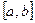4.7-теорема (Ролль теоремасы). функциясы сегментінде анықталып, келесі шарттар орындалсын:

1) 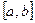сегментінде үзіліссіз,

2) 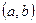интервалында дифференциалдансын,

3) 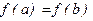болсын.

Онда 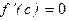шартын қанағаттандыратын кемінде бір 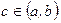нүктесі табылады.

4.8-теорема (Лагранж теоремасы). Егер функциясы 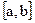сегментінде үзіліссіз болып, 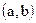интервалында дифференциалданса, онда

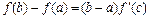(4.16)

теңдігі орындалатын кемінде бір 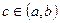нүктесі табылады.

(4.16) - формуланы Лагранж формуласы немесе ақырлы өсімшелер формуласы деп те атайды.

4.9-теорема (Коши теоремасы). Егер және 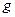функциялары 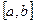сегментінде үзіліссіз болып, 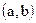интервалында дифференциалданса, онда

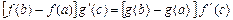. (4.17)

теңдігі орындалатын кемінде бір 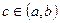нүктесі бар болады.