Система лінійних алгебраїчних рівнянь має вигляд:
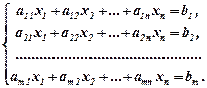 (1)
(1)
Числа 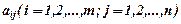 - коефіцієнти біля невідо-
- коефіцієнти біля невідо-
мих 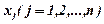 , а
, а 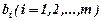 - вільні члени.
- вільні члени.
Розв’язком системи (1) називається сукупність чисел 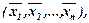

 яка при підстановці її в систему перетворює всі рівняння в правильні рівності (тотожності).
яка при підстановці її в систему перетворює всі рівняння в правильні рівності (тотожності).
Якщо число рівнянь 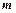 дорівнює числу невідомих
дорівнює числу невідомих 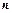 то для розв’язування системи рівнянь можна використати:
то для розв’язування системи рівнянь можна використати:
а) правило Крамера. Якщо основний визначник 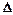 системи
системи 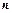 лінійних алгебраїчних рівнянь з
лінійних алгебраїчних рівнянь з 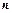 невідомими (визначник складений із коефіцієнтів, що стоять біля невідомих) не дорівнює нулю, то ця система має єдиний розв’язок, який знаходиться за формулами:
невідомими (визначник складений із коефіцієнтів, що стоять біля невідомих) не дорівнює нулю, то ця система має єдиний розв’язок, який знаходиться за формулами:
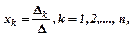
де 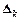 -допоміжний визначник, який одержується з основного визначника
-допоміжний визначник, який одержується з основного визначника 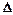 шляхом заміни його
шляхом заміни його 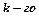 стовпчика стовпчиком вільних членів системи.
стовпчика стовпчиком вільних членів системи.
б) матричний метод. У матричній формі систему лінійних рівнянь запишемо так 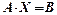 . Звідси розв’язок:
. Звідси розв’язок: 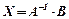 .
.
Для довільних систем, лінійних алгебраїчних рівнянь використовують методи Гаусса, Жордана –Гаусса.
в) метод Гаусса полягає в послідовному виключенні невідомих з рівнянь системи і зведенні її до трикутного чи трапецевидного вигляду.
г) метод Жордана - Гаусса полягає в повному послідовному виключенні невідомих. При цьому коефіцієнти утворять при основних (базисних) невідомих одиничну матрицю.
4. Елементи аналітичної геометрії і векторної алгебри.
Дві взаємно перпендикулярні осі Ох і Оу з спільною точкою початку відліку О і однаковою масштабною одиницею утворюють декартову систему координат на площині.
Точка на площині задається впорядкованою парою чисел (х,у), які називають координатами.
Віддаль d між точками А (x1, y1) іB (x2, y2) обчислюється за формулою: d = 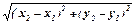 .
.
Координати точки С (x, y), яка ділить відрізок АВ у відношенні АС:СВ=l, знаходяться за формулами: 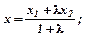
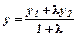 .
.
В просторі три взаємно перпендикулярні осі Ох, Оу,Оz з спільною точкою відліку О і однаковою масштабною одиницею утворюють декартову систему координат.Точка в просторі задається впорядкованою трійкою чисел – координатами (х,у,z).
Направлений відрізок 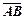 , де точка А точка початку,а В точка кінця називається вектором.
, де точка А точка початку,а В точка кінця називається вектором.
Вектор позначається або двома великими буквами з стрілкою над ними 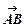 ,або одною малою буквою
,або одною малою буквою 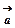 . Довжину вектора називають модулем і позначають
. Довжину вектора називають модулем і позначають 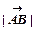 або
або 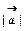 .
.
Вектор на площині задають двома числами його координатами: 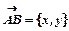 ,де
,де 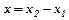 ,
, 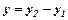 , які є проекціями вектора відповідно на осі Ох та Оу. Вектор в просторі задають трьома координатами:
, які є проекціями вектора відповідно на осі Ох та Оу. Вектор в просторі задають трьома координатами: 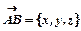 .
.
Сумою(різницею) двох векторів 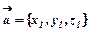 і
і 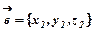 називають вектор
називають вектор 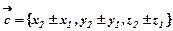 .
.
Скалярним добутком векторів 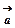 і
і 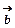 називають вектор
називають вектор 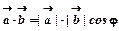 , де
, де 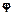 - кут між векторами.
- кут між векторами.
Якщо вектори задані своїми координатами, то 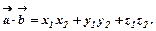
Кут 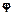 між векторами обчислюється за формулою:
між векторами обчислюється за формулою:
cosj = 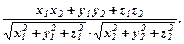
Умова паралельності векторів: 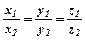 .
.
Умова перпендикулярності векторів: 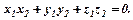
5. П ряма на площині
1. Рівняння прямої з кутовим коефіцієнтом: y = kx + b, де 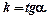 (
(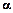 - кут нахилу прямої до додатнього напряму осі
- кут нахилу прямої до додатнього напряму осі 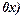 , b - довжина відрізка, який пряма відтинає на осі Oy.
, b - довжина відрізка, який пряма відтинає на осі Oy.
2. Рівняння в’язки прямих, що проходять через точку 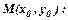
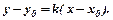
3. Рівняння прямої, що проходить через дві точки 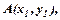
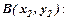
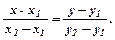
4. Рівняння прямої у відрізках на осях: 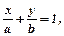 де
де 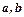 - відрізки, які пряма відсікає на осях координат.
- відрізки, які пряма відсікає на осях координат.
5.Загальне рівняння прямої: Ax + By + C = 0.
Кут 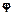 , відрахований проти годинникової стрілки від прямої
, відрахований проти годинникової стрілки від прямої
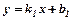 до прямої
до прямої 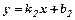 знаходиться за формулою:
знаходиться за формулою:

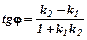 .
.
Умова паралельності цих прямих: 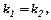
Умова перпендикулярності: 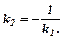
Віддаль 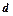 точки
точки 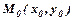 від прямої
від прямої 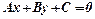 обчислюємо за формулою:
обчислюємо за формулою:
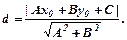
 2015-09-06
2015-09-06 249
249








