Похідною функції у=f(x) в точці x називається границя відношення приросту функції ∆ у до приросту аргументу ∆х в цій точці,
коли ∆х →0
Позначають похідну 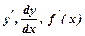 .
.
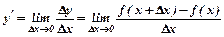 .
.
Якщо ця границя скінченна, то функція називається диференційованою в т. 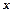 . Основні правила і формули диференціювання поміщені в таблиці:
. Основні правила і формули диференціювання поміщені в таблиці:
| ОСНОВНІ ФОРМУЛИ ДИФЕРЕНЦІЮВАННЯ | |||
| y = C | y' = 0 | y = x | y' = 1 |
| y = Cu | y' = Cu' | y = u 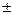 v v
| y' = u' 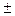 v' v'
|
| y = uv | y' = u'v +v'u | 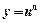
| 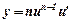
|
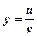
| 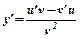
| 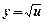
| 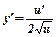
|
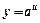
| 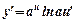
| 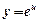
| 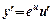
|
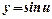
| y ΄= cosu u΄ | 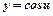
| y ΄= - sinu u ΄ |
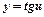
| 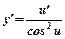
| 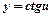
| 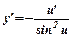
|
| 
| 
| 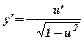
|
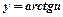
| 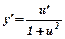
| 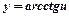
| 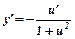
|
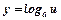
| 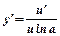
| 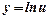
| 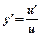
|
| y=f(u), u=j(x) | 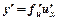
| x = j(y) обернена до y=f(x) | 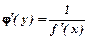
|
Диференціал функції 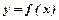 обчислюється за формулою:
обчислюється за формулою:
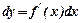 .
.
 2015-09-06
2015-09-06 396
396








