Якщо кожному значенні змінної 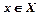 поставлено у відповідність за певним правилом значення
поставлено у відповідність за певним правилом значення 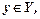 то говорять, що задана функція. Її позначають
то говорять, що задана функція. Її позначають 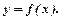
Множина Х називається областю визначення функції, множина 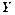 - областю значень функції.
- областю значень функції.
Множина значень 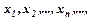 яка за певним правилом поставлена у відповідність натуральному ряду чисел
яка за певним правилом поставлена у відповідність натуральному ряду чисел 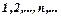 називається числовою послідовністю.
називається числовою послідовністю.
Числа 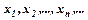 називають членами послідовності, при цьому
називають членами послідовності, при цьому 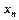 - загальним членом.
- загальним членом.
Число 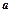 називається границею послідовності
називається границею послідовності 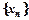 , якщо для всякого як завгодно малого додатнього числа
, якщо для всякого як завгодно малого додатнього числа 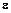 знайдеться такий номер
знайдеться такий номер 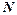 , що для всіх
, що для всіх 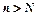 виконується нерівність
виконується нерівність 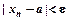 . Це позначають
. Це позначають 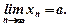
Якщо послідовність має скінчену границю, то її називають збіжною.
Важливим прикладом числової послідовності є геометрична прогресія.
Послідовність чисел називається геометричною прогресією, якщо кожний наступний її член дорівнює попередньому помноженому на деяке стале число 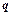 - знаменник прогресії:
- знаменник прогресії: 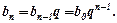
Число 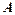 називається границею функції
називається границею функції 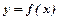 в точці
в точці 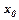 , якщо для будь-якої збіжної до
, якщо для будь-якої збіжної до 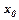 послідовності значень аргументу
послідовності значень аргументу 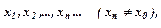 відповідна послідовність значень функції
відповідна послідовність значень функції 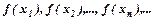 збіжна до
збіжна до 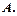 Це записують
Це записують 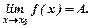
Основні теореми про границі функцій:
1. Границя сталої дорівнює цій сталій.
2. Границя алгебраїчної суми, добутку, частки двох функцій
дорівнює відповідно алгебраїчній сумі, добутку та частці їх границь при умові, що границя функції в знаменнику не дорівнює 0.
Випадки, коли не можна знайти границі безпосередньо за цими теоремами, це невизначеності: 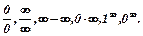 Для розкриття невизначеностей використовують визначні границі:
Для розкриття невизначеностей використовують визначні границі:
1. 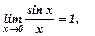
2. 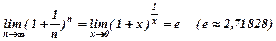 .
.
В фінансових розрахунках використовують формули нагромадження капіталу за складними відсотками знайдені на основі геометричної прогресії: 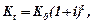 де
де  - сума вкладу нагромадження через
- сума вкладу нагромадження через  років,
років,  - початкова сума вкладу,
- початкова сума вкладу, 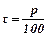 - коефіцієнт складних відсотків при
- коефіцієнт складних відсотків при 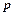 - щорічному відсотковому приросту.
- щорічному відсотковому приросту.
Якщо відсотки нараховуються 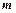 разів за рік, то
разів за рік, то 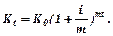
Якщо зростання за складними відсотками неперервне, то на основі другої визначної границі формула набуде вигляду 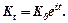
 2015-09-06
2015-09-06 369
369








