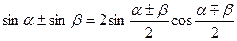 ;
; 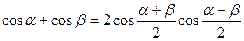
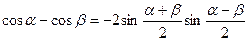 ;
; 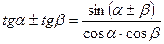
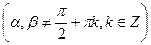 ;
;
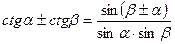
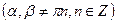 .
.
Формулы преобразования произведения тригонометрических функций в сумму (разность).
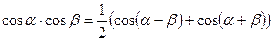 ;
; 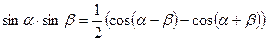
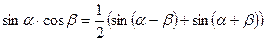
Функции обратные тригонометрическим.
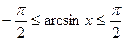 ,
, 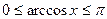 ,
, 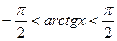 ,
, 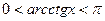
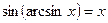 и
и 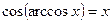 , если
, если 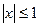

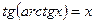 и
и 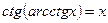 , если
, если 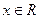 .
.
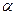
| 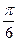
| 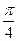
| 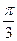
| 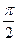
| 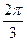
| 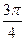
| 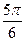
| 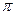
| |
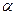
| 0 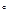
| ||||||||
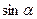
| 
| 
| 
| 
| 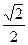
| 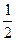
| |||
 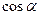
| 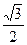
| 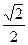
| 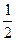
| 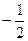
| 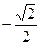
| 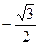
| -1 | ||
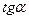
| 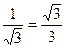
| 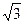
| - | 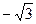
| - 1 | 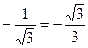
| |||
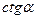
| - | 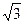
| 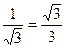
| 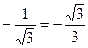
| -1 | 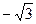
| - |
Формулы корней тригонометрических функций.
cos t = 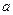 ,
, 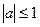 t =
t = 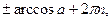 n
n 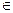 Z;
Z;
Если cos t = 0, то 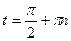 ,
, 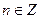 ; если cos t = 1, то
; если cos t = 1, то 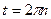 ,
, 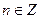 ;
;
если cos t = ─ 1, то t = 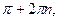
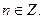
sin t = a, 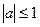 t =
t = 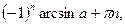 n
n 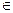 Z;
Z;
Если sin t = – 1, то t = − 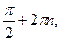 n
n 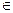 Z; если sin t = 0, то t =
Z; если sin t = 0, то t = 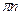 ,
, 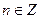 ;
;
если sin t = 1, то t = 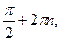
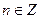 .
.
tg t = a, t = arctg a + 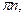 n
n 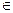 Z; ctg t = a, t = arcctg a +
Z; ctg t = a, t = arcctg a + 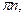
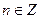 .
.
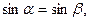
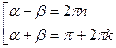
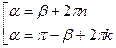
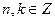 ;
; 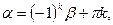
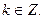
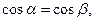
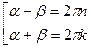
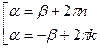
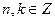 ;
; 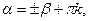
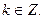
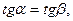
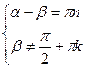

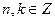 ;
;
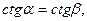
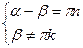
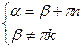
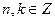 .
.
Решение тригонометрических неравенств.
· sin x > a, 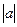 < 1 x
< 1 x 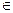 (arcsin a + 2k
(arcsin a + 2k 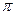 ;
; 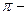 arcsin a + 2k
arcsin a + 2k 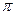 ), k
), k 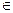 Z;
Z;
· sin x < a, 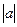 < 1 x
< 1 x 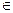 (
(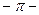 arcsin a + 2k
arcsin a + 2k 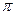 ; arcsin a + 2k
; arcsin a + 2k 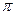 ), k
), k 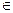 Z;
Z;
· cos x > a, 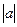 < 1 x
< 1 x 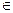 (−arccos a + 2k
(−arccos a + 2k 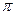 ; arccos a + 2k
; arccos a + 2k 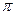 ), k
), k 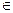 Z;
Z;
· sin x < a, 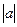 < 1 x
< 1 x 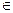 (arccos a + 2k
(arccos a + 2k 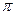 ; 2
; 2 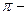 arcsin a + 2k
arcsin a + 2k 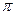 ), k
), k 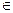 Z;
Z;
· tg x > a x 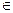 (arctg a +k
(arctg a +k 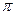 ;
; 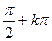 ), k
), k 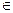 Z;
Z;
· tg x < a x 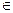 (
(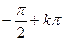 ; arctg a + k
; arctg a + k 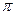 ), k
), k 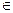 Z;
Z;
· ctgx> a x 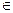 (
(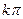 ; arcctg a +k
; arcctg a +k 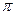 ), k
), k 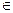 Z;
Z;
· ctg x < a x 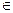 (arcctg a + k
(arcctg a + k 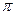 ;
; 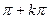 ), k
), k 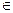 Z.
Z.
 2015-09-06
2015-09-06 515
515








