Диференцiальне рівняння
M(x, y)dx + N(x, y)dy = 0 (1)
називають рiвнянням у повних диференцiалах, якщо йоголiва частина є повним диференцiалом деякої функцiї U(x, y),тобто
M(x, y)dx + N(x, y)dy = dU(x, y). (2)
З (1), (2) випливає, що рiвняння (1) можна записатиу виглядi dU = 0, а тому загальним iнтегралом рiвняння уповних диференцiалах є U(x, y) = C.
Критерієм того, що рівняння є рівнянням в повних диференціалах, тобто необхідною та достатньою умовою, є виконання рівності
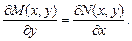
В деяких випадках рівняння
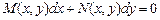
не є рівнянням в повних диференціалах, але існує функція 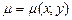 така, що рівняння
така, що рівняння
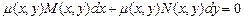 вже буде рівнянням в повних диференціалах. Необхідною та достатньою умовою цього є рівність
вже буде рівнянням в повних диференціалах. Необхідною та достатньою умовою цього є рівність
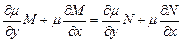 .
.
Таким чином замість звичайного диференціального рівняння відносно функції 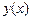 одержимо диференціальне рівняння в частинних похідних відносно функції
одержимо диференціальне рівняння в частинних похідних відносно функції 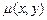 . Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію
. Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію 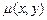 , наприклад
, наприклад  де
де 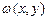 - відома функція. В цьому випадку одержуємо
- відома функція. В цьому випадку одержуємо
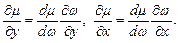
Після підстановки в рівняння маємо
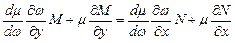 Розділимо змінні
Розділимо змінні
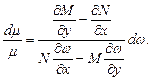
Проінтегрувавши і поклавши сталу інтегрування одиницею, одержимо:
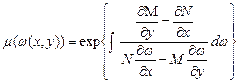
 2015-09-06
2015-09-06 1445
1445








