Теорема (про неперервну залежнiсть розв’язкiввiд параметру). Якщо права частина диференцiального рiвняння
yl= f(x, y, μ) неперервна за змiнною μ, μ ∈ [μ1, μ2], i для кожногофiксованого μ задовольняє умови теореми 2 з тими самими сталимиa, b, L, M, то розв’язок
y = y(x, μ) рiвняння (6.11), який задовольняє початкову умову y(x0) = y0, неперервно залежитьвiд μ.
Теорема (про неперервну залежнiсть вiд початкових умов). Нехай виконанi умови теореми 2. Тодi розв’язокзадачi Кошi
y = y(x, x0, y0) неперервно залежить
вiд початкових умов.
Особливі точки та лінії для рівняння y'=f(x, y).
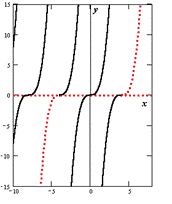
Якщо в околі точки (x0, y0) площині для рівняння y'=f(x,y) виконуються умови існування та єдиності розв'язку задачі Коші (безперервність f(x, y) і f'y (x, y)), то через цю точку проходить єдина інтегральна крива. Якщо ці умови порушуються, точку (x0, y0) називають особливою точкою диференціального рівняння. Через особливу точку може не проходити жодної інтегральної кривої (тобто задача y'=f(x, y), y (x0) = y0 не має рішення); може проходила одна інтегральна крива; може проходити декілька інтегральних кривих. Особливі точки можуть утворити криву, яка сама є інтегральною кривою рівняння. Рішення рівняння, в кожній точці якого порушується його єдиність, називають особливим рішенням. Для прикладу розглянемо рівняння y'=3y2/3. Тут f(x,y)=3y2/3 - неперервна в будь-якій точці (x,y), але - не має кінцевого межі при, тобто в будь-якій точці (x,y) при y=0 порушується умова існування безперервної похідної. Отже, будь-яка точка (x,0) є особливою точкою рівняння. Пряма y=0, очевидно, інтегральна крива рівняння (функція y=0 задовольняє рівнянню). Знайдемо спільне рішення цього рівняння:
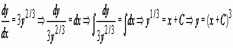
 2015-09-06
2015-09-06 496
496








