Лінійні диференціальні рівняння та рівняння, що зводяться до них. Методи Лагранжа та Бернуллі

Лінійним рівнянням першого порядку називають рівняння, у яке шукана функція та її похідна входять у першому степеніі не перемножуються. Отже, лінійне рівняння має такий загальний вигляд:

A(x)y^l + B(x)y + C(x) = 0, (1)

де A(x), B(x), C(x) – неперервні функції. В області, де A(x) = 0, рівняння (1) рівносильне рівнянню

y^l+ p(x)y = q(x), (2)

у якому позначено

p(x) = B(x)/A(x), q(x) = −C(x)/A(x).

Якщо функція q(x) тотожно дорівнює нулю, то рівняння (2) називають лінійним однорідним, а якщо тотожно не дорівнює нулю, то лінійним неоднорідним.

рівнює нулю, то лінійним неоднорідним.

Метод Лагранжа (метод варіації довільної сталої) використається для розв’язування лінійних рівнянь першого порядку.

лінійне однорідне рівняння

y^l + p(x)y = 0, яке є водночас рівнянням з відокремлюваними змінними:

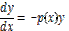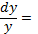⇒ − p(x)dx (y = 0) ⇒

ln |y| = − ⇒ y = Ce−p(x)dx. (3)

Розв’язок лінійного неоднорідного рівняння (2) шукатимемо у вигляді (3), замінивши довільну сталу C деякою функцією C(x), тобто у вигляді

y = C(x)e^−p(x)dx. (4)

Підставляючи (4) у рівняння (2), одержуємо

C^l(x)e^−∫p(x)dx− C(x)p(x)e^−∫p(x)dx + p(x)C(x)e^−∫p(x)dx = q(x) ⇒Cl(x) = q(x)e∫ p(x)dx⇒ C(x) =∫q(x)e∫p(x)dx dx + C,

де C – довільна стала.

Підставляючи тепер знайдену функцію C(x) у (4), маємоформулу для загального розв’язку лінійного рівняння (2):

y = e^∫−p(x)dx ·(∫q(x)e^∫p(x)dxdx + C). (5)

Рівняння вигляду y^l+ p(x)y = q(x)y^m, (6)

де m – деяке число, називають рівнянням Бернуллі. Якщо m = 0, то одержуємо лінійне неоднорідне рівняння (2), а якщо m = 1, то рівняння з відокремлюваними змінними y^l + (p(x) − q(x))y = 0, тому надалі вважатимемо, що m ≠ 0, m ≠ 1.

Для розв’язування рівняння Бернуллі, так само, як лінійного рівняння, використаємо метод варіації довільної сталої.