Рассмотрим теперь случай, когда энергия частицы может принимать любые непрерывные значения. Это имеет место, например, в случае поступательного движения молекул газа или когда, в соответствии с (3.1), расстояние между уровнями энергии частицы мало по сравнению с ее средней тепловой энергией. В этом случае определяют вероятность того, что частица обладает каким-либо значением энергии в интервале от 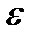 до
до 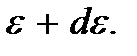 В этом квазиклассическом случае величина
В этом квазиклассическом случае величина 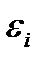 заменяется на кинетическую энергию частицы, а кратность вырождения уровня
заменяется на кинетическую энергию частицы, а кратность вырождения уровня 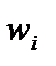 - на число состояний dw (ε), соответствующих интервалу энергий от
- на число состояний dw (ε), соответствующих интервалу энергий от 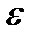 до
до 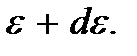 Учитывая, что это число состояний dw (ε) ~
Учитывая, что это число состояний dw (ε) ~ 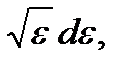 будем иметь
будем иметь
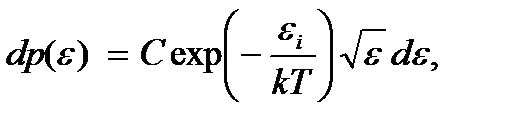
где C – постоянный коэффициент пропорциональности. Введем функцию 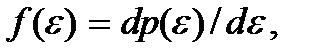 определяющую плотность вероятности обнаружить частицу в состоянии с каким-либо значением энергии в интервале от
определяющую плотность вероятности обнаружить частицу в состоянии с каким-либо значением энергии в интервале от 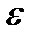 до
до 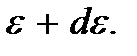 Тогда
Тогда

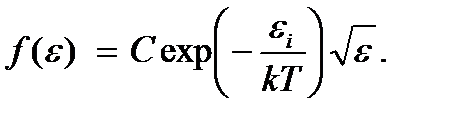
Постоянная С определяется условием нормировки
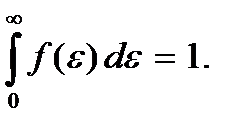
Поскольку
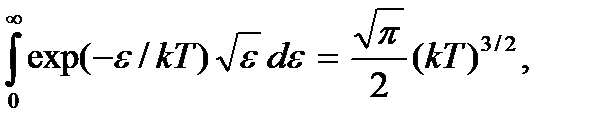
будем иметь
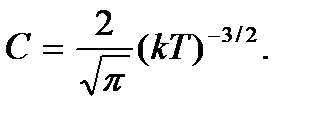
Тогда искомая вероятность того, что частица обладает каким-либо значением энергии в интервале от 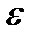 до
до 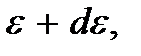 определится как
определится как
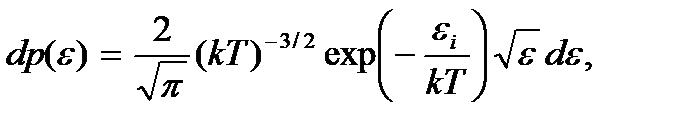 (3.12)
(3.12)
а плотность этой вероятности
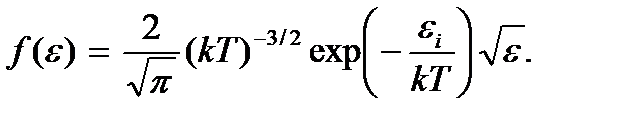 (3.13)
(3.13)
Умножив вероятность (3.12) на число молекул газа N, можно определить число молекул, обладающих энергией, заключенной в интервале от 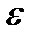 до
до 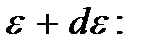
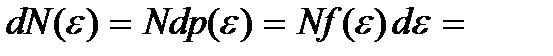
= 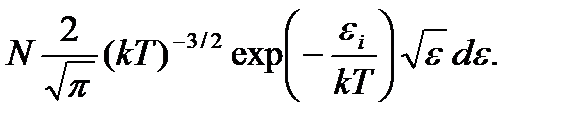 (3.14)
(3.14)
Соотношение (3.14) называют распределением Максвелла –Больцмана по кинетической энергии частиц, а функцию 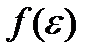 – функцией распределения Максвелла – Больцмана по кинетической энергии частиц График этой функции для двух значений температур T 1 и
– функцией распределения Максвелла – Больцмана по кинетической энергии частиц График этой функции для двух значений температур T 1 и 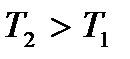 показан на рис. 3.3. Наличие двух конкурирующих множителей – монотонно возрастающего
показан на рис. 3.3. Наличие двух конкурирующих множителей – монотонно возрастающего 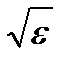 и монотонно убывающего
и монотонно убывающего 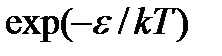 – обусловливает существование у функции
– обусловливает существование у функции 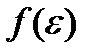 максимума при некотором значении ε = εв. Этой энергией обладает наибольшее число молекул газа, поэтому ее называют наиболее вероятной кинетической энергией. Ее можно найти из условия максимума функции
максимума при некотором значении ε = εв. Этой энергией обладает наибольшее число молекул газа, поэтому ее называют наиболее вероятной кинетической энергией. Ее можно найти из условия максимума функции 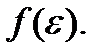 Получим
Получим 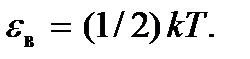 Видим, что с увеличением температуры эта наиболее вероятная кинетическая энергия возрастает, а максимум кривой распределения смещается в сторону больших энергий. Молекулам становятся доступными большие значения кинетической энергии. Из рис. 3.3. видно, что кривая
Видим, что с увеличением температуры эта наиболее вероятная кинетическая энергия возрастает, а максимум кривой распределения смещается в сторону больших энергий. Молекулам становятся доступными большие значения кинетической энергии. Из рис. 3.3. видно, что кривая 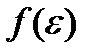 , соответствующая более высокой температуре T 2, в области малых значений энергии лежит ниже той же кривой, соответствующей более низкой температуре
, соответствующая более высокой температуре T 2, в области малых значений энергии лежит ниже той же кривой, соответствующей более низкой температуре 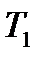 , а в области больших значений энергии – выше. Это означает, что с повышением температуры газа вероятность обнаружить молекулу с большим значением кинетической энергии становится больше вероятности обнаружить молекулу с малым значением кинетической энергии. Число молекул с малым значением кинетической энергии уменьшается, а число молекул с большим значением кинетической энергии возрастает. Происходит перераспределение молекул по энергиям. В этом и состоит процесс нагревания газа.
, а в области больших значений энергии – выше. Это означает, что с повышением температуры газа вероятность обнаружить молекулу с большим значением кинетической энергии становится больше вероятности обнаружить молекулу с малым значением кинетической энергии. Число молекул с малым значением кинетической энергии уменьшается, а число молекул с большим значением кинетической энергии возрастает. Происходит перераспределение молекул по энергиям. В этом и состоит процесс нагревания газа.
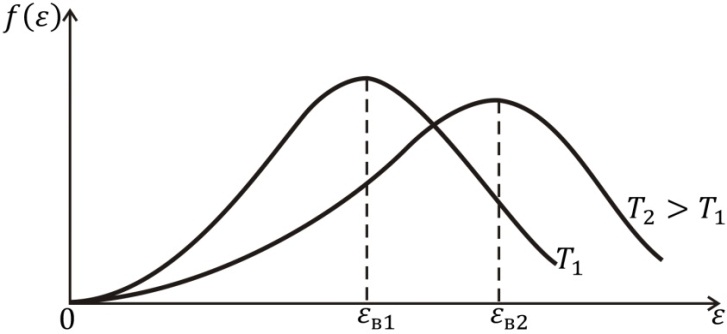
Рис. 3.3
Площадь под кривой 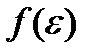 от температуры не зависит и в соответствии с условием нормировки функции
от температуры не зависит и в соответствии с условием нормировки функции 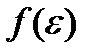 равна единице.
равна единице.
Зная функцию распределения 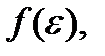 можно найти среднее значение кинетической энергии. Как легко убедиться,
можно найти среднее значение кинетической энергии. Как легко убедиться,
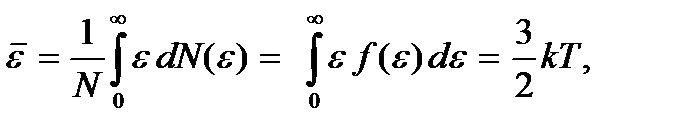
что совпадает с ранее полученным значением. Так и должно быть, ибо выбор β в виде 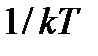 определялся именно этим обстоятельством.
определялся именно этим обстоятельством.
 2015-09-06
2015-09-06 599
599








