2015-09-06
780
Пусть имеется система N не взаимодействующих между собой частиц (идеальный газ);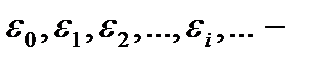 
совокупность возможных значений (уровней) энергии частицы. Дискретными значениями энергии обладают, например, вращательное и колебательное движения молекул. Ставится задача: определить вероятность 
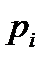того, что какая-либо частица обладает энергией 
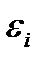или, что то же самое, находится на i -ом энергетическом уровне (в i -ом квантовом состоянии).
При заданных внешних условиях (объем, температура, давление) вероятность состояния частицы, очевидно, должна зависеть только от энергии состояния. Вероятность p одновременно найти частицу 1 в состоянии с энергией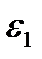 
, а частицу 2 в состоянии с энергией 
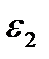, как вероятность двух независимых событий, должна быть равна произведению вероятностей состояний с энергие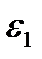й и 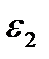, т.е. должно выполняться равенство
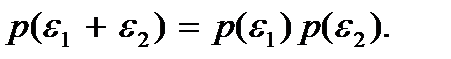
Отсюда следует, что функция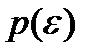 
должна иметь экспоненциальный вид, т.е. p ~ 
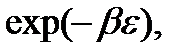так как только экспоненциальный вид зависимости приводит к перемножению функций при сложении аргументов. Из такого вида зависимости p от ε вытекают следствия, которые можно сопоставить с экспериментом. При этом совпадение получается, если принять 
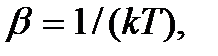где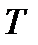 
– температура системы.
Учтем теперь, что каждый энергетический уровень 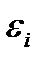в общем случае 
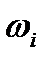-кратно вырожден. Это означает, что имеется 
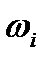возможных состояний частицы с тем же значением энергии 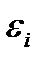(но отличающихся каким-либо другим физическим параметром). Величину 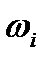называют также статистическим весом состояния (или уровня энергии). Величина 
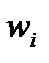определяет максимально возможное число частиц с заданным значением энергии 
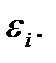Поскольку все эти состояния равноправны, а значит, и равновероятны, то вероятность того, что частица окажется в каком-либо одном из этих состояний, будет просто пропорциональна этому числу состояний 
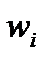: p ~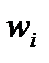 
. Действительно, чем больше состояний с данной энергией 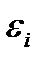, тем с большей вероятностью можно обнаружить частицу в одном из них. Объединяя обе эти зависимости, для искомой вероятности обнаружения частицы в состоянии с энергией 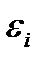будем иметь
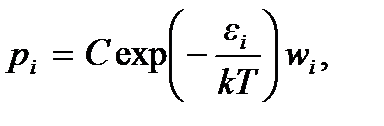
где С – коэффициент пропорциональности. Его можно найти из того условия (условия нормировки), что сумма вероятностей всех состояний частицы должна быть равна единице, так как любая взятая наугад частица достоверно находится в одном из разрешенных состояний. Поэтому
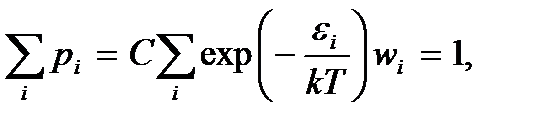
откуда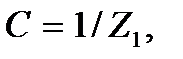 
где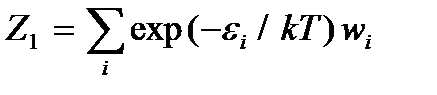 
– так называемая одночастичная сумма по состояниям, или одночастичная статистическая сумма. С учетом этого получим
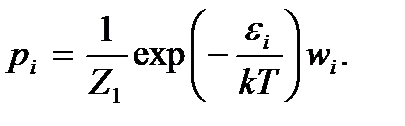(3.5)
Зная вероятность того, что частица находится в состоянии с энергией 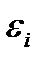, можно определить число 
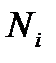частиц, обладающих этой энергией:
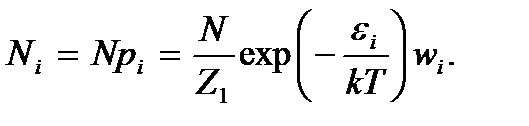(3.6)
Выражение (3.6) носит название распределения Больцмана по энергиям частиц с дискретным спектром. Часто это распределение записывают в виде
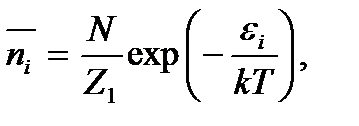(3.7)
где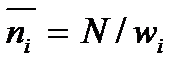 
- среднее число частиц, находящихся в i -ом состоянии. Это выражение можно привести к виду
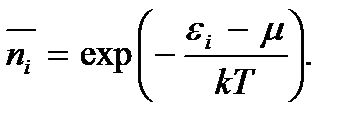(3.8)
Здесь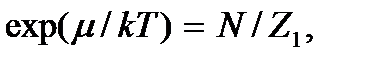 
откуда 
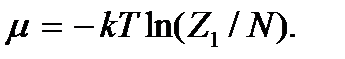Величину μ называют химическим потенциалом системы.
Взяв отношение выражений (3.6) для двух значений энерги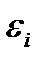и 
и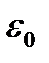 
и принимая, что отношение 
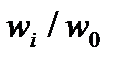не существенно отличается от единицы (при малых i), получим число частиц 
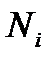на уровне 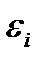по известному числу частиц 
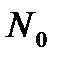на уровне :
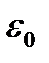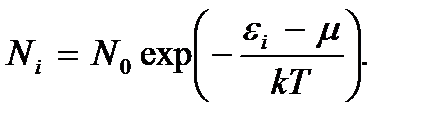
Уровень 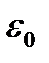можно принять за начало отсчета энергии, т.е. положить 
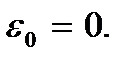Тогда получим
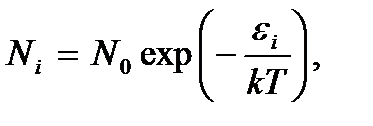(3.9)
где 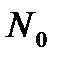– число частиц в основном состоянии.
Зная распределение частиц по энергии, можно определить среднюю энергию частицы. Она находится умножением величины энергии на вероятность обладать этим значением энергии и суммированием всех таких произведений, т.е. как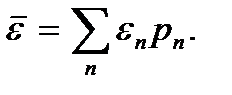 
Подставляя сюда выражение (3.9), получим
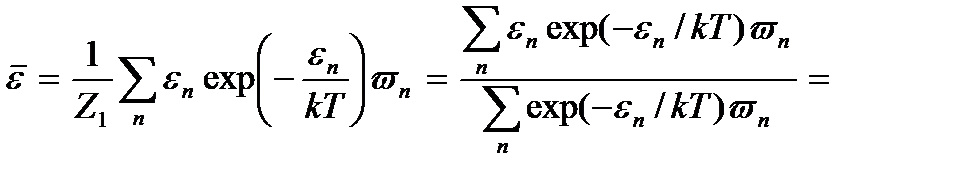
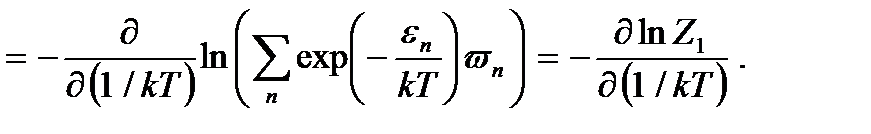(3.10)
