Глава 3
Число состояний микрочастицы
Во всем дальнейшем изложении важную роль будет играть понятие о числе квантовых состояний, соответствующих значениям энергии частицы в некотором заданном интервале. В квантовом случае – это число уровней энергии частицы 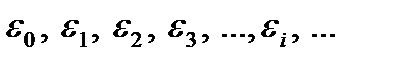 , лежащих в заданном интервале и кратность вырождения каждого уровня
, лежащих в заданном интервале и кратность вырождения каждого уровня 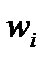 . Так, при движении частицы в одномерной потенциальной яме между точками x = 0 и x = l кратность вырождения каждого уровня
. Так, при движении частицы в одномерной потенциальной яме между точками x = 0 и x = l кратность вырождения каждого уровня 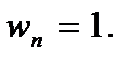 Поэтому в этом случае число состояний равно числу уровней энергии. Если взять значение энергии частицы в интервале от 0 до некоторого значения ε, то число уровней будет равно квантовому числу n при заданном значении
Поэтому в этом случае число состояний равно числу уровней энергии. Если взять значение энергии частицы в интервале от 0 до некоторого значения ε, то число уровней будет равно квантовому числу n при заданном значении 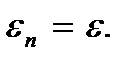 Из формулы энергии частицы в одномерной потенциальной яме
Из формулы энергии частицы в одномерной потенциальной яме 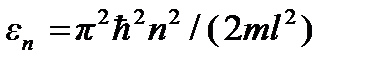 находим
находим 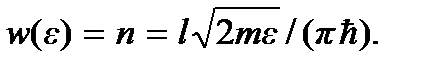 Это и есть число состояний частицы, движущейся в одномерной потенциальной яме с энергией в интервале от 0 до ε. Аналогично можно найти и число состояний микрочастицы с энергией в интервале от 0 до ε, совершающей гармонические колебания (квантового гармонического осциллятора). Так как уровни энергии не вырождены, то число состояний и здесь равно числу уровней энергии в указанном интервале. Учитывая, что расстояния между любыми двумя соседними уровнями квантового гармонического осциллятора одинаковы и равны
Это и есть число состояний частицы, движущейся в одномерной потенциальной яме с энергией в интервале от 0 до ε. Аналогично можно найти и число состояний микрочастицы с энергией в интервале от 0 до ε, совершающей гармонические колебания (квантового гармонического осциллятора). Так как уровни энергии не вырождены, то число состояний и здесь равно числу уровней энергии в указанном интервале. Учитывая, что расстояния между любыми двумя соседними уровнями квантового гармонического осциллятора одинаковы и равны 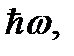 где ω – частота колебаний осциллятора, то указанное число состояний можно найти, разделив ширину указанного интервала энергии на расстояние между уровнями
где ω – частота колебаний осциллятора, то указанное число состояний можно найти, разделив ширину указанного интервала энергии на расстояние между уровнями 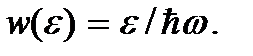
На примере движения микрочастицы в одномерной потенциальной яме мы видели, что дискретность уровней энергии проявляется тем ярче, чем меньше масса m частицы, ширина ямы l и квантовое число n. Наоборот, при больших значениях m, l, n квантование энергии проявляется сравнительно слабо. Эти выводы имеют общий характер. В молекулярно-кинетической теории газов приходится иметь дело со сравнительно тяжелыми частицами (молекулами), движущимися в макроскопических объемах, границы которых представляют собой для частиц газа трехмерную бесконечно глубокую потенциальную яму. Для таких систем квантование энергии играет сравнительно малую роль. Так, в случае поступательного движения молекулы квантованием энергии можно пренебречь, но внутренние движения (вращение и колебание), происходящие в микроскопическом объеме (внутри молекулы), имеют квантовый характер и ими не всегда можно пренебречь. В любом случае квантованием энергии можно пренебречь, если температура термодинамической системы такова, что расстояние между соседними уровнями энергии частицы окажется не больше средней тепловой энергии частицы, т.е. при
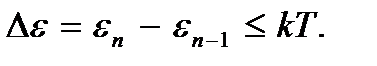 (3.1)
(3.1)
Таким образом, в области высоких температур возможен переход к так называемому квазиклассическому способу описания. Суть его состоит в том, что состояние частицы, как и в классической механике, определяется заданием трех координат x, y, z и трех проекций импульса px, py, pz, но при этом принимается, что, в соответствии с принципом неопределенности, эти величины одновременно могут быть определены лишь с точностью, не превышающей той, которая дается соотношениями неопределенностей
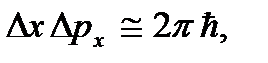
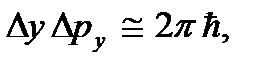
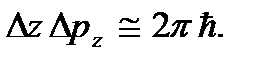 (3.2)
(3.2)
Для определения числа состояний в квазиклассическом приближении введем в рассмотрение так называемое фазовое или μ -пространство. Так называют воображаемое пространство шести измерений, по шести осям которого откладывают три координаты x, y, z и три проекции импульса px, py, pz. Состояние одной частицы по классическим (неквантовым) представлениям в таком пространстве изображается одной точкой (эту точку называют изображающей точкой), а состояние системы N частиц – совокупностью N точек. Такое шестимерное пространство можно рассматривать как совокупность обыкновенного (физического) трехмерного пространства координат и трехмерного пространства импульсов. Учтем теперь, что в соответствии с принципом неопределенности значения координат и импульсов частицы невозможно определить точнее, чем это диктуется соотношениями неопределенностей (3.2). Поэтому два состояния частицы с координатами, например, x и x + ∆ x и проекциями импульсов px и px + ∆ px можно отличить друг от друга лишь в том случае, если эти величины будут не меньше тех, которые допускаются соответствующим соотношением неопределенностей.
Перемножив левые и правые части соотношений (3.2), получим
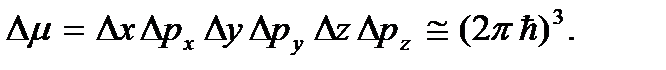
Как видим, величина 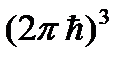 определяет наименьший объем ячейки в фазовом μ -пространстве. Отсюда следует, что в фазовом μ -пространстве каждому состоянию частицы соответствует не одна изображающая точка, а целая фазовая ячейка, объем которой
определяет наименьший объем ячейки в фазовом μ -пространстве. Отсюда следует, что в фазовом μ -пространстве каждому состоянию частицы соответствует не одна изображающая точка, а целая фазовая ячейка, объем которой 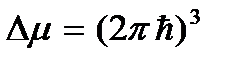 . Это означает также, что на каждое квантовое состояние частицы в фазовом пространстве приходится фазовая ячейка объемом
. Это означает также, что на каждое квантовое состояние частицы в фазовом пространстве приходится фазовая ячейка объемом 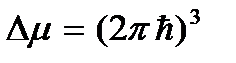 . О частицах, состояниям которых соответствуют определенные фазовые ячейки, говорят, что они находятся в этих ячейках.
. О частицах, состояниям которых соответствуют определенные фазовые ячейки, говорят, что они находятся в этих ячейках.
В квазиклассическом приближении число состояний частицы – это число фазовых ячеек, содержащихся в объеме фазового пространства, соответствующем заданному интервалу энергии. Пользуясь этим приближением, найдем число состояний одной частицы, движущейся в объеме V, с энергией, не превышающей некоторого значения ε. Так как энергия частицы, не находящейся во внешнем силовом поле,
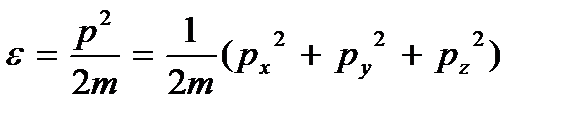 ,
,
то
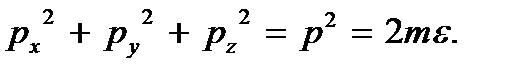
В пространстве импульсов это есть уравнение сферы радиусом  . Следовательно, состояниям частицы с определенным значением энергии ε, а значит, и с определенным значением импульса p в пространстве импульсов соответствует сфера радиусом
. Следовательно, состояниям частицы с определенным значением энергии ε, а значит, и с определенным значением импульса p в пространстве импульсов соответствует сфера радиусом  , а состояниям с энергией, не превышающей ε, и импульсом, не превышающим значения р, – шар, объем которого равен
, а состояниям с энергией, не превышающей ε, и импульсом, не превышающим значения р, – шар, объем которого равен 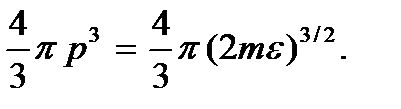 Состояниям с импульсом в интервале от p до p + dp соответствует объем шарового слоя, заключенного между сферами радиуса p и p + dp. Этот объем равен
Состояниям с импульсом в интервале от p до p + dp соответствует объем шарового слоя, заключенного между сферами радиуса p и p + dp. Этот объем равен 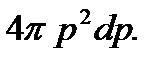 В μ -пространстве этим состояниям соответствует объем
В μ -пространстве этим состояниям соответствует объем 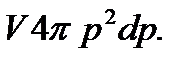 Разделив этот объем на объем, приходящийся на одно состояние
Разделив этот объем на объем, приходящийся на одно состояние 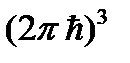 , получим число состояний частицы с импульсом, заключенным в интервале от p до p + dp:
, получим число состояний частицы с импульсом, заключенным в интервале от p до p + dp:
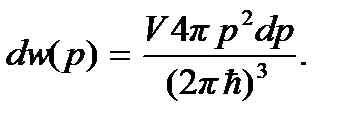 (3.3)
(3.3)
Выразив по формуле  импульс через энергию, получим число состояний частицы, движущейся в объеме V, приходящихся на интервал энергии от ε до ε + dε:
импульс через энергию, получим число состояний частицы, движущейся в объеме V, приходящихся на интервал энергии от ε до ε + dε:
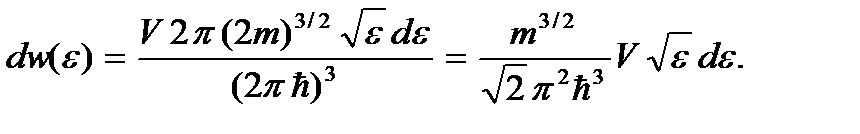 (3.4)
(3.4)
Таким образом,. dw (ε) ~ 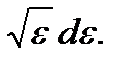
Пользуясь квазиклассическим приближением, получим снова число состояний частицы, движущейся в одномерной потенциальной яме и совершающей гармонические колебания с частотой ω. Фазовое пространство для частицы в потенциальной яме будет плоскостью 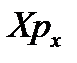 . Фазовая траектория при движении частицы вдоль оси
. Фазовая траектория при движении частицы вдоль оси 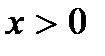 будет представлять собой отрезок
будет представлять собой отрезок 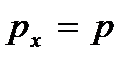 длиной l (рис. 3.1). После отражения от границы ямы
длиной l (рис. 3.1). После отражения от границы ямы 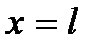 импульс, не меняясь по величине, изменит направление на про-
импульс, не меняясь по величине, изменит направление на про-
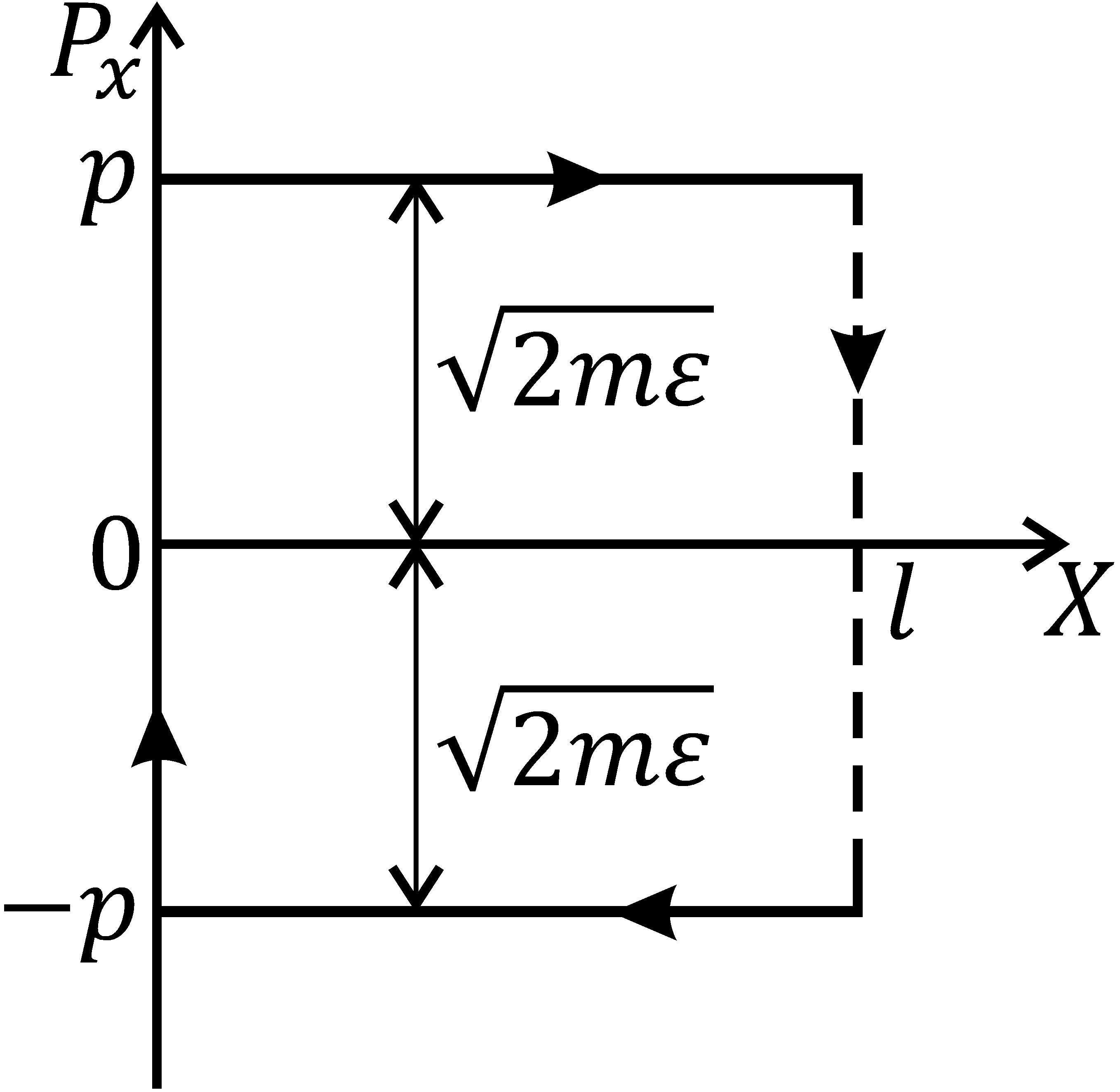 Рис. 3.1 Рис. 3.1 |
тивоположное. Теперь фазовая траектория изобразится отрезком 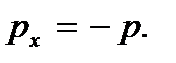 Расстояние между этими отрезками по вертикали будет
Расстояние между этими отрезками по вертикали будет 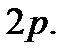 Фазовый объем – площадь прямоугольника, ограниченная указанными отрезками, а также осью px и прямой x = l. Учитывая, что
Фазовый объем – площадь прямоугольника, ограниченная указанными отрезками, а также осью px и прямой x = l. Учитывая, что 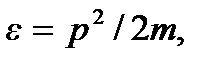 получим
получим
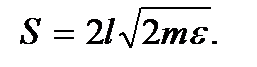
Объем, приходящийся на одно состояние, в одномерном случае равен 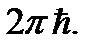 Разделив площадь S на
Разделив площадь S на 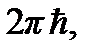 придем к числу состояний, в точности равном ранее полученному значению
придем к числу состояний, в точности равном ранее полученному значению
Фазовая траектория частицы, совершающей гармонические ко-
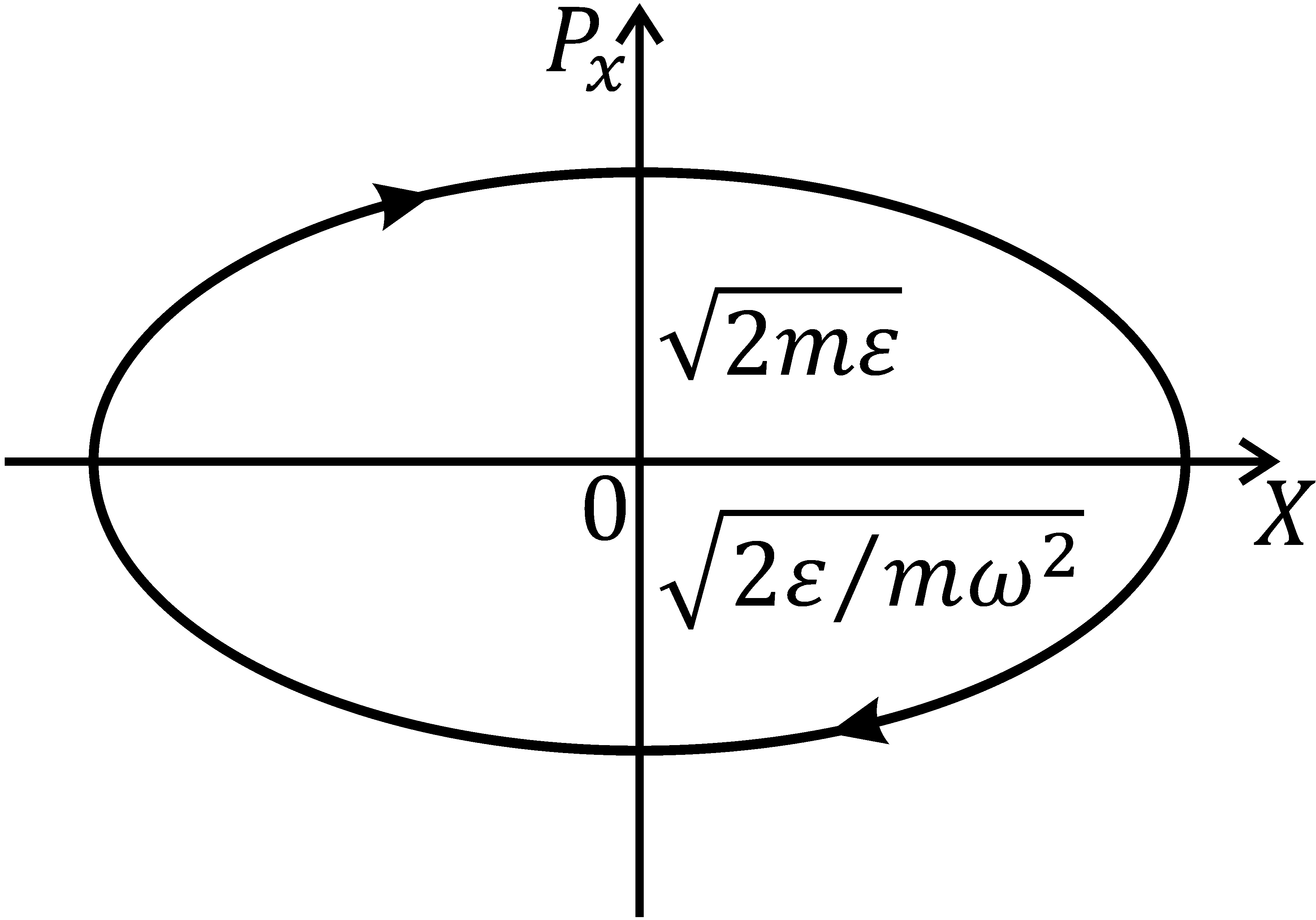 Рис. 3.2 Рис. 3.2 |
лебания, на плоскости 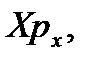 как было показано в разделе «Механические колебания», представляет собой эллипс (рис. 3.2) с полуосями
как было показано в разделе «Механические колебания», представляет собой эллипс (рис. 3.2) с полуосями 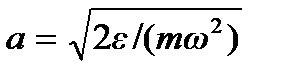 и
и 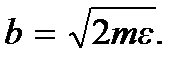 Фазовым объемом будет площадь этого эллипса:
Фазовым объемом будет площадь этого эллипса:
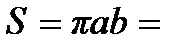
= 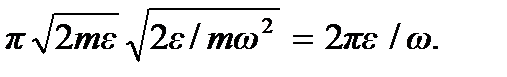
Разделив эту площадь на объем ячейки 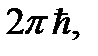 мы снова придем к полученному ранее выражению
мы снова придем к полученному ранее выражению 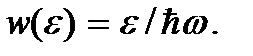
 2015-09-06
2015-09-06 949
949







