Теоретичні відомості

Математичним маятником називають матеріальну точку вагою Р, підвішену на невагому нерозтяжну нитку, яка рухається у вертикальній площині під дією сили тяжіння. Фізичне тіло вважають матеріальною точкою, якщо його розмірами можна знехтувати порівняно з довжиною підвісу.

Рис. 1.1

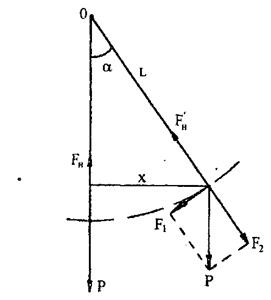У будь-якому положенні математичного маятника на нього діють сила тяжіння Р та сила натягу нитки F_н. У ве­ртикальному положенні маятника ці дві сили врівноважуються, маятник перебуває в стані спокою (положення рівноваги) (рис.1.1). Якщо маятник відхилити на деякий кут α від поло­ження рівноваги, то складова сили тяжіння, спрямована вздовж нитки (нормальна скла­дова, F₂=Р cosα), зрівноважиться силою натягу нитки. Тангенціальна складова F₁ = P sin α, що діє вздовж дуги траєкторії, намагається повернути маятник у положення рівноваги.

Виберемо декартову систему координат так, щоб вісь Y була спрямована вздовж під­вісу вгору, а вісь Х – праворуч. Тоді рівняння руху матеріальної точки згідно з другим законом Ньютона матиме вигляд

ma_t = – P sin α

або

a_t = – g sinα, (1.1)

де а_t – тангенціальне або дотичне прискорення; g – прискорення вільного па­діння. Знак мінус означає, що складова сили F₁ спрямована проти напрямку осі Х. Якщо кут досить малий (не перевищує 6⁰), то sin α ≈ α і рівняння (1.1) матиме вигляд

a_t = – g α. (1.2)

Оскільки кут α = sinα = x / l, де l – довжина математичного маятника, тобто від­стань від точки підвісу до центра тяжіння маятника; х – зміщення від положення рівноваги, то

a_t = 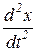= – g 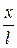. (1.3)

Коливання маятника називають гармонічними, якщо зміщення х від поло­ження рівноваги змінюється за законом

х = х₀ sin ( ω t+ φ ₀), (1.4)

де х₀ – амплітуда коливань; ω t + φ₀ – фаза коливань, яка визначає частку пері­оду, що пройшов від початку коливань до моменту часу t; φ₀ – значення фази в момент часу t = 0 (початкова фаза коливань); ω – кутова, або циклічна, частота, яку обчислюють за співвідношенням

ω = 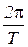, (1.5)

де Т – період коливань.

Звідси, двічі продиференціювавши рівняння (1.4) за часом і порівнявши з виразом (1.4), одержимо

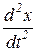= – ω ² x₀ sin ( ω t + φ ₀) = – ω ² x. (1.6)

Порівнюючи співвідношення (1.3) та (1.6), одержимо, що за малих кутів

ω² = .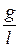

Враховуючи співвідношення (1.5),

Т = 2 π 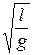. (1.7)

Із формули (1.7) випливає, що період коливання математичного маятника не за­лежить від амплітуди коливань (початкового кута відхилення α₁, якщо α < 6⁰) і маси маятника, а визначений відношенням його довжини до прискорення ві­льного падіння.

Формула (1.7) правдива тільки щодо незгасаючих коливань. Оскі­льки в нашому випадку згасання незначне, вважатимемо, що дана формула слушна й у разі слабозгасаючих коливань.

Таким чином, вимірявши період коливань математичного маятника певної дов­жини, можемо визначити величину прискорення вільного падіння.