Типы симметрии колебаний и характеры представлений

D 6 h

I

2 C 6

2 C 3

C 2

3 C 2'

3 C 2''

i

2 S 3

2 S 6

s h

3s d

3s h

Комплексный вектор 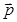дипольного момента и поляризуемости a

A 1 g

a xx +a yy,a zz

A 2 g

–1

–1

–1

–1

B 1 g

–1

–1

–1

–1

–1

B 2 g

–1

–1

–1

–1

–1

–1

E 1 g

–1

–2

–1

–2

a yz,a zx

E 2 g

–1

–1

–1

–1

a xx – a yy, a xy

A 1 u

–1

–1

–1

–1

–1

–1

A 2 u

–1

–1

–1

–1

–1

–1

pz

B 1 u

–1

–1

–1

–1

–1

–1

B 2 u

–1

–1

–1

–1

–1

–1

E 1 u

–1

–2

–2

–1

p x, p y

E 2 u

–1

–1

–2

–2

В группах более высокой симметрии встречаются колебания дважды (Е) и трижды (F) вырожденные. Вырождение связано с тем, что нельзя выделить колебательные координаты, соответствующие отдельным степеням свободы, которые при операциях симметрии преобразовывались бы независимо друг от друга. При этом кратность вырождения равна числу существенным образом связанных друг с другом координат. Колебания называют вырожденными, если различным формам движения атомов в молекуле соответствует одна частота.

Первоочередной задачей теоретико-группового анализа колебаний является определение для заданной группы общего числа различных типов симметрии каждой степени вырождения. для любой группы оно равно числу m классов симметрии. Для абелевых групп число классов m равно порядку группы, откуда следует, что для низшей симметрии число типов симметрии равно порядку группы h. Для неабелевых групп число классов меньше порядка группы, поэтому число типов симметрии всегда меньше порядка группы.

Существует общая формула, позволяющая определить для заданной точечной группы число типов симметрии с различной степенью вырождения. Пусть степень вырождения i -го типа равна l_i (i = 1,2, 3,... m, где m – число классов). Тогда порядок группы h равен

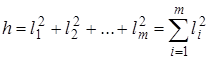, (4.83)

т. е. порядок группы равен сумме квадратов степеней вырождения всех возможных типов симметрии. При этом разложение (4.83) порядка группы на сумму m квадратов является единственным. Для абелевых групп все I_i равны единице и h равно сумме h единиц.

Для молекулы воды порядок группы равен 4 и соответственно сумма квадратов кратностей вырождения 1²+ 1² + 1² + 1² = 4 (здесь все колебания невырожденные). Для молекулы бензола C₆H₆ имеем h = 24 (см. табл. 4.8), a m = 12 и сумма квадратов кратностей вырождения:

h = l² + l² + 1 ²+ 1² + 2² + 2² + 1² + l² +1² + 1² + 2² +2² = 24.

Причем разложение порядка группы на сумму квадратов степеней вырождения всегда однозначно.

Важнейшей характеристикой преобразований координат при операциях симметрии являются характеры матриц χ – суммы диагональных элементов матриц преобразования. Характеры не зависят от выбора исходных координат, одинаковых для операций симметрии, принадлежащих к одному классу. Поэтому обычно указывают характер сразу для всех операций, относящихся к данному классу. Для всех точечных групп симметрии составлены таблицы характеров, которыми необходимо уметь пользоваться в колебательной и электронной спектроскопии.