2015-09-06
759
точечной группы симметрии D6 h
| Операция симметрии | I | 2 C 6 | 2 C 3 | C 2 | 3 C 2 ' | 3 C 2¢¢ |
| Вид вращения | правильное | |||||
| φ | 0° | 60° | 120° | 180° | 180° | 180° |
| 1 + 2cos φ | –1 | –1 | –1 | |||
| N(R) | ||||||
| c= ±NR (1 + 2cos φ) | –4 | |||||
| ct= ±(1 +2cos φ) | –1 | –1 | –1 | |||
| cr= (1 + 2cos φ) | –1 | –1 | –1 | |||
| cu=c – ct – cr | –4 | –2 | ||||
| Операция симметрии | i | 2S3 | 2S6 | s h | 3s d | 3su |
| Вид вращения | неправильное | |||||
| φ | 0° | 60° | 120° | 180° | 180° | 180° |
| 1 + 2cos φ | –1 | –1 | –1 | |||
| N(R) | ||||||
| c = ±N R (1 + 2cos φ) | ||||||
| c t = ±(1 + 2cos φ) | –3 | –2 | ||||
| c r = (1 + 2cos φ) | –1 | –1 | –1 | |||
| cu = c – c t – c r |
Применяя формулу (4.84), получим:
......................................................................
... 
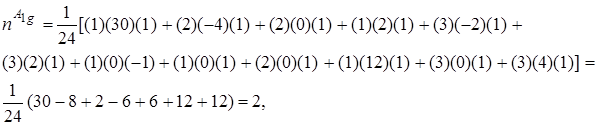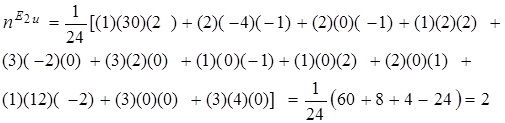
В результате все тридцать колебаний молекулы бензола распределяются между следующими типами симметрии:
Гv = 2 A 1 g + A 2 g + 2 B 2 g + E 1 g + 4 E 2 g + A 2 u + 2 B 1 u + 2 B 2 u + 3 E 1 u + 2E2 u.
знание только симметрии молекулы позволяет сравнительно простым расчетом определить число колебаний того или иного типа симметрии.
|
|
|
Аналогичное распределение колебаний по типам симметрии можно получить, решив колебательную задачу для молекулы на ЭВМ, однако это потребовало бы намного больших усилий и затрат времени. Для сравнения расчетных значений частот колебаний молекулы бензола с экспериментальными (см. табл. 4.11).
Таблица 4.11
