Упражнение 11. Упражнение 15*. (теорема о средней линии треугольника)

а)Докажите, что геометрическим местом точек плоскости (ГМТ), равноудалённых от двух пересекающихся прямых, является пара прямых -биссектрис образованных ими вертикальных 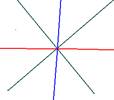углов. б) докажите, что эти две биссектрисы всегда взаимно перпендикулярны.

Упражнение 12. *

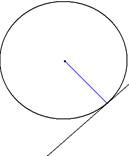
Докажите, что прямая, перпендикулярная радиусу и инцидентная его концу, является касательной к окружности. Обратно, касательная к окружности перпендикулярна радиусу, проведённому к точке касания.

Упражнение 13.

Докажите, что у любого треугольника существует, и при том единственная, вписанная в него окружность.

Упражнение 14.

a) Докажите, что если диагонали некоторого четырехугольника делятся их точкой пересечения пополам, то этот четырехугольник – параллелограмм;

b) Докажите, что если у некоторого четырехугольника имеется пара сторон, которые конгруэнтны и параллельны, то этот четырехугольник – параллелограмм.

Def.

Отрезок, соединяющий середины сторон треугольника, называется его средней линией.

Упражнение 15*. (теорема о средней линии треугольника)

a) 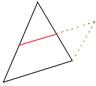Средняя линия треугольника параллельна его третьей стороне и вдвое меньше её.

b) если в треугольнике отрезок, соединяющий две его стороны, параллелен третьей его стороне и вдвое меньше её, то он – средняя линия в этом треугольнике.

c) если прямая делит одну сторону треугольника пополам и параллельна второй его стороне, то третью сторону треугольника она тоже делит пополам.

Упражнение 16. (Теорема Вариньона)

Пусть АВСD – произвольный четырехугольник, возможно даже невыпуклый. Пусть M, N, K и L – середины сторон АВ, ВС, CD и DE соответственно. Тогда четырехугольник MNKL - параллелограмм.

Упражнение 17.

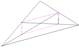Медианы в треугольнике делятся точкой их пересечения в отношении 2:1, считая от вершин. В частности, все три медианы пересекаются в одной точке.