Ми вже розглядали закони функціонування, математичні моделі комбінаційних схем.
Розглянемо закон функціонування цифрових автоматів з погляду абстрактної теорії автоматів.
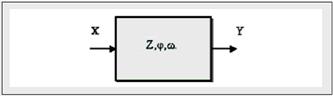
Рисунок 4.1 – Модель абстрактного цифрового автомата
Абстрактний автомат А − це узагальнене представлення опису функціонування моделі цифрової логічної системи у дискретному часі, яку визначають:
- множиною вхідних сигналів 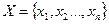 ;
;
- множиною вихідних сигналів 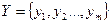 ;
;
- множиною внутрішніх станів 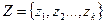 , включаючи й початковий, нульовий стан z0;
, включаючи й початковий, нульовий стан z0;
- функцією переходів 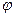 відображення множини вхідних сигналів
відображення множини вхідних сигналів 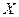 на множину внутрішніх станів
на множину внутрішніх станів 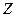 ;
;
- функцією виходів відображення множини вхідних сигналів 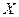 і станів
і станів 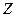 на множину вихідних сигналів
на множину вихідних сигналів 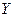 .
.
Тоді, узагальнений закон або модель абстрактного автомата буде виглядати як математичний кортеж:
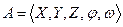 .
.
Автомат називають кінцевим, якщо кінцеві множини 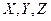 . Абстрактний автомат реалізує відображення множини слів вхідного алфавіту X на множину слів вихідного алфавіту Y.
. Абстрактний автомат реалізує відображення множини слів вхідного алфавіту X на множину слів вихідного алфавіту Y.
Узагальнений закон функціонування автомата не відтворює його поведінку в часі, а саме це питання є іноді основним при аналізі й синтезі цифрових систем. Серед багатьох спроб дати математичний опис поведінки автомата в часі, найбільше поширення одержали автомати Мілі й Мура.
Закон функціонування автомата Мілі:
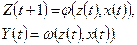
Наступний стан автомата 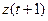 залежить від функції переходів φ, стану автомата на даний час z(t) і вхідних сигналів у цей момент часу
залежить від функції переходів φ, стану автомата на даний час z(t) і вхідних сигналів у цей момент часу 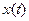 . Вихідні сигнали залежать від функції виходів w, вхідних сигналів x(t) і внутрішнього стану автомата
. Вихідні сигнали залежать від функції виходів w, вхідних сигналів x(t) і внутрішнього стану автомата 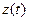 , де
, де 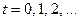 − автоматний, дискретний час визначений тактовими імпульсами; z 0 − початковий, нульовий стан.
− автоматний, дискретний час визначений тактовими імпульсами; z 0 − початковий, нульовий стан.
Закон функціонування автомата Мура:
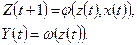
Тобто, в автоматі Мура вихідні сигнали 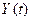 залежать тільки від стану автомата в цей момент і не залежать від вхідних сигналів.
залежать тільки від стану автомата в цей момент і не залежать від вхідних сигналів.
 2015-09-06
2015-09-06 291
291








