Модель межвидовой конкуренции Лотки-Вольтерры (Lotka-Volterra Competition)

Модели зависимого от плотности роста, такие как логистическое ура­внение, описывают процесс внутривидовой конкуренции, при котором по мере увеличения численности особей ресурсы становятся все более огра­ничивающим фактором, и удельная скорость роста популяции умень­шается. Модель межвидовой конкуренции Лотки-Вольтерры (Lotka, 1925; Volterra, 1926) построена на основе логистического уравнения и по существу несет в себе все его недостатки. Однако, несмотря на это, данная модель является наиболее простым и с исторической точки зре­ния очень важным способом анализа межвидовой конкуренции. Она может помочь выявить основные факторы, определяющие исход конкурентного взаимодействия двух видов.

Пусть N₁ -численность популяции первого вида, N₂-численность вто­рого, а предельные плотности насыщения и максимальные удельные скорости роста этих популяций составляют, соответственно, K₁, К₂, r₁ и r₂. Предположим далее, что 10 особей вида 2 при конкуренции все вместе оказывают такое же ингибирующее влияние на вид 1, как одна особь вида 1. Это фактически означает, что каждая особь вида 2 использует лишь 1/10 емкости среды K₁, занимаемой каждой особью вида 1. Тогда совместное воздействие внутри- и межвидовой конкуренции на вид 1 будет равноценно воздействию (N₁+ N₂/10) особей вида 1. Константа 1/10 в данном выражении называется коэффициентом конкуренции и обозначается через α (или через α₁₂ - "альфа один - два"). С помощью этого коэффициента, величина которого зависит, прежде всего, от степени сходства потребностей видов в тех или иных ресурсах, оценивают конкурентное воздействие вида 2 на вид 1 в расчете на одну особь. Умножая N₂ на α, мы выражаем это воздействие через эквивалентное число особей N₁. Обратите внимание, что α < 1 означает, что вид 2 оказывает меньшее подавляющее влияние на вид 1, чем вид 1 на самого себя, а α > 1 означает, что ингибирующее воздействие со стороны вида 2 на вид 1 выражено в большей степени, чем со стороны особей своего вида. Аналогичным образом конкурентное воздействие вида 1 на вид 2 выражают коэффициентом β (или по другой терминологии α ₂₁ - "альфа два-один").

Важнейшим преобразованием логистического уравнения в модели Лотки-Вольтерры является замена N₁ в скобках на выражение " N₁ плюс число эквивалентов N₁^”, т.е. на (N₁+ α N₂). Тогда логистическое уравнение роста для первого вида можно записать следующим образом:

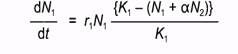
или: 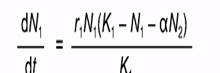(1)

и для второго вида:

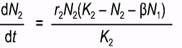(2)

Из двух уравнений 1 и 2 и состоит модель Лотки-Вольтерры.

При исследовании свойств этой модели, мы должны, прежде всего, ответить на вопрос: при каких условиях увеличивается или уменьшается численность каждого вида? Для этого нужно построить диаграммы, на которых могут быть изображены все возможные сочетания численностей вида 1 и вида 2, т.е. значений N₁ и N₂. На таких графиках, обычно называемых фазово-плоскостными диаграммами, или фазовыми портретами, значения N, отложены по оси абсцисс, а N₂ - по оси ординат, так что численность обоих видов снижается вниз и влево, а возрастает вверх и вправо. Одни сочетания N₁ и N₂ будут вызывать увеличение численности вида 1 и (или) вида 2, тогда как другие будут приводить к уменьшению численности вида 1 и (или) вида 2. Кроме того, для каждого вида можно провести изоклину, т.е. линию, соединяющую точки, в которых скорость роста популяции данного вида равна нулю. Изоклина отделяет на диаграмме те сочетания N₁ и N₂, при которых наблюдается рост популяции данного вида, от тех сочетаний, при которых популяция вида сокращается.

Для того, чтобы провести изоклину для вида 1, воспользуемся тем, что на этой линии по определению dN/dt=0. Поэтому из уравнения 1 следует:

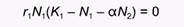
Это выражение справедливо в трех случаях: (1) когда удельная скорость роста популяции r₁ равна нулю, (2) когда численность популяции (N₁ равна нулю и (3) когда

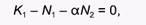
что можно записать как

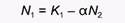(3)

Другими словами, в любой точке прямой линии, которую описывает это уравнение, dN/dt = 0. Следовательно, эта линия и является изоклиной для вида 1, а поскольку она представляет собой прямую, то ее можно провести, определив всего две точки и затем соединив их. Так, из уравнения 2 следует, что:

при 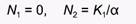(точка на оси ординат)

при (точка на оси абсцисс)

Соединив эти две точки, получим изоклину для вида 1. Точно таким же образом определим условия, которые приводят к увеличению или уменьшению вида 2 и проведем изоклину для него:

при 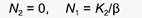(точка на оси абсцисс)

при 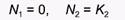(точка на оси ординат)

Для того, чтобы в этой модели определить исход конкуренции, необходимо изоклины для двух видов провести на одной диаграмме, что даст возможность предсказывать поведение обеих популяций.