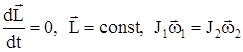
В системе тел момент импульса системы относительно оси вращения будет оставаться постоянным, если момент внешних сил, действующих на систему, относительно оси вращения будет равен нулю.
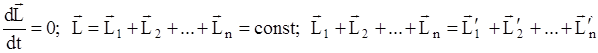
2.8. Некоторые силы в механике
| mg | - сила тяжести, g - ускорение свободного падения. |
| N | - реакция опоры, направленная перпендикулярно плоскости соприкосновения взаимодействующих тел. |
| Fтр = kN | - сила трения, направлена противоположно скорости движения или силе, стремящейся сдвинуть тело, k - коэффициент трения. |
| F = - kx | - сила упругости, k - коэффициент жесткости пружины, х – деформация пружины. |
| Fн | - сила натяжения нити или подвеса, численно равная весу тела. |
| P P = mg P =m(g+а) P = m(g-а) | - вес тела, сила с которой тело действует на опору или подвес. - опора покоится. - опора движется вверх с ускорением а. - опора движется вниз с ускорением а. |
3. Работа и механическая энергия
3.1. Работа силы и мощность при поступательном и вращательном движениях
У материальной точки (тела) в процессе силового взаимодействия с другими телами может изменяться состояние движения (координаты и скорость). В этом случае говорят, что над телом совершается работа. В механике принято говорить, что работа совершается силой.
Элементарной работой силы 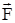 на малом перемещении
на малом перемещении 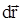 называется величина, равная скалярному произведению силы на перемещение:
называется величина, равная скалярному произведению силы на перемещение:
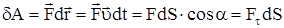 ,
,
где 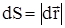 - элементарный путь точки приложения силы за время dt, a- угол между векторами
- элементарный путь точки приложения силы за время dt, a- угол между векторами 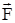 и
и 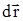 ,
, 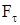 =F×cosa - тангенциальная составляющая силы, равная проекции силы на направление перемещения
=F×cosa - тангенциальная составляющая силы, равная проекции силы на направление перемещения 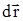 .
.
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности.
Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
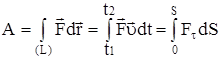 .
.
Если 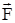 = const, то А=
= const, то А= 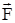
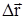 , если
, если 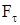 = const, то А=
= const, то А= 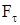 S.
S.
При вращательном движении считается, что работа определяется моментом сил:
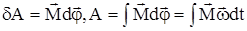 ,
,
если М = const, то А=Мj.
Для характеристики быстроты совершения работы вводится мощность.
Мощностью называется скалярная величина N равная работе, совершаемой в единицу времени.
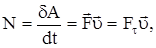
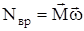 .
.
3.2. Кинетическая энергия при поступательном и вращательном движениях
Кинетической энергией тела называется функция механического состояния тела, зависящая от массы тела и скорости его движения (энергия механического движения).
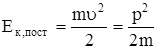 ;
; 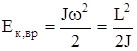 .
.
При сложном движении твёрдого тела, его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:
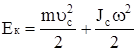
где uc - скорость поступательного движения тела (центра масс), Jc - момент инерции тела относительно мгновенной оси вращения, проходящей через центр масс, w - угловая скорость вращения тела.
Отметим свойства кинетической энергии.
Кинетическая энергия не отрицательна: ЕК³ 0.
Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему: 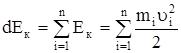 .
.
Приращение кинетической энергии тела или системы равно работе всех сил, действующих на систему или на тело: 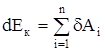 .
.
3.3. Консервативные (потенциальные) силы
Консервативными (потенциальными) силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил - работа на замкнутой траектории тождественно равна нулю:
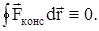
К консервативным силам относятся: сила тяжести, сила упругости и силы, определяющие фундаментальные взаимодействия.
Потенциальная энергия системы - это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил, убыль которой равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.
ЕП1-ЕП2 = -DЕП = А12конс, 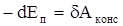 .
.
Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.
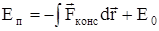 .
.
Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.
Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:
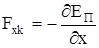 ,
, 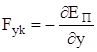 ,
, 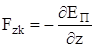 .
.
Примеры потенциальной энергии:
1) 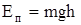 - потенциальная энергия тела массой m, поднятого на высоту h от нулевого уровня энергии в поле тяжести Земли;
- потенциальная энергия тела массой m, поднятого на высоту h от нулевого уровня энергии в поле тяжести Земли;
2) 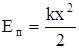 - потенциальная энергия упругого деформированного тела, х - величина деформации тела (пружины).
- потенциальная энергия упругого деформированного тела, х - величина деформации тела (пружины).
3.5. Закон сохранения механической энергии
Полная механическая энергия системы материальных точек равна сумме их кинетической и потенциальной энергии взаимодействия этих точек друг с другом и с внешними телами:
Е = Ек + Еп.
Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):
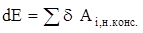 ,
, 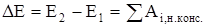
Если действуют только консервативные силы или работа неконсервативных сил равна нулю, то dE = 0 и Е = const, т.е. справедлив закон сохранения механической энергии: при движении консервативной системы её механическая энергия не изменяется.
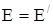 , ЕК+ЕП=ЕК’+ЕП’
, ЕК+ЕП=ЕК’+ЕП’
4. Элементы специальной теории относительности
4.1. Постулаты Эйнштейна. Преобразования Лоренца
| 1. Принцип относительности Никакими физическими опытами, производимыми внутри инерциальной системы отсчета, невозможно установить, покоится ли эта система относительно другой инерциальной системы отсчета или движется прямолинейно и равномерно. 2. Принцип постоянства скорости света Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света. |
Рассмотрим две системы отсчета S и S’ (рис. 8). Систему S будем считать условно неподвижной. Система 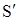 движется относительно
движется относительно 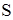 со скоростью
со скоростью 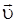 вдоль оси X системы
вдоль оси X системы 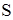 . Для перехода от одной системы отсчета в другую в специальной теории относительности используются преобразования Лоренца. Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают.
. Для перехода от одной системы отсчета в другую в специальной теории относительности используются преобразования Лоренца. Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают.
Рис.8 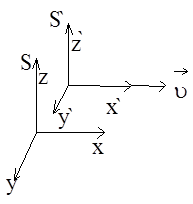
Тогда: 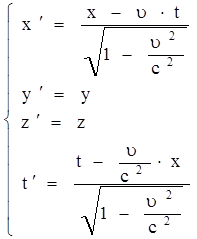
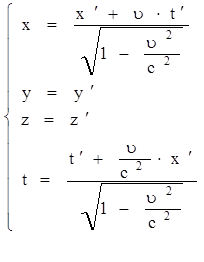
Здесь 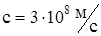 - скорость света в вакууме.
- скорость света в вакууме.
4.2. Следствия из преобразований Лоренца
Будем рассматривать системы 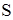 и
и 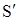 (рис. 8).
(рис. 8).
1. Относительность промежутков времени между событиями.
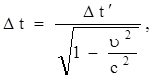
где 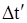 - промежуток времени между событиями, происшедшими в системе отсчета
- промежуток времени между событиями, происшедшими в системе отсчета 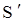 (
(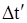 отсчитывается по часам, находящимся в системе
отсчитывается по часам, находящимся в системе 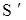 );
);
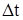 - промежуток времени между этими событиям, отсчитанный по часам, находящимся в системе
- промежуток времени между этими событиям, отсчитанный по часам, находящимся в системе 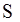 .
.
2. Изменение размеров движущихся тел.
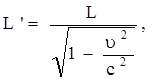
где L’-длина стержня, расположенного вдоль оси 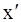 и покоящегося в системе S’ (отсчитывается в системе отсчета S’);
и покоящегося в системе S’ (отсчитывается в системе отсчета S’);
L - длина этого же стержня, измеренная в системе отсчета 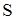 .
.
3. Релятивистский закон сложения скоростей.
Пусть некоторое тело движется вдоль оси x` в системе отсчета 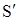 со скоростью
со скоростью 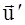 относительно последней. Найдем проекцию скорости
относительно последней. Найдем проекцию скорости 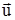 этого тела в системе отсчета
этого тела в системе отсчета 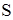 на ось x этой системы:
на ось x этой системы:
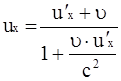 .
.
4.3. Релятивистские масса и импульс. Взаимосвязь массы и энергии
Эйнштейн показал, что масса тела зависит от его скорости:
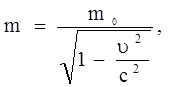
где m0 – масса тела в той системе отсчета, где тело покоится (масса покоя);
m – масса тела в той системе, относительно которой тело движется;
u – скорость тела относительно системы отсчета, в которой определяется масса m.
Релятивистский импульс:
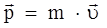 ,
,
где m – релятивистская масса.
Закон взаимодействия массы и энергии:
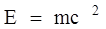 ,
,
где m - релятивистская масса;
E – полная энергия материального объекта.
Кинетическая энергия объекта:
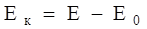 ,
,
где 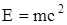 - полная энергия;
- полная энергия;
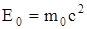 - энергия покоя.
- энергия покоя.
Из закона взаимосвязи массы и энергии следует, что всякое изменение массы тела на Dm сопровождается изменением его энергии на DE:
DE=Dm×c2.
Примеры решения задач
Задача 1 Уравнение движения точки по прямой имеет вид:
x = A+Bt+Ct3, где А = 4 м, В = 2 м/c, С = 0,2 м/с3. Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
Дано:
| x = A + Bt + Ct3 A = 4 м B = 2 м/c C = 0,2 м/c3 t1 = 2 c; t2 = 5 c x1, x2 <u>-? u1, u2 -? <a> a1, a2 -? | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×23) м = 9,6 м, x2 = (4+2×5+0,2×53) м = 39 м. 2. Средняя скорость 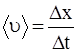 , , 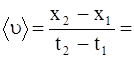 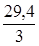 м/с = 9,8 м/с. 3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения: м/с = 9,8 м/с. 3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения: 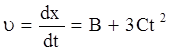 u1=(2+3×0,2×22) м/с = 4,4 м/c; u2=(2+3×0,2×52) м/с = 17 м/с. u1=(2+3×0,2×22) м/с = 4,4 м/c; u2=(2+3×0,2×52) м/с = 17 м/с. |
4. Среднее ускорение 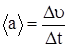 ,
,
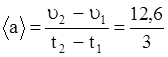 м/c2=4,2 м/с2.
м/c2=4,2 м/с2.
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1=6×0,2×2 м/c2=2,4 м/с2;
a2=6×0,2×5 м/с2=6 м/с2.
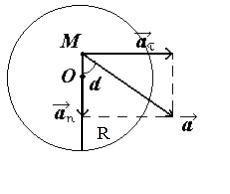
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 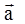 любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
Дано:
| w0 = 0. N = 2 e = const | Решение Разложив вектор 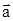 точки М на тангенциальное точки М на тангенциальное 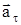 и нормальное и нормальное 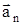 ускорения, видим, что искомый угол определяется соотношением tga=at/an. Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: ускорения, видим, что искомый угол определяется соотношением tga=at/an. Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: |
| a -? |
at = eR, an = w2R, где R – радиус маховика,
 |
получим
tga= 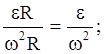
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
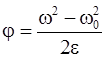 ;
;
Поскольку w0=0; j=2pN, то w2=2e×2pN=4pNe.
Подставим это значение в формулу, получим:
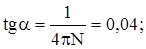 a» 2,3 °.
a» 2,3 °.
Ответ: a» 2,3 °.
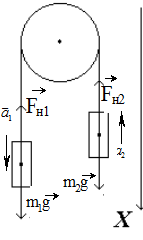
Задача 3 Две гири с массами m1 =2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 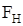 . Трением в блоке пренебречь.
. Трением в блоке пренебречь.
Дано:
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики 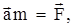 где где 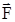 – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело. |
| a, FН -? |
На тело1 и тело 2 действуют только две силы – сила тяжести 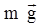 и
и
сила натяжения нити 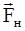 . Для первого тела имеем:
. Для первого тела имеем:
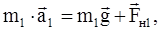 (1)
(1)
 |
для второго тела:
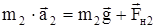 . (2)
. (2)
Так как сила трения в блоке отсутствует,
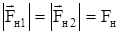 .
.
Ускорения тел а1 и а2 равны по модулю и направлены в противоположные стороны
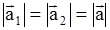 .
.
Получаем из (1) и (2) систему уравнений.
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений 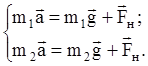
в проекциях на ось Х: 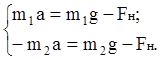
Решая эту систему относительно а и FН, получаем:
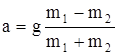 =3,3 м/с2;
=3,3 м/с2; 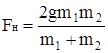 =13 Н.
=13 Н.
Ответ: a= 3,3 м/c2; FH = 13,3 Н
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с2.
Дано:
| R = 0,2 м F = 98,1 Н MТР = 4,3 Н×м e = 100 рад / c2 | Решение Воспользуемся основным законом динамики вращательного движения: 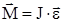 или в скалярной форме или в скалярной форме 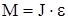 , где , где 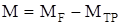 - момент сил, приложенных к телу (MF - момент силы F, Mтр – момент сил трения); - момент сил, приложенных к телу (MF - момент силы F, Mтр – момент сил трения); |
| m -? |
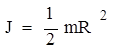 - момент инерции диска.
- момент инерции диска.
Учитывая, что MF=F×R, получаем: 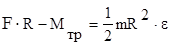 .
.
Отсюда 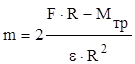
m=3,68 кг.
Ответ: m = 3, 68 кг
 2015-09-06
2015-09-06 1957
1957
