2015-09-06
1309
Каким образом относительно просто описать плазму-систему с громадным! количеством взаимодействующих частиц?
Оказывается, это можно сделать, если плазма находится в так называемом состоянии полного термодинамического равновесия (ПТР). Если плазма находится в ПТР (что выполняется в любой полости с постоянной температурой стенок), то ее физическое состояние можно полностью определить с помощью конечного числа термодинамических переменных. Этими переменными являются температура, давление газа и концентрации элементов.
Для плазмы, находящейся в ПТР, выполняются следующие соотношения.
I) Максвелловское распределение частиц по скоростям.
В состав реальной плазмы кроме электронов и положительно заряженных ионов входят отрицательно заряженные ионы, нейтральные атомы и молекулы. Частицы каждого типа сталкиваются между собой и с частицами других типов, обмениваясь при этом энергией. В результате этого в плазме устанавливается максвелловское распределение частиц каждого типа по скоростям.
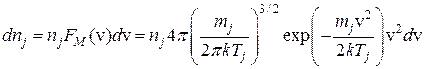, (1)
где 
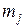и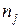 
- масса и концентрация частиц данного типа, 
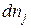- концентрация частиц, имеющих скорости в диапазоне от 
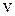до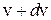 
. Температура 
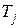характеризует среднюю кинетическую энергию частиц данного типа 
.
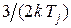II) Больцмановское распределение атомов и ионов по энергетическим уровням.
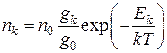, (2)
где 
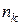и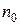 
-концентрации атомов, на 
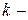ом и основном энергетическом уровнях, соответственно, 
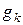и 
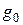-статистические веса этих уровней, 
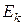-энергия 
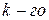уровня (
).
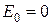III) Ионизационное равновесие (формула Саха).
Эта формула устанавливает соотношение между концентрациями частиц двух последовательных ступеней ионизации. Если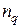 
-концентрация ионов с зарядовым числом 
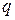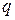( =0 соответствует нейтральному атому), 
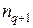-концентрация ионов с зарядовым числом 
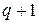, то справедливо соотношение:
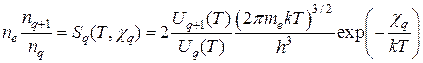, (3)
где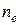 
-концентрация электронов, 
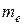-масса покоя электрона, 
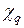-энергия ионизации 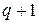-го электрона. Функци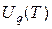и 
и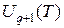 
-статистические суммы, соответствующие двум ступеням ионизации. Статистическая сумма определяется как:
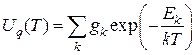. (4)
Отметим, что все температуры в этих соотношениях имеют одно и то же значение: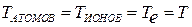 
.
IV) Электромагнитное поле излучения плазмы в состоянии ПТР описывается функцией Планка.
.
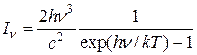Как видно, формула довольно простая: интенсивность зависит только от одного параметра-температуры.
