Технологический прогресс в модели Солоу

Учет в модели Солоу технологического прогресса видоизменяет исходную производственную функцию. Предполагается трудосберегающая форма технологического прогресса. Производственная функция будет представлена как Y=F(K,LA), где A- эффективность труда, а LA - численность условных единиц труда с постоянной эффективностью A. Чем выше A, тем больше продукции может быть произведено данным числом работников.

Пусть 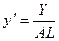, 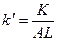(количество капитала в расчете на единицу труда с постоянной эффективностью).

Тогда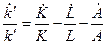

Предлагается, что технологический прогресс осуществляется путем роста эффективности труда A с постоянным темпом g (.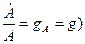

После преобразований получим:

δ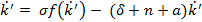

Включение технологического прогресса несколько меняет и анализ состояния устойчивого равновесия, хотя ход рассуждений сохраняется.

В устойчивое состояние система придёт в случае, когда

=

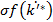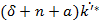
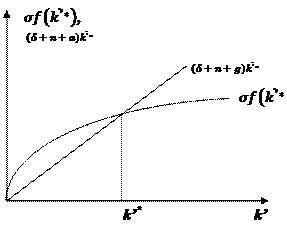В устойчивом состоянии (k′*) при наличии технологического прогресса общий объём капитала (К) и выпуска (Y), будут расти с темпом (n+a). Но в отличие от случая роста населения, теперь будут расти с темпом g фондовооруженность (K/L) и выпуск (Y/L) в расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения (у).

Рис. 6

С учетом роста населения и технологического прогресса «золотое правило» будет иметь следующий вид:

МРК= 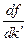= 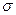+n+a.

Таким образом, в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости