Правило сложения дисперсий

В статистическом исследовании очень часто бывает необходимо не только изучить вариации признака по всей совокупности, но и проследить количественные изменения признака по однородным группам совокупности, а также между группами. Это связано с тем, что общая дисперсия характеризует вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности. Если же необходимо выделить в составе общей дисперсии ту ее часть, которая обусловлена влиянием какого-либо определенного фактора, то следует разбить изучаемую совокупность на группы, положив в основу группировки интересующий нас фактор. Затем нужно изучить раздельно вариацию признака внутри однородных по отношению к данному фактору групп и изменение величины признака от группы к группе. Выполнение такой группировки позволит разложить общую дисперсию признака на две дисперсии, одна из которых будет характеризовать часть вариации, обусловленную влиянием фактора, положенного в основу группировки, а вторая - вариацию, происходящую под влиянием остальных факторов. Следовательно, помимо общей средней для всей совокупности необходимо просчитывать и частные средние величины по отдельным группам. В связи с этим различают три вида дисперсий:

- общую;

- межгрупповую;

- среднюю внутригрупповую.

Общая дисперсия (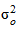) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле

,

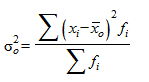где 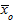- общая средняя арифметическая всей исследуемой совокупности.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия 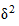(дисперсия групповых средних), которая является мерой разброса частных средних по группам 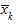вокруг общей средней 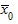и вычисляется по формуле

,

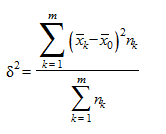где m - число групп, 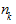- число единиц совокупности в k-й группе, 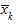- частная средняя величина по k-й группе, 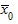- общая средняя величина всей исследуемой совокупности.

Средняя внутригрупповая дисперсия (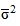) свидетельствует о случайной вариации, которая может возникнуть под влиянием остальных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам ():

,

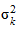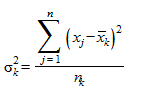а затем рассчитывается средняя внутригрупповая дисперсия ():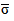

,

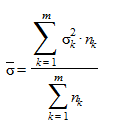где 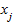- единицы совокупности, входящие в k-ю группу.

Все три вида дисперсии связаны между собой соотношением, определяемым правилом сложения дисперсий: общая дисперсия равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

.

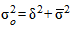Согласно этому правилу общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.

Соотношение межгрупповой и общей дисперсии называется коэффициентом детерминации 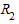, который показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:

.

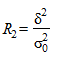Замечание. Для определения степени связи между признаками используют корреляционное отношение (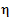), введенное К. Пирсоном. Оно тесно связано с коэффициентом детерминации:

.

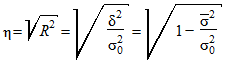Корреляционное отношение изменяется от 0 до 1. Величина корреляционного отношения будет равна 0, когда нет влияния исследуемого фактора на вариацию признака, т.е. вариация обусловлена влиянием других неучтенных факторов. В тех случаях, когда внутригрупповая дисперсия близка к 0, т.е. практически вся вариация признака обусловлена действием исследуемого фактора, величина корреляционного отношения близка к 1.

Пример. По результатам статистического исследования о влиянии уровня образования на уровень оплаты труда сотрудников районного УВД (табл. 15), определить долю вариации заработной платы, обусловленную различиями в уровне образования сотрудников районного УВД.

Таблица 15

Образование	Средний уровень месячной заработной платы (тыс. руб.)	Количество сотрудников	Дисперсия заработной платы (тыс. руб.)
Среднее
Среднее специальное
Высшее (неюридическое)
Высшее юридическое

Решение. Вычисляем общее среднее значение, межгрупповую и среднюю внутригрупповую дисперсию:

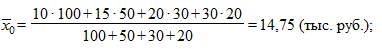
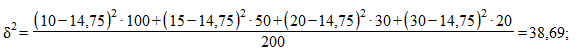
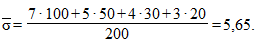
Тогда общая дисперсия равна:

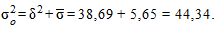
Следовательно, коэффициент детерминации равен:

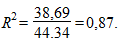
Полученный коэффициент детерминации показывает, что вариация в оплате труда на 87% зависит от уровня образования сотрудников районного УВД.