Средняя величина - это обобщающий показатель, который характеризует качественно однородную совокупность по определенному количественному признаку. Например, средний возраст лиц, осужденных за кражу.
В правовой статистике средние величины используют для характеристики:
- средних сроков рассмотрения дел данной категории;
- среднего размера иска;
- среднего числа ответчиков, приходящихся на одно дело;
- среднего размера ущерба;
- средней нагрузки судей и др.
Средняя величина - величина всегда именованная и имеет ту же размерность, что и признак у отдельной единицы совокупности. Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному варьирующему признаку, поэтому за всякой средней скрывается ряд распределения единиц этой совокупности по изучаемому признаку. Выбор вида средней определяется содержанием показателя и исходных данных для расчета средней величины. Все виды средних величин, используемые в статистических исследованиях, подразделяются на две категории: 1) степенные средние; 2) структурные средние. Первая категория средних величин включает: среднюю арифметическую, среднюю гармоническую, среднюю геометрическую и среднюю квадратическую. Вторая категория - это мода и медиана. При этом каждый из перечисленных видов степенных средних величин может иметь две формы: простую и взвешенную. Простая форма средней величины используется для получения среднего значения изучаемого признака, когда расчет осуществляется по несгруппированным статистическим данным, либо когда каждая варианта в совокупности встречается только один раз. Взвешенными средними называют величины, которые учитывают, что варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на соответствующую частоту. Иными словами, каждый вариант "взвешивают" по своей частоте. Частоту называют статистическим весом.
Средняя арифметическая простая - самый распространенный вид средней. Она равна сумме отдельных значений признака, деленной на общее число этих значений:
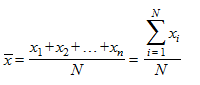 ,
,
где 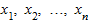 - индивидуальные значения варьирующего признака (варианты), а N - число единиц совокупности.
- индивидуальные значения варьирующего признака (варианты), а N - число единиц совокупности.
Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов:
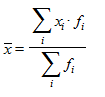 ,
,
где 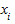 - значение, i-й варианты признака;
- значение, i-й варианты признака; 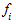 - частота i-й варианты.
- частота i-й варианты.
Таким образом, каждое значение варианты взвешивается по своей частоте, поэтому частоты иногда называют статистическими весами.
Замечание. Когда речь идет о средней арифметической величине без указания ее вида, подразумевается средняя арифметическая простая.
Пример. Рассчитать среднее число обвиняемых, приходящихся на одно уголовное дело, используя данные табл. 3.
Решение. Для расчета используем формулу средней арифметической взвешенной:
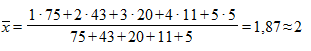 .
.
Таким образом, в среднем на одно уголовное дело приходится два обвиняемых.
Если вычисление средней величины производят по данным, сгруппированным в виде интервальных рядов распределения, то сначала надо определить серединные значения каждого интервала 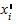 , после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, в которую вместо
, после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, в которую вместо 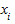 подставляют
подставляют 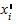 .
.
Пример. Данные о возрасте преступников, осужденных за совершение кражи, представлены в табл. 13.
Таблица 13
| Группы по возрасту (лет) | Количество человек |
| До 18 | |
| 18-28 | |
| 29-39 | |
| 40 и более |
Определить средний возраст преступников, осужденных за совершение кражи.
Решение. Для того чтобы определить средний возраст преступников на основе интервального вариационного ряда, необходимо сначала найти серединные значения интервалов. Так как дан интервальный ряд с открытыми первым и последним интервалами, то величины этих интервалов принимаются равными величинам смежных закрытых интервалов. В нашем случае величина первого и последнего интервалов равны 10. Далее находим серединные значения интервалов:
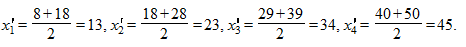
Теперь находим средний возраст преступников по формуле средней арифметической взвешенной:
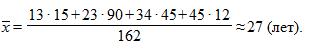
Таким образом, средний возраст преступников, осужденных за совершение кражи, приближенно равен 27 годам.
Средняя гармоническая простая представляет собой величину, обратную средней арифметической из обратных значений признака:
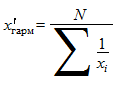 ,
,
где 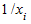 - обратные значения вариантов, а N-число единиц совокупности.
- обратные значения вариантов, а N-число единиц совокупности.
Пример. Для определения средней годовой нагрузки на судей районного суда при рассмотрении уголовных дел провели обследование нагрузки 5 судей этого суда. Затраты времени на одно уголовное дело оказались равными (в днях): 6,0, 5,6, 6,3, 4,9, 5,4. Найти средние затраты на одно уголовное дело и среднюю годовую нагрузку на судей данного районного суда при рассмотрении уголовных дел.
Решение. Для определения средних затрат времени на одно уголовное дело воспользуемся формулой средней гармонической простой:
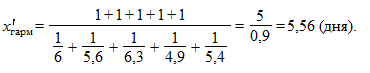
Тогда средняя годовая нагрузка (норма нагрузки) на судей данного районного суда при рассмотрении уголовных дел составит (расчет условный):
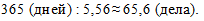
Если бы мы для определения средних затрат времени на одно уголовное дело воспользовались формулой средней арифметической простой, то получили бы:
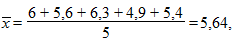
и средняя годовая нагрузка на одного судью составит:
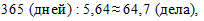
т.е. средняя нагрузка на судей оказалась меньше.
Проверим обоснованность такого подхода. Для этого воспользуемся данными о затратах времени на одно уголовное дело для каждого судьи и рассчитаем число уголовных дел, рассмотренных каждым из них за год. Получим соответственно:
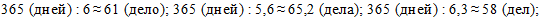
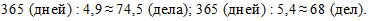
Теперь вычислим среднюю годовую нагрузку на судей данного районного суда при рассмотрении уголовных дел:
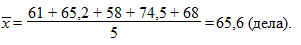
То есть средняя годовая нагрузка такая же, как и при использовании средней гармонической.
Таким образом, использование средней арифметической в данном случае неправомерно.
В тех случаях, когда известны варианты признака, их объемные значения (произведение варианты на частоту), но неизвестны сами частоты, применяется формула средней гармонической взвешенной:
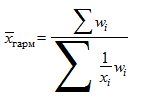 ,
,
где 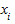 - значения вариантов признака, а
- значения вариантов признака, а 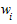 - объемные значения вариантов (
- объемные значения вариантов (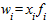 ).
).
Пример. Данные о цене единицы однотипного товара, произведенного различными учреждениями уголовно-исполнительной системы, и об объемах его реализации приведены в табл. 14.
Таблица 14
| Номер учреждения уголовно-исполнительной системы | Цена за единицу товара, руб. | Сумма от реализации товаров (выручка), руб. |
| 50 000 | ||
| 38 500 | ||
| 42 400 |
Найти среднюю цену реализации товара.
Решение. При расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам неизвестно количество реализованных единиц, но известны суммы реализаций товаров. Поэтому для нахождения средней цены реализованных товаров воспользуемся формулой средней гармонической взвешенной. Получаем:
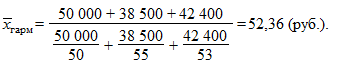
Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:
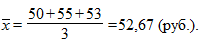
Средняя геометрическая вычисляется извлечением корня степени N из произведения всех значений вариантов признака:
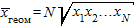 ,
,
где 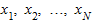 - индивидуальные значения варьирующего признака (варианты); N - число единиц совокупности.
- индивидуальные значения варьирующего признака (варианты); N - число единиц совокупности.
Этот вид средней используется для вычисления средних показателей роста рядов динамики.
Средняя квадратическая применяется для расчета среднеквадратического отклонения, являющегося показателем вариации, и будет рассмотрена ниже.
Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном (упорядоченном) ряду. Упорядочение единиц статистической совокупности может быть проведено по возрастанию или убыванию вариантов изучаемого признака.
Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда. Таким образом, медиана - это тот вариант ранжированного ряда, по обе стороны от которого в данном ряду должно находиться равное число единиц совокупности. Для нахождения медианы сначала необходимо определить ее порядковый номер в ранжированном ряду по формуле:
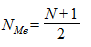 .
.
где N - объем ряда (число единиц совокупности).
Если ряд состоит из нечетного числа членов, то медиана равна варианте с номером 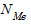 . Если же ряд состоит из четного числа членов, то медиана определяется как среднее арифметическое двух смежных вариант, расположенных в середине.
. Если же ряд состоит из четного числа членов, то медиана определяется как среднее арифметическое двух смежных вариант, расположенных в середине.
Пример. Дан ранжированный ряд 1, 2, 3, 3, 6, 7, 9, 9, 10. Объем ряда N = 9, значит 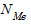 = (9 + 1): 2 = 5. Следовательно, Ме = 6, т.е. пятой варианте. Если дан ряд 1, 5, 7, 9, 11, 14, 15, 16, т.е. ряд с четным числом членов (N = 8), то
= (9 + 1): 2 = 5. Следовательно, Ме = 6, т.е. пятой варианте. Если дан ряд 1, 5, 7, 9, 11, 14, 15, 16, т.е. ряд с четным числом членов (N = 8), то 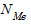 = (8 + 1): 2 = 4,5. Значит, медиана равна полусумме четвертой и пятой вариант, т.е. Ме = (9 + 11): 2 = 10.
= (8 + 1): 2 = 4,5. Значит, медиана равна полусумме четвертой и пятой вариант, т.е. Ме = (9 + 11): 2 = 10.
В дискретном вариационном ряду медиану определяют по накопленным частотам. Частоты вариант, начиная с первой, суммируются до тех пор, пока не будет превзойден номер медианы. Значение последней просуммированной варианты и будет медианой.
Пример. Найти медиану числа обвиняемых, приходящихся на одно уголовное дело, используя данные табл. 3.
Решение. В данном случае объем вариационного ряда N = 154, следовательно, 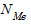 = (154 + 1): 2 = 77,5. Просуммировав частоты первой и второй варианты, получим: 75 + 43 = 118, т.е. мы превзошли номер медианы. Значит, Ме = 2.
= (154 + 1): 2 = 77,5. Просуммировав частоты первой и второй варианты, получим: 75 + 43 = 118, т.е. мы превзошли номер медианы. Значит, Ме = 2.
В интервальном вариационном ряду распределения сначала указывают интервал, в котором будет находиться медиана. Его называют медианным. Это первый интервал, накопленная частота которого превышает половину объема интервального вариационного ряда. Затем численное значение медианы определяется по формуле:
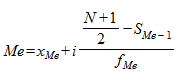 ,
,
где 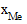 - нижняя граница медианного интервала; i - величина медианного интервала;
- нижняя граница медианного интервала; i - величина медианного интервала; 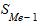 - накопленная частота интервала, который предшествует медианному;
- накопленная частота интервала, который предшествует медианному; 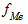 - частота медианного интервала.
- частота медианного интервала.
Пример. Найти медиану возраста преступников, осужденных за совершение кражи, на основе статистических данных, представленных в табл. 13.
Решение. Статистические данные представлены интервальным вариационным рядом, значит, сначала определим медианный интервал. Объем совокупности N = 162, следовательно, медианным интервалом является интервал 18-28, так как это первый интервал, накопленная частота которого (15 + 90 = 105) превышает половину объема (162: 2 = 81) интервального вариационного ряда. Теперь численное значение медианы определяем по приведенной выше формуле:
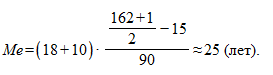
Таким образом, половина осужденных за совершение кражи младше 25 лет.
Модой (Мо) называют значение признака, которое наиболее часто встречается у единиц совокупности. К моде прибегают для выявления величины признака, имеющей наибольшее распространение. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Например, для дискретного ряда, представленного в табл. 3, Мо = 1, так как этому значению варианты соответствует наибольшая частота - 75. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. Его значение находят по формуле:
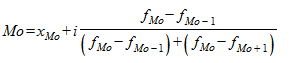 ,
,
где 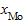 - нижняя граница модального интервала; i - величина модального интервала;
- нижняя граница модального интервала; i - величина модального интервала; 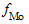 - частота модального интервала;
- частота модального интервала; 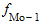 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 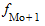 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Пример. Найти моду возраста преступников, осужденных за совершение кражи, данные о которых представлены в табл. 13.
Решение. Наибольшая частота соответствует интервалу 18-28, следовательно, мода должна находиться в этом интервале. Ее величину определяем по приведенной выше формуле:
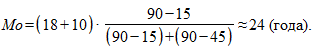
Таким образом, наибольшее число преступников, осужденных за совершение кражи, имеет возраст 24 года.
 2015-10-16
2015-10-16 3468
3468
