Прогнозирование с помощью моделей кривых роста

Более точные прогнозы можно получать с помощью моделей кривых роста. Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы:

1) предварительный анализ данных;

2) выбор в качестве моделей для прогнозирования одной или нескольких кривых, форма которых соответствует характеру изменения ряда динамики;

3) оценка параметров выбранных кривых;

4) проверка адекватности моделей прогнозируемому процессу и окончательный выбор кривой роста;

5) построение точечного и интервального прогнозов.

1. Предварительный анализ данных. На этом этапе производится:

- выявление аномальных наблюдений;

- проверка наличия тренда;

- выравнивание рядов динамики.

Поскольку наличие аномальных наблюдений приводит к искажению результатов анализа, то необходимо убедиться в отсутствии аномальных данных. Это можно сделать с помощью критерия Ирвина, описанного в п. 6.4. Аномальные наблюдения следует исключить из ряда динамики и заменить их средними арифметическими двух соседних значений.

Следующая процедура этапа предварительного анализа данных - выявление наличия тренда в развитии исследуемого показателя. Проверка гипотезы о наличии тренда проводится с помощью метода Фостера-Стюарта, описанного в п. 6.4.

И наконец, с помощью метода скользящей средней выполняем процедуру выравнивания исходного ряда динамики для определения модели развития динамики изучаемого явления.

2. Построение модели. Для решения задачи прогнозирования будущих значений исследуемого показателя в качестве моделей необходимо выбрать одну или несколько кривых роста, форма которых соответствует характеру изменения ряда динамики. В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания рядов динамики. Кривые роста условно могут быть разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают.

К первому типу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Среди кривых роста первого типа прежде всего следует выделить класс полиномов:

,

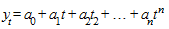где 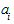(i = 0,1,..., n) - параметры многочлена, t - независимая переменная (время).

Оценки параметров в полиномиальной модели определяются методом наименьших квадратов, о котором мы уже говорили выше.

Отличительная черта полиномов - отсутствие в явном виде зависимости приростов от значений ординат (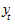). Коэффициенты полиномов невысоких степеней могут иметь конкретную интерпретацию в зависимости от содержания динамического ряда. Например, их можно трактовать как скорость роста (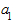), ускорение роста (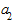), изменение ускорения (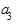), начальный уровень ряда при t = 0 (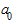). В статистических исследованиях чаще всего применяются полиномы не выше третьего порядка.

Для класса экспоненциальных кривых, в отличие от полиномов, характерной является зависимость приростов от величины самой функции. Эти кривые хорошо описывают процессы, имеющие "лавинообразный" характер, когда прирост зависит от достигнутого уровня функции. Простая экспоненциальная (показательная) кривая имеет вид:

.

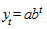Если b > 1, то кривая растет вместе с ростом t, и падает, если b < 1.

Параметр a характеризует начальные условия развития, а параметр b - постоянный темп роста. Действительно, темп роста равен 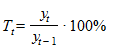. В данном случае 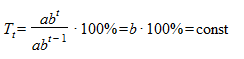. Соответственно и темпы прироста - постоянны, так как .

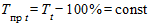Можно показать, что логарифм ординаты этой функции линейно зависит от t, для чего прологарифмируем выражение для данной функции:

.

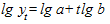Пусть 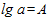; 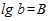. Тогда .

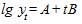Теперь для оценивания неизвестных параметров можем использовать метод наименьших квадратов.

Более сложным вариантом экспоненциальной кривой является логарифмическая парабола:

.

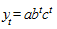Прологарифмировав, получим параболу:

.

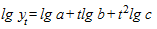Таким образом, оценку параметров логарифмической параболы можно опять осуществить с помощью метода наименьших квадратов.

Все рассмотренные выше типы кривых используются для описания монотонно возрастающих или убывающих процессов без "насыщения".

Ко второму классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются, например, в демографии. Функции, относящиеся ко второму классу, называются кривыми насыщения.

Когда процесс характеризуется "насыщением", его следует описывать при помощи кривой, имеющей отличную от нуля асимптоту. Примером такой кривой может служить модифицированная экспонента:

,

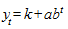где у = k является горизонтальной асимптотой.

Если параметр а отрицателен, то асимптота находится выше кривой, если 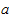положителен - то ниже. При решении практических задач часто можно определить значение асимптоты исходя из свойств прогнозируемого процесса. Иногда значение асимптоты задается экспертным путем. В этих случаях другие параметры кривой могут быть определены с помощью метода наименьших квадратов после приведения уравнения к линейному виду.

Таким образом, модифицированная экспонента хорошо описывает процесс, на развитие которого воздействует ограничивающий фактор, причем влияние этого воздействия растет вместе с ростом достигнутого уровня.

Если кривые насыщения имеют точки перегиба, то они относятся к третьему типу кривых роста - к S-образным кривым. Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, другой - с замедлением. Например, если воздействие ограничивающего фактора начинает сказываться только после определенного момента (точки перегиба), до которого процесс развивался по некоторому экспоненциальному закону, то для выравнивания используют S-образные кривые.

Наиболее известными из S-образных кривых являются кривая Гомперца и логистическая кривая, или кривая Перла-Рида.

Кривая Гомперца имеет вид

.

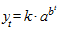Кривая несимметрична. Если 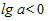, то кривая имеет S-образный вид, при этом асимптота, равная k, проходит выше кривой.

Если 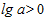, асимптота, равная k, лежит ниже кривой, а сама кривая изменяется монотонно: при b < 1 - монотонно убывает; при b > 1 - монотонно возрастает.

Уравнение логистической кривой получается путем замены в модифицированной экспоненте 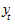обратной величиной :

.

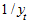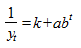Используется и другая форма записи уравнения логистической кривой:

.

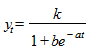При 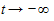ордината стремится к нулю, а при 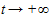к асимптоте, равной значению параметра k. Кривая симметрична относительно точки перегиба с координатами: 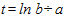, 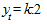. Логистическая функция возрастает сначала ускоренным темпом, затем темп замедляется и, наконец, рост почти полностью прекращается.

Таким образом, мы рассмотрели наиболее часто используемые в статистических исследованиях виды кривых роста. Выявленные особенности и свойства этих кривых могут существенно помочь при решении задачи выбора типа кривой.

Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста. Наиболее простой путь - это визуальный, опирающийся на графическое изображение динамического ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандартные преобразования ряда (например, выравнивание ряда), а потом подобрать функцию, отвечающую графику преобразованного ряда. В современных пакетах статистической обработки имеется богатый арсенал стандартных преобразований данных и широкие возможности для графического изображения, в том числе в различных масштабах. Все это позволяет существенно упростить для исследователя проведение данного этапа.

В статистической литературе описан метод последовательных разностей, помогающий при выборе кривых полиномиального типа. Этот метод применим при выполнении следующих предположений:

- уровни ряда динамики могут быть представлены в виде суммы детерминированной составляющей и случайной компоненты, подчиненной нормальному закону распределения со средним значением, равным 0, и постоянной дисперсией;

- интервалы между уровнями ряда динамики должны быть одинаковы.

Метод предполагает вычисление первых, вторых и последующих разностей уровней ряда:

;

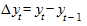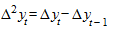
и т.д.

Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей, остающихся примерно равными друг другу, принимается за степень выравнивающего полинома.

В современных пакетах статистической обработки данных и анализа рядов динамики представлен широкий спектр кривых роста. Например, в пакете "Олимп", разработанном в МЭСИ и широко используемом в учебном процессе, реализованы 16 кривых роста. Причем возможны несколько режимов работы, удобных для пользователя. Можно среди этих кривых выбрать отдельную функцию и получить подробный протокол, включающий интервальные и точечные оценки параметров, характеристики остатков, прогноз. Можно выделить на экране несколько функций, тогда протокол будет содержать оценки параметров всех заказанных функций и значения критерия для каждой из них. В качестве критерия выбирается средняя квадратическая ошибка:

,

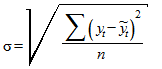где 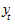- фактическое значение ряда, 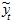- выровненное значение ряда, n - длина ряда.

В заключение отметим, что нет "жестких" рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполирования найденных закономерностей в будущее. Применение кривых роста должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде. Рассмотренные в данном разделе различные статистические приемы и методы могут помочь исследователю при осуществлении сложного выбора подходящей кривой роста.

3. Оценка качества построенных моделей. Проверка адекватности выбранных моделей реальному процессу (в частности, адекватности полученной кривой роста) строится на анализе случайной (остаточной) компоненты, т.е. расхождении уровней, рассчитанных по модели, и фактических наблюдений. Для этого исследуют ряд остатков, который может быть получен как отклонения фактических уровней ряда динамики (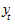) от выровненных, расчетных ():

.

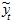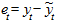При использовании кривых роста 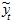вычисляют, подставляя в уравнения выбранных кривых соответствующие последовательные значения времени.

Принято считать, что модель адекватна описываемому процессу, если значения случайной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения.

При правильном выборе модели тренда отклонения от него будут носить случайный характер. Это означает, что изменение случайной компоненты не связано с изменением времени. Таким образом, по данным, полученным для всех моментов времени на изучаемом интервале, проверяется гипотеза о зависимости последовательности значений 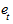от времени, или, что то же самое, о наличии тенденции в ее изменении. Поэтому для проверки данного свойства может быть использован, например, критерий Фостера-Стюарта.

Если модель тренда выбрана неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, так как они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок. В условиях автокорреляции эффективность оценок параметров модели, полученных по методу наименьших квадратов, будет снижаться, а следовательно, доверительные интервалы будут иметь мало смысла в силу своей ненадежности. Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является метод, предложенный Дарбиным и Уотсоном. С этой целью строится статистика Дарбина-Уотсона (d-статистика), в основе которой лежит формула:

.

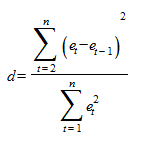При отсутствии автокорреляции статистика 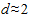, а при полной автокорреляции равна 0 или 4. Следовательно, оценки, получаемые по критерию, являются не точечными, а интервальными. Верхние и нижние критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции, зависят от количества уровней ряда динамики и числа независимых переменных модели. Авторами критерия значения этих границ определены для 1, 2,5 и 5% уровней значимости и даны в специальных таблицах. Значения границ для критерия Дарбина-Уотсона при 5%-ных уровне значимости приведены в табл. 22. 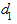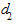В этой таблице и соответственно нижняя и верхняя доверительные границы критерия Дарбина-Уотсона; к - число переменных в модели; n - длина ряда динамики.

Таблица 22

n	к = 1	к = 2	к = 3
	d 1	d 2	d 1	d 2	d 1	d 2
	1,08	1,36	0,95	1,54	0,82	1,75
	1,1	1,37	0,98	1,54	0,86	1,73
	1,13	1,38	1,02	1,54	0,9	1,71
	1,16	1,39	1,05	1,53	0,93	1,69
	1,18	1,4	1,08	1,53	0,97	1,68
	1,2	1,41	1,1	1,54		1,68
	1,22	1,42	1,13	1,54	1,03	1,67
	1,24	1,43	1,15	1,54	1,05	1,66
	1,26	1,44	1,17	1,54	1,08	1,66
	1,27	1,45	1,19	1,55	1,1	1,66
	1,29	1,45	1,21	1,55	1,12	1,66
	1,3	1,46	1,22	1,55	1,14	1,65
	1,32	1,47	1,24	1,56	1,16	1,65
	1,33	1,48	1,26	1,56	1,18	1,65
	1,34	1,48	1,27	1,56	1,2	1,65
	1,35	1,49	1,28	1,57	1,21	1,65
	1,36	1,5	1,3	1,57	1,23	1,65
	1,37	1,5	1,31	1,57	1,24	1,65
	1,38	1,51	1,32	1,58	1,26	1,65
	1,49	1,51	1,33	1,58	1,27	1,65
	1,4	1,52	1,34	1,58	1,28	1,65
	1,41	1,52	1,35	1,59	1,29	1,65

Применение на практике критерия Дарбина-Уотсона основано на сравнении величины d, рассчитанной по приведенной выше формуле, с значениям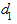и и 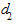, взятыми из таблицы.

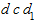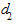При сравнении величины и возможны следующие варианты:

1) если d < 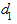, то гипотеза об отсутствии автокорреляции отвергается;

2) если d > 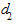, то гипотеза об отсутствии автокорреляции принимается;

3) если 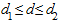, то нет достаточных оснований для принятия решений, т.е. величина попадает в область "неопределенности".

Рассмотренные варианты относятся к случаю, когда в остатках имеется положительная автокорреляция. Когда же расчетное значение d превышает 2, то можно говорить о том, что в 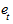существует отрицательная автокорреляция.

Для проверки отрицательной автокорреляции с критическими значениям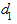и и 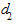сравнивается не сам коэффициент d, а 4 - d.

Замечание. Отметим, что большинство программных пакетов статистической обработки данных осуществляет расчет этого критерия (например, ППП "Олимп", "Statistica" и др.).

Для определения доверительных интервалов прогнозируемых значений показателя важное значение имеет свойство нормальности распределения остатков. Соответствие ряда остатков нормальному закону распределения можно проверить с помощью RS-критерия:

, ,

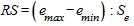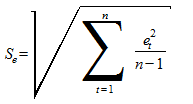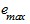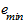где и - соответственно максимальный и минимальный уровни ряда остатков, а 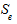- среднее квадратическое отклонение ряда остатков.

Если расчетное значение RS-критерия попадает между табулированными границами с заданным уровнем доверительной вероятности, то считают, что ряд остатков подчиняется нормальному распределению. В этом случае допустимо строить доверительный интервал прогноза.

Если все пункты проверки случайной компоненты дают положительный результат, то выбранная трендовая модель является адекватной реальному ряду динамики, и следовательно, ее можно использовать для построения прогнозных оценок. В противном случае - модель нужно улучшать.

Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели. Поэтому, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих не только адекватность модели, но и ее точность. О точности прогноза можно судить по величине ошибки (погрешности) прогноза. Ошибка прогноза - величина, характеризующая расхождение между фактическим и прогнозным значением показателя. Абсолютная ошибка прогноза определяется по формуле:

,

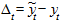где 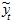- прогнозное значение показателя, 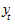- фактическое значение.

Эта характеристика имеет ту же размерность, что и прогнозируемый показатель, и зависит от масштаба измерения уровней временного ряда.

На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя:

.

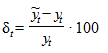Из приведенных формул видно, что если абсолютная и относительная ошибка больше 0, то это свидетельствует о "завышенной" прогнозной оценке, если меньше 0, то прогноз был занижен.

Очевидно, что все указанные характеристики могут быть вычислены после того, как период упреждения уже окончился и имеются фактические данные о прогнозируемом показателе. В противном случае для оценки точности трендовой модели используют коэффициент детерминации

,

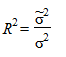где 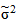- дисперсия данных, полученная по трендовой модели

;

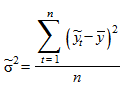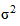- дисперсия исходных данных уровней ряда динамики

;

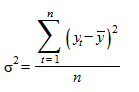n - число уровней ряда динамики.

Трендовая модель считается адекватной изучаемому процессу и отражает тенденцию его развития во времени при значениях 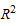, близких к 1.

4. Построение точечных и интервальных прогнозов. Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения, т.е. t = n + 1, n + 2,... Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя. Однако точное совпадение прогностических точечных оценок, полученных путем экстраполяции тенденции по кривым роста, и фактических данных маловероятно. Возникновение соответствующих отклонений объясняется следующими причинами:

1) погрешностью оценивания параметров кривых;

2) погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени.

3) выбранная для прогнозирования кривая не является наилучшей; можно подобрать другую кривую, которая даст более точные результаты.

Поэтому на практике в дополнение к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, т.е. вычислить прогноз интервальный. Интервальные прогнозы строятся на основе точечных прогнозов. Доверительным интервалом называется такой интервал, относительно которого можно с заранее выбранной вероятностью утверждать, что он содержит значение прогнозируемого показателя. Ширина интервала зависит от качества модели, т.е. степени ее близости к фактическим данным, числа наблюдений, периода упреждения и выбранного пользователем уровня доверительной вероятности.

Доверительный интервал, учитывающий неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, определяется в виде:

,

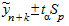где n - длина ряда динамики; к - период упреждения; 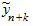- точечный прогноз на момент n + к; 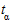- значение t-статистики Стьюдента; 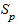- средняя квадратическая ошибка прогноза.

Предположим, что тренд характеризуется прямой

.

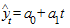Так как оценки параметров определяются по совокупности, представленной рядом динамики, то они содержат погрешность. Погрешность параметра 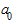приводит к вертикальному сдвигу прямой, а погрешность параметра 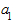- к изменению угла наклона прямой относительно оси абсцисс. С учетом разброса конкретных реализаций относительно линий тренда, дисперсию 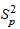можно представить в виде:

,

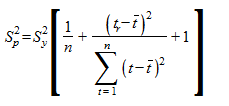где 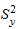- дисперсия отклонений фактических наблюдений от расчетных; 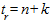- время упреждения, для которого делается экстраполяция; t - порядковый номер уровней ряда, t = 1, 2,..., n, 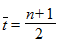- порядковый номер уровня, стоящего в середине ряда.

Тогда доверительный интервал можно представить в виде:

.

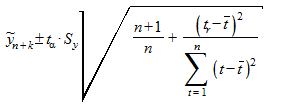Аналогичное выражение можно получить и для полинома второго порядка:

.

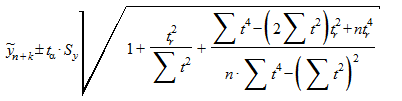Дисперсия отклонений фактических наблюдений от расчетных определяется выражением:

,

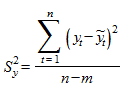где 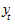- фактические значения уровней ряда; 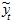- расчетные значения уровней ряда, n - длина временного ряда, m - число оцениваемых параметров выравнивающей кривой.

Таким образом, ширина доверительного интервала зависит от доверительной вероятности, периода упреждения, среднего квадратического отклонения от тренда и степени полинома. Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении 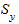, так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения.

Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяются аналогичным способом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы.

По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).

Пример. Построить прогноз на 2009 г. преступлений в сфере компьютерных технологий с помощью моделей кривых роста, используя статистику зарегистрированных преступлений за 1997-2008 гг. (табл. 23).

Таблица 23