Интервал

Вернемся к понятию интервала между событиями. В нештрихованной системе отсчета квадрат интервала равен 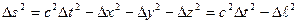. Будем считать, что оба события происходят с одной и той же частицей. Тогда

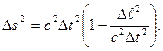
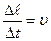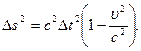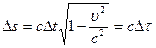Но - скорость частицы, поэтому , или , где 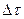- промежуток собственного времени частицы между событиями.

Мы говорили, что 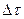и c являются инвариантами, следовательно, интервал 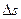равен произведению двух инвариантов и также является инвариантом, т.е. его величина не зависит от выбора системы отсчета и во всех инерциальных системах отсчета одинакова.

Если 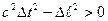, интервал называется вещественным. В этом случае существует такая система отсчета 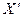, в которой 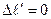, т.е. события, разделенные вещественным интервалом, могут быть пространственно совмещенными. Однако не существует систему отсчета, в которой 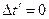, т.е. события, разделенные вещественным интервалом, ни в коем случае не могут быть одновременными. Поэтому вещественный интервал называется времениподобным.

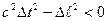Если , интервал называется мнимым, для таких интервалов существует система 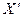, в которой 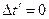, т.е. события оказываются одновременными. Однако не существует системы, в которо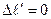й (при 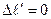интервал будет вещественным), т.е.события, разделенные мнимым интервалом, не могут оказаться пространственно совмещенными. Такой интервал называется пространственноподобным, при этом 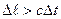, поэтому события не могут воздействовать друг на друга и не могут быть причинно связанными друг с другом, так как не существует воздействий, распространяющихся со скоростью, большей скорости света, порядок следования событий может быть произвольным.

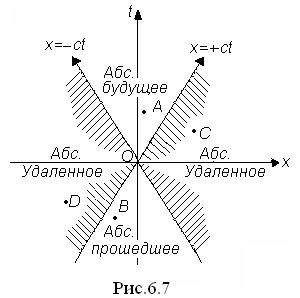
Возьмем мировую точку О некоторого события за начало отсчета времени и координат. Проведем в четырехмерном пространстве через эту точку взаимно перпендикулярные оси x,y,z,t. На рис. 6.7 представлена плоскость x,t, для которой y= 0, z= 0. Движение частицы со скоростью 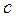, происходящее в трехмерном пространстве вдоль оси x, изображено на рисунке прямыми 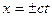. Скорость частицы не может превышать 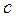, поэтому мировые линии всех частиц, проходящий при своем движении через мировую точку О, будут лежать в пределах незаштрихованной области. В четырехмерном пространстве этой области соответствует конус, осью которого является t. Образующие конуса представляют собой мировые линии световых сигналов. Поэтому его называют световым конусом.

Для любой мировой точки А, лежащей в области, названной на рис.6.6 абсолютно будущей, 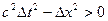и интервал 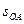между событиями О и А – времениподобный, причем в выбранной нами системе отсчета 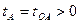. Если брать системы отсчета, скорость которых 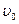относительно нашей системы меняется непрерывно, будет непрерывно меняться и промежуток времени 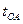. Однако, ни в одной системе отсчета 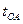не может быть равным нулю (два события, разделенные времениподобным интервалом, ни в какой системе отсчета не могут быть одновременными) Следовательно, не существует и таких систем отсчета, в которых 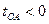(чтобы стать отрицательным, 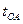должен при непрерывном изменении 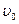измениться скачком). Таким образом, во всех системах отсчета событие А будет происходить позже события О.

Для любой мировой точки B, лежащей в абсолютно прошедшей области, 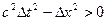, т.е. интервал 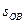-времениподобный, однако 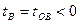и во всех системах отсчета событие B предшествует событию О.

Для любого события C или D, мировая точка которого лежит в абсолютно удаленных областях, 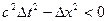, и интервалы 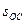и 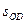- пространственноподобные. В любой системе отсчета события O и C, или O и D происходят в разных точках пространства. Понятие одновременности этих событий является относительным. В одних системах отсчета событие C (или D) происходит позже, а в других раньше события O. Имеется одна система отсчета, в которой событие C (или D) происходит одновременно с O).

6 .6. ПРЕОБРАЗОВАНИЕ СКОРОСТЕЙ В РЕЛЯТИВИСТСКОЙ КИНЕМАТИКЕ

Рассмотрим движение материальной точки (рис.6.8). В системе X положение точки 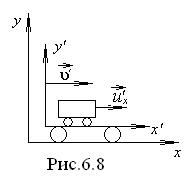определяется в каждый момент времени t координатами x,y,z. Выражения 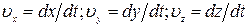представляют собой проекции вектора скорости точки на соответствующие оси в системе отсчета X. В системе 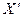положение материальной точки характеризуется в каждый момент времени 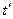координатами 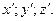Проекции вектора скорости относительно 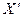на эти оси определяются выражениями 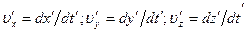. Из формул (6.2) получаем

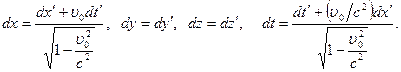
Разделив первые три равенства на четвертое, получаем формулы для преобразования скоростей при переходе их одной системы отсчета в другую:

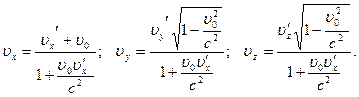(6.3)

При 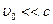эти соотношения переходят в преобразования Галилея в классической механике. Обратные преобразования имеют вид:

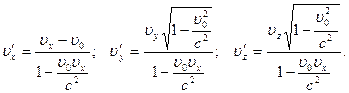
Если тело движется параллельно оси x, его скорость 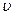относительно системы X совпадает с 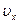, а скорость 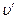относительно системы 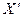- с 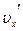. В этом случае закон сложения скоростей принимает вид

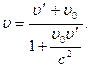(6.4)

Если скорость частицы в одной системе отсчета 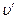= c, то в другой системе, согласно (6.4) эта скорость равна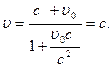

Мы получили, что скорость света одинакова во всех инерциальных системах отсчета.