Парадоксы релятивистской кинематики: сокращение длины и замедление времени в движущихся системах отсчета

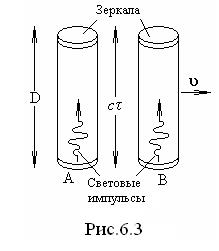
Применим оба принципа теории относительности к простой разновидности часов – световым часам. Они представляют собой два обычных зеркала, установленных параллельно друг другу на расстоянии 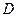(рис.6.3). Такое устройство может служить своего рода часами, если поверхности зеркал абсолютно отражающие и короткий световой импульс бегает между ними в прямом и обратном направлениях. Пусть 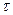- время, за которое импульс света, отразившись от нижнего зеркала, достигнет верхнего. Часы “тикают” всякий раз, когда свет отражается от зеркала. Рассмотрим две пары вполне идентичных часов 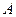и 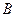, причем частота их синхронизована и период тиканья равен 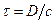. Часы 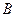движутся вправо со скоростью 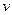. Останется ли длина движущихся часов 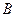такой же, как у часов 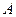? Пусть на конце часов 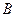имеется небольшая кисточка с краской. Когда часы 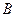проходят мимо часов 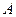, эта кисточка оставляет на часах 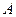метку, и, если метка приходится на край часов 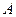, то это означает, что длина часов 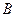не изменилась. Если же метка окажется ниже края часов 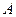, то длина часов 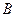при движении сократилась. Предположим, что именно последний случай и реализован в действительности. Тогда наблюдатель, движущийся вместе с часами 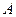, увидит, что движущиеся часы 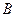стали короче. С другой стороны, с точки зрения наблюдателя 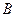движущиеся относительно него световые часы окажутся длиннее. Однако, согласно принципу относительности, оба наблюдателя совершенно равноправны и оба должны наблюдать один и тот же эффект. Это возможно лишь в том случае, когда обоим наблюдателям обе пары часов кажутся одной и той же длины.

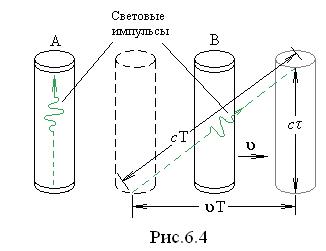Рассмотрим наблюдателя 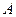(рис.6.4). Ему путь светового луча от одного края часов 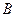до другого будет представляться более длинным, чем в часах 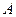(световой импульс относительно наблюдателя 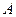движется по диагонали со скоростью света 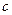). Следовательно, с точки зрения наблюдателя 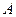световому импульсу в часах 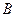понадобится больше времени для того, чтобы достичь верхнего зеркала, чем световому импульсу в часах 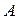. Обозначим этот больший промежуток времени 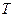, тогда длина диагонали равна 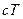, и по теореме Пифагора 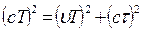, отсюда

.

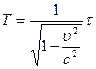В теории относительности множитель, стоящий перед 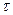, встречается очень часто и обозначается .

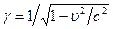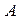Наблюдатель видит тиканье часов 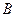через время 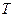, а тиканье своих часов 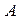через время 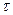. Таким образом, любой наблюдатель обнаруживает замедление хода движущихся часов в 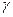раз по сравнению с точно такими же, но находящимися в покое часами. Величина 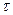называется собственным временем. Это измеренный наблюдателем промежуток времени между двумя событиями, которые наблюдатель видит в одной и той же точке пространства. Тогда 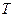- промежуток времени между теми же событиями, но измеренный движущимся наблюдателем по его собственным часам. Собственное время 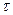– это время, измеренное наблюдателем, движущимся вместе с часами. Оно одинаково во всех инерциальных системах отсчета, т.е. является инвариантом.

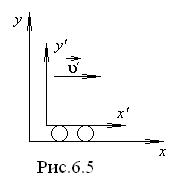
Предположим теперь, что наблюдатель X решил измерить длину метровой линейки, покоящейся относительно штрихованной системы координат, сама же система координат 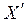движется относительно нештрихованной X со скоростью 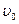(рис.6.5). Концы этой линейки закреплены в точках 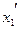и 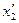, тогда из преобразований Лоренца получаем:

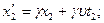
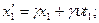
Длина линейки в штрихованной системе (длина покоящейся линейки) равна 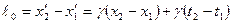. Чтобы наблюдатель 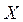правильно измерил в своей системе отсчета длину движущегося предмета, он должен постараться отметить положения концов линейки в моменты времени, которые он считает совпадающими: 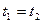, поэтому 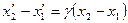. Очевидно, 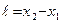- длина линейки, которую измерит наблюдатель X. Относительно этого наблюдателя линейка движется со скоростью 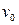. Тогда 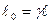, или 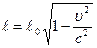- длина движущейся линейки в 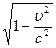раз меньше длины этой же линейки в покое. Данный факт получил название лоренцева сокращения длины.