Автор: – Начнем обсуждение самого простого неравномерного движения – движения с постоянным ускорением. Такое движение называют равноускоренным.
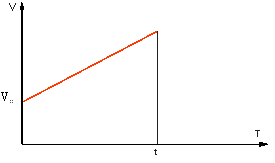
Рис. 1.2.1
График зависимости V(t) для этого случая показан на рис.1.2.1. Промежуток времени Δt в формуле (1.4) можно брать любой. Отношение ΔV/Δt от этого не зависит. Тогда ΔV=аΔt. Применяя эту формулу к промежутку от tо = 0 до некоторого момента t, можно написать выражение для скорости:
V(t)=V0 + at. (1.5)
Здесь V0 – значение скорости при tо = 0. Если направления скорости и ускорения противоположны, то говорят о равнозамедленном движении (рис. 1.2.2).
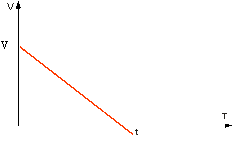
Рис. 1.2.2
При равнозамедленном движении аналогично получаем
V(t) = V0 – at.
Разберём вывод формулы перемещения тела при равноускоренном движении. Заметим, что в этом случае перемещение и пройденный путь – одно и тоже число.
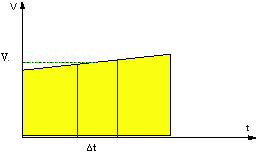
Рис.1.2.3
Рассмотрим малый промежуток времени Δt. Из определения средней скорости Vcp = ΔS/Δt можно найти пройденный путь ΔS = VcpΔt. На рисунке видно, что путь ΔS численно равен площади прямоугольника с шириной Δt и высотой Vcp. Если промежуток времени Δt выбрать достаточно малым, средняя скорость на интервале Δt совпадет с мгновенной скоростью в средней точке. ΔS ≈ VΔt. Это соотношение тем точнее, чем меньше Δt. Разбивая полное время движения на такие малые интервалы и учитывая, что полный путь S складывается из путей, пройденных за эти интервалы, можно убедиться, что на графике скорости он численно равен площади трапеции:
S= ½·(V0 + V)t,
подставляя (1.5), получим для равноускоренного движения:
S = V0t + (at2/2) (1.6)
Для равнозамедленного движения перемещение L вычисляется так:
L= V0t–(at2/2).
Разберем задачу 1.3.
Пусть график скорости имеет вид, изображенный на рис. 1.2.4. Нарисуйте качественно синхронные графики пути и ускорения от времени.
Студент: – Мне не приходилось встречаться с понятием «синхронные графики», я также не очень представляю, что значит «нарисовать качественно».
Автор: – Синхронные графики имеют одинаковые масштабы по оси абсцисс, на которой отложено время. Расположены графики один под другим. Удобны синхронные графики для сопоставления сразу нескольких параметров в один момент времени. В этой задаче мы будем изображать движение качественно, т. е. без учета конкретных числовых значений. Для нас вполне достаточно установить: убывает функция или возрастает, какой вид она имеет, есть ли у нее разрывы или изломы и т. д. Думаю, для начала нам следует рассуждать вместе.
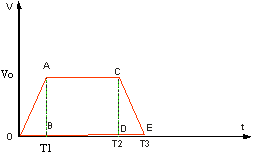
Рис.1.2.4
Разделим все время движения на три промежутка ОВ, BD, DE. Скажите, какой характер носит движение на каждом из них и по какой формуле будем вычислять пройденный путь?
Студент: – На участке ОВ тело двигалось равноускоренно с нулевой начальной скоростью, поэтому формула для пути имеет вид:
S 1 (t) = at2/2.
Ускорение можно найти, разделив изменение скорости, т.е. длину АВ, на промежуток времени ОВ.
Автор: – Хорошо. Теперь рассмотрите другие временные участки – ВD и DЕ.
Студент: – На участке ВD тело движется равномерно со скоростью V0, приобретенной к концу участка ОВ. Формула пути – S = Vt. Ускорения нет.
Автор: – Следует уточнить, что равномерное движение началось не в начальный момент времени, а в какой-то t 1. К этому времени тело уже прошло путь at 12/2. Кроме того, за начало отсчета времени необходимо взять момент t 1. Зависимость пути от времени имеет следующий вид:
S 2 (t) = at12/2 + V 0 (t– t1).
Учитывая это пояснение, напишите формулу для пути на участке DE.
Студент: – На последнем участке движение равнозамедленное. Буду рассуждать так. До момента времени t 2 тело уже прошло расстояние S2 = at12/2 + V(t2– t1).
К нему надо добавить выражение для равнозамедленного случая, учитывая, что время отсчитывается от значения t2 получаем пройденный путь, за время t – t2:
S3=V 0 (t–t2)–[a1(t–t2)2]/2.
Предвижу вопрос о том, как найти ускорение a 1. Оно равно СD/DE. В итоге получаем путь, пройденный за время t>t2
S (t)= at12/2+V 0 (t–t1)– [a1(t–t2)2]/2.
Автор: – Верно. Переходите к построению графиков.
Студент: – На первом участке имеем параболу с ветвями, направленными вверх. На втором – прямую, на последнем – тоже параболу, но с ветвями вниз.
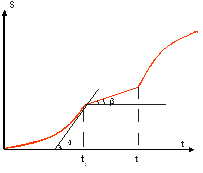
Рис. 1.2.6
Автор: – Ваш рисунок имеет неточности. График пути не имеет изломов, т. е. параболы следует плавно сопрягать с прямой. Мы уже говорили, что скорость определяется тангенсом угла наклона касательной. По Вашему чертежу получается, что в момент t1 скорость имеет сразу два значения. Если строить касательную слева, то скорость будет численно равна tg α, а если подходить к точке справа, то скорость равна tg β. Но в нашем случае скорость – непрерывная функция. Противоречие снимается, если график построить так.
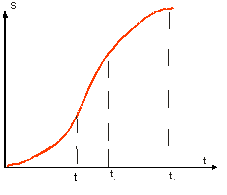
Рис. 1.2.7
Есть еще одно полезное соотношение между S, a, V и V 0. Будем предполагать, что движение происходит в одну сторону. В этом случае перемещение тела от начальной точки совпадает с пройденным путём. Используя (1.5), выразите время t и исключите его из равенства (1.6). Так Вы получите эту формулу.
Студент: – V(t) = V0 + at, значит,
t = (V– V0)/a,
S = V0t + at2/2 = V0(V– V0)/a + 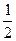 a[(V– V0)/a]2 =
a[(V– V0)/a]2 = 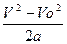 .
.
Окончательно имеем:
S = 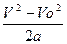 . (1.6а)
. (1.6а)
История.
Однажды во время обучения в Геттингене Нильс Бор плохо подготовился к коллоквиуму, и его выступление оказалось слабым. Бор, однако, не пал духом и в заключение с улыбкой сказал:
– Я выслушал здесь столько плохих выступлений, что прошу рассматривать моё как месть.
 2015-10-16
2015-10-16 11017
11017
