Физическая модель. Понятие скорости и ускорения

Как ученикам преуспеть?

Догонять тех, кто впереди,

и не ждать тех, кто позади.

Аристотель

Из-за сложности физического явления мы вынуждены его упрощать, огрублять, отказываться от несущественных деталей, сохраняя самые характерные и важные черты изучаемого объекта. В физике пока нет ни одной безупречной модели, и ученые постоянно стремятся усовершенствовать свои представления, особенно когда появляются экспериментальные результаты, указывающие на неадекватность предыдущих моделей.

Модель – это искусственно созданный объект в виде схемы, физических конструкций, знаковых форм или формул, который, будучи подобен исследуемому объекту (или явлению), отображает и воспроизводит в более простом и огрубленном виде структуру, свойства, взаимосвязи и отношения между элементами этого объекта.

Как правило, модель относительно проста и сохраняет структурные сходства изучаемого явления, т. е. изоморфна ему. Термин теория значительно шире: она рассматривает явление более детально, и с её помощью можно с достаточной математической точностью решать конкретные задачи. Когда модель получает свое развитие и становится достаточно полнотой, а также когда расчёты хорошо согласуются с экспериментом, говорят, что на ее основе построена теория, например, теория вещества или волновая теория света. Мы будем часто пользоваться понятием закон, под которым ученые обычно понимают краткие и достаточно общие утверждения относительно характера явлений природы (например, утверждение о сохранении и превращении энергии).

Теперь давайте вспомним некоторые понятия, характеризующие движение материальной точки. Кстати, а что такое материальная точка?

При описании полета пули мы часто пренебрегаем размерами пули. Движение планет можно описывать как материальные точки, т. к. их размеры хоть и очень большие (по земным меркам), но они намного меньше расстояния до Солнца.

Подводя итог, дадим определение. Материальной точкой называется модель тела, размеры и форма которого несущественны при заданных условиях.

Автор: – Попробуем изобразить известные в науке размеры материальных тел на одном рисунке.

Студент: – Я даже не представляю, как это можно сделать. Я читал о том, что ученые примерно вычислили размер Вселенной, но как на одном рисунке поместить, допустим, еще и атом, я не знаю.

Автор: – Для этого используется так называемая логарифмическая шкала. Пусть нам необходимо изобразить число Х =10ⁿ. На логарифмической шкале отмечают положение показателя степени. Таким образом, число Х на логарифмической шкале будет иметь координату n. Для нашей задачи эта шкала незаменима. Сейчас мы посмотрим, как весь мир от галактик до атомов поместится на небольшом отрезке. Итак, будем отмечать характерные размеры интересующих нас объектов, зная порядок их величины, т. е., имея размер в виде 10ⁿ м, отметим показатель степени n на логарифмической шкале.

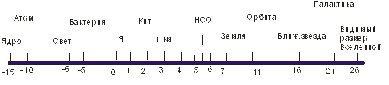
Рис. 1.1.1

Эта шкала отражает размеры всего известного в науке: от микроструктуры атома до Вселенной. Человек, находящийся в среднем диапазоне размеров, открывает порядок и закономерности, которые связывают поведение атомов с природой галактик. Исследуя как микромир, так и макромир, человек лучше осознает себя в этом мире. Оказывается, в нашей психике заложены подобия многих явлений природы. Надо только уметь их сопоставить.

Студент: – Это действительно прикольно. На таком небольшом отрезке расположилось все, о чем мы знаем. И эта картинка вполне информативна.

Автор: – Попробуйте соотнести размеры атома и ядра.

Студент: – Атом больше ядра в 10^–10: 10^–15 = 10⁵ раз. Это можно сравнить с соотношением размеров Новосибирской области (для НСО характерны расстояния ≈ 5·10⁵ м) и аудиторной доски в нашем колледже.

Автор: – На рисунке 1.1.1 мы изобразили первую физическую «декорацию» (модель), с помощью которой можно рассуждать о весьма сложных природных явлениях. Но в науке приняты свои термины, поэтому слово «декорация» мы больше применять не будем, а заменим его термином «модель».

Рассмотрим понятие средней скорости. Их два, но они не эквивалентны.

Определение I. Средняя скорость за промежуток времени Δt есть V_ср = ΔS/Δt, где ΔS – путь, пройденный за промежуток Δt. Как видим, из этого определения следует, что средняя скорость – скалярная величина, т. к. пройденный путь – это число. При таком определении средней скорости вполне корректно говорить о средней скорости автомобиля, равномерно движущегося по кольцевой дороге. Однако есть и другое, «векторное», определение средней скорости.

Определение II. Средняя скорость за промежуток времени Δt есть 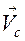= Δ 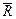/Δt, где Δ 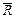– перемещение за промежуток Δt.

Как ни обидно, но, в соответствии с этим определением, средняя скорость нашего гипотетического автомобиля за полный период обращения по кольцевой дороге равна нулю. Потому что в данном случае средняя скорость – это вектор.

В каждом конкретном случае необходимо уточнять, о какой именно скорости идет речь.

Но следующий пример лишен этих нюансов, т. к. в нем мы рассмотрим одномерное движение в одну сторону. При этом вполне можно отождествить пройденный путь и перемещение.

Задача 1.1. На рис. 1.1.2 представлена зависимость пройденного пути S (м) от времени t (с). Чему равна средняя скорость за первые две секунды и за первые три секунды?

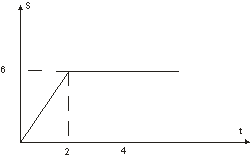
Рис. 1.1.2

Если в задаче встречается несколько временных интервалов, на каждом из которых тело имеет свою постоянную скорость, то среднюю скорость можно вычислить так:

V_ср = (V₁ Δt₁ + V₂ Δt₂ +…)/(Δt₁ + Δt₂+…),

где V₁ и Δt₁, V₂ и Δt₂ – соответственно, скорость и время в пути на первом участке, втором участке и т. д.

В таком случае средняя скорость за первые две секунды равна 3 м/с, а за первые три секунды – 2 м/с.

Следует помнить, что средняя скорость не может быть определена, если не указан временной промежуток усреднения. Важно не путать это понятие со средним арифметическим, хотя бывают случаи, когда они совпадают.

Для тренировки решите

задачу 1.2.

Первую половину пути тело двигалось равномерно со скоростью V₁ = 20 м/с, а вторую – со скоростью V₂ = 30 м/с. Чему равна средняя скорость за все время движения?

Студент: – Первое желание сразу ответить (20 + 30)/2 = 25 м/с. Но я помню Ваше замечание о том, что средняя скорость не есть среднее арифметическое скоростей. Поэтому буду действовать последовательно. Обозначу пройденный путь S. На первую половину пути тело затратило время Δt₁ = 0,5S/V₁, на вторую – Δt₂ = 0,5S/V₂.

Разделим весь путь на полное время:

V_ср = S/(Δt₁ + Δt₂)=2V₁V₂ /(V₁ + V₂) = 24 м/с.

Действительно, не совпадает со средним арифметическим.

Автор: – Попробуйте предположить, при каком движении средняя скорость тела в точности совпадет со средним арифметическим значением промежуточных скоростей.

Студент: – Кажется, я догадался. Если Δt₁ и Δt₂ будут равны, то ◄V_ср = S/(2Δt₁) = (V₁ + V₂)Δt₁/(2Δt₁) = 25 м/с►.

Для удобства здесь и далее мы будем оформлять ответ задачи специальными значками ◄►.

Автор: – Перейдем к понятию мгновенная скорость.

Студент: – По самому смыслу этого понятия ясно, что это скорость в данный момент времени.

Автор: А как ее вычислить? Мы же понимаем, что необходимо разделить какой-то путь на какое-то время.

Студент: – Можно выбрать какой-нибудь малый промежуток времени Δt: от данного момента t до t + Δt. Пусть за этот промежуток тело прошло путь ΔS. Если Δt выбран достаточно малым, то отношение ΔS/Δt и будет представлять собой то, что называют скоростью тела в момент t.

Автор: – Что значит «достаточно малый» промежуток времени? Малый по сравнению с чем: с годом, минутой, секундой?

Студент: – Пока я затрудняюсь ответить.

Автор: – Для правильного ответа нам понадобятся некоторые сведения из теории пределов. Составим последовательность значений средних скоростей за промежутки времени от t до t + Δt, выбирая все меньшие значения Δt. Предел этой последовательности при Δt, стремящемся к нулю, и есть скорость в момент t. Если известна зависимость пути от времени S(t), то скорость в момент t определятся выражением

V(t)= 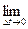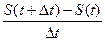. (1.1.1)

Другими словами, надо составить последовательность средних скоростей за промежутки от t до t+Δt, выбирая все меньшие значения Δt.

V(t)= 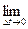V_ср.

Студент: – Я читал, что так определяется производная функции.

Автор: – Верно, т. е. V(t)= S'(t)≡dS/dt.

Студент: – А нельзя ли определить мгновенную скорость, не прибегая к дифференцированию?

Автор: – Строго говоря, нельзя. Подводя итог, приведём формулу для понятие мгновенной скорости. В этом случае в числителе выражения (1.1.1) пишут вектор перемещения. Таким образом, мгновенная скорость – это производная от перемещения по времени.

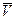(t)= Δ 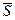(t)/Δt. (1.1.2)

Кроме того, следует пояснить очень полезную геометрическую интерпретацию мгновенной скорости. Рассмотрим некоторый график перемещения S(t) для простоты – в одномерном случае.

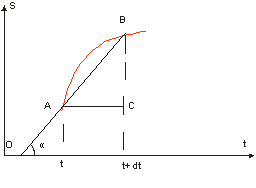
Рис. 1.1.3

Выберем два момента времени t и t + Δt. Средняя скорость на промежутке от t до t + Δt есть [S(t + Δt) – S(t)]/Δt. Из треугольника АВС видим, что это отношение есть tg α, где α – угол наклона секущей АВ к оси абсцисс. При Δt → 0 секущая превратится в касательную, а средняя скорость – в мгновенную. Таким образом, величина мгновенной скорости в данный момент времени может быть численно определена через тангенс угла наклона касательной, проведенной к графику перемещения от времени.

Студент: – Такое определение мгновенной скорости весьма наглядно: чем больше скорость, тем круче идет график пути.

Автор: – Используя график пути на рис. 1.1.4, найдите те моменты, когда мгновенная скорость равна средней скорости за все время движения.

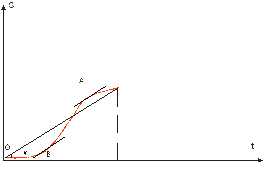
Рис. 1.1.4

Студент: – Средняя скорость за все время движения есть пройденный путь, деленный на затраченное время, и равна tg α. Нам необходимо найти такие точки на графике, тангенс угла наклона касательных в которых совпадет с tg α. Из рисунка видно, что это точки А и В.

Автор: – А может ли мгновенная скорость совпадать со средней в течение всего периода движения?

Студент: – Может, если движение равномерное. График пути в этом случае – прямая линия.

Автор: – Правильно. Перейдем к понятию «ускорение». Вся предыдущая логика наших рассуждений сохранится, только обозначения будут другими.

Студент: – В школе мы проходили, что ускорение есть скорость изменения скорости, оно существует при неравномерном движении тела. Если ускорение постоянно, то говорят о равноускоренном движении частицы.

Автор: – Всё это так. Однако дадим более строгое определение ускорения. Во-первых, для прямолинейного движения средним ускорением за промежуток времени Δt называют отношение изменения скорости к этому промежутку времени.

а_ср= ΔV/Δt.

Для прямолинейного движения ускорение (или мгновенное ускорение) в момент времени t есть предел последовательности средних ускорений за промежутки от t до t + Δt, вычисленные при Δt, стремящемся к нулю.

a(t)= 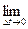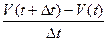(1.3)

Студент: – Действительно, сравнивая с (1.1.2), видим, что ускорение тела выражается через приращение его скорости так же, как выражалась скорость через приращение пути.

Автор: – Вы правы, скорость – это производная от перемещения по времени, а ускорение – производная скорости по времени. А как вы думаете, может ли в некоторый момент времени скорость тела быть нулевой, а ускорение нет?

Студент: – Так сразу и не скажешь.

Автор: – Попробуем рассуждать вместе. Вы предварительно знакомы с движением в поле тяжести и знаете, что в любой момент времени тело, брошенное вверх, испытывает ускорение g. Однако в верхней точке полета скорость равна нулю. Графически это можно понять из того, что если функция V(t) в какой-то точке равна нулю, вовсе не обязательно, что касательная в этой точке горизонтальна. Более того, сами направления скорости и ускорения могут не совпадать. Приведите пример.

Студент: – При торможении лифта, двигавшегося вверх. Скорость направлена вверх, а ускорение замедляет ее, значит, направлено вниз.

Автор: – Правильно. В заключение уточним, что ускорение величина – векторная, и для криволинейного движения необходимо давать определение в векторном виде:

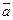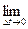
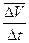= . (1.4)

Из этого определения следует интересный вывод: если скорость не меняется по модулю, а меняется только по направлению, то ускорение не равно нулю. Но к этому свойству мы вернемся, когда будем обсуждать движение по окружности.

Чтобы наши диалоги были не очень утомительными (и для читателей тоже), будем завершать каждый параграф занимательными историями из жизни великих ученых. Возможно, для некоторых они будут поучительными.

История.

Эйнштейн был в гостях у своих знакомых. Начался дождь. Когда Эйнштейн собрался уходить, ему предложили взять шляпу.

– Зачем? – сказал Эйнштейн. – Я знал, что будет дождь, и именно поэтому не надел шляпу. Ведь она сохнет дольше, чем мои волосы.