Баллистика

Автор: – Движение тела в поле тяжести называют баллистическим. Ещё Галилей показал, что такое движение можно описать, разделив его на горизонтальную и вертикальную составляющие.

Задача 1.4. Пусть тело брошено под углом α к горизонту с начальной скоростью V₀. Требуется определить максимальную высоту Н подъема и дальность полета L.

Начнём с традиционного вопроса. Каков характер движения тела в горизонтальном и вертикальном направлениях? Силу трения о воздух можно не учитывать.

Студент: – На данное тело действует только сила тяжести. Поэтому, тело имеет ускорение g, направленное вниз. Горизонтальная составляющая скорости не меняется. Найдём начальные проекции скоростей:

V_0x = V₀cosα, V_0y = V₀sinα.

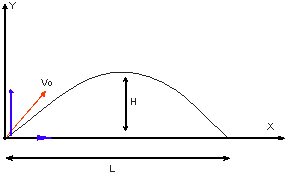
Рис. 1.3.1

Начнём с рассмотрения вертикальной составляющей движения. Полное время полета Т = Т ₁ + Т ₂, где Т ₁ – время подъема, Т ₂ – время спуска. Вертикальная скорость в наивысшей точке (в момент времени t = Т ₁) равна нулю. Применяя общую формулу для равнозамедленного движения, получим

V_y (t) = V₀sinα – gt.

Знак минус означает, что за положительное выбрано направление оси ОY. Для момента t = Т₁ имеем

0 = V₀sinα– gТ₁.

Отсюда

Т₁ = V₀ sinα/g.

Зная Т ₁, находим

Н = V_0yТ₁ – gТ₁²/2 = V₀sinαТ₁ – gТ₁²/2 = (V₀sinα)²/2g.

Время спуска найдём, рассмотрев падение тела с уже вычисленной высоты Н, но без начальной вертикальной скорости. Величина перемещения вдоль оси ординат в этом случае равна

Н = gТ₂²/2.

Значит,

Т₂ = 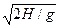= V₀ sinα/g.

Видим, что время спуска равно времени падения. А полное время в пути –

Т=2V₀sinα/g.

Рассмотрим горизонтальную составляющую движения. Как уже отмечалось, горизонтальное перемещение тела равномерное.

Х(t)=V₀cosα·t.

Отсюда находим

L = V₀cosαT = 2V₀cosαV₀sinα/g = V₀²sin2α/g. (1.7)

Автор: – Если нам необходимо попасть в цель, расположенную на оси ОХ на расстоянии L, то как надо стрелять?

Студент: – Угол прицела находится из (1.7)

sin2α = Lg/V₀².

Значит, стрелять надо под углом

α= 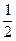arcsin(Lg/V₀²)

Кроме того, можно заметить, что максимальная дальность получается в случае, когда sin 2α=1, т. е. α=π/4.

Автор: – Это все верно, но пропущено ещё одно решение

β = (π/2) – α.

Стрелять можно двумя способами. Если угол прицела меньше 45^º, то говорят о настильной траектории, а если он больше 45^º, то такую траекторию называют навесной.

Студент: – А как можно установить вид траектории полета? В школе нам говорили, что она параболическая. Можно ли это обосновать?

Автор: – Для вывода уравнения траектории запишем зависимости координат Х и Y движущегося тела от времени:

Х = V₀cosαt; Y = V₀sinαt–gt²/2.

Исключая время с помощью первого выражения, получим:

Y = –gX²/(2V₀²cos²α) + Xtgα (1.8)

Это и есть уравнение параболы с ветвями, направленными вниз.

Студент: – Но для записи зависимости координаты Y от времени Вы использовали формулу для равнозамедленного движения. Однако во время спуска тело движется, ускоряясь.

Автор: Формула Y(t)= V₀sinαt–gt²/2 применима для любого момента времени, т. к. положительное направление оси ОY всегда противоположно вектору ускорения. Давайте убедимся в этом. Пусть Y ₀ – координата высшей точки траектории, обозначим τ какое-то время спуска. Тогда, за это время произошло следующее изменение ординаты тела:

Y₀ – Y = gτ²/2.

Так как

τ = t–T₁ = t– V₀sinα/g и

Y₀ = (V₀sinα)²/2g, то

(V₀sinα)²/2g–Y = (g/2)(t–V₀sinα/g)²

или окончательно

Y = V₀sinα∙t – gt²/2.

Теперь несколько усложним ситуацию.

Задача 1.5. На тело массой М, также брошенное под углом к горизонту, действует такой попутный горизонтальный ветер, что создает ускорение а. Найдите время полета Т, высоту Н и дальность L.

Студент: – По-моему, вертикальное движение совсем не изменилось, и можно воспользоваться некоторыми предыдущими результатами. Но в горизонтальном направлении тело испытывает ускорение а.

Автор: Правильно. Теперь догадайтесь, какие результаты предыдущей задачи можно использовать.

Студент: – ◄ Н = (V₀sinα)²/2g; Т = 2V₀sinα/g ►,

т. к. эти величины определяются только особенностями вертикального движения.

Автор: – Замечательно. Вам остается найти дальность полета.

Студент: – Зная горизонтальное ускорение и полное время полета, находим дальность:

◄ L = V₀cosα·T + aT²/2 = V₀²sin2α(1+ 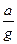tg α)/g ►.

Автор: – Это правильный ответ. И ещё одна дополнительная задача.

Задача №1.6.

Тело бросают под углом α к наклоненной плоскости, которая образует с горизонтом угол β. Начальная скорость – V₀. Найти расстояние L от точки бросания до точки падения тела.

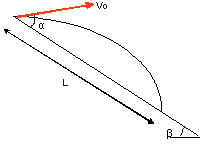
Рис. 1.3.2

Студент: – Мне кажется, что это сложная задача.

Автор: – Не торопитесь. Эта ситуация подобна предыдущей и легко сводится к ней. Действительно, выберём ось ОХ вдоль наклонной плоскости, а ось ОY перпендикулярно ей. Разложим векторы начальной скорости V₀ и ускорения свободного падения g на направления этих осей:

V_ox = V₀cosα, V_0y = V₀sinα, g_x = gsinβ, g_y = gcosβ.

Мы свели задачу к предыдущей. Но, в отличие от неё, здесь ускорение по оси ОХ вызывается не ветром, а составляющей силы тяжести gsinβ. Ускорение по оси ОY – силой gcosβ. Для определения L воспользуемся уже полученным результатом, сделав замену: a → gsinβ и g → gcosβ. Находим

◄ L = V₀² 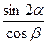(1 + tgα·tgβ)/g►.

При β = 0 этот результат совпадает с предыдущим ответом.

В заключение проведем исследование "границ поражения".

Задача 1.7. Как следует стрелять, допустим, из ружья, чтобы попасть в цель, находящуюся на расстоянии l по горизонтали и на высоте h?

Для начала ответьте, сколько может быть способов стрельбы?

Студент: – Мы уже встречались с ситуацией, когда мишень находилась на оси ОХ, и поняли, что возможны две траектории полета: настильная и навесная. Возможно, это распространяется и на другие случаи.

Автор: – Ваши качественные соображения верны. И ещё один предварительный вопрос. Если мишень расположена так, как определено условием задачи, то с какой минимальной скоростью можно стрелять, чтобы поразить мишень?

Студент: – На этот вопрос я могу ответить сразу. Стрелять надо так, чтобы наивысшая точка траектории пули совпала с координатами мишени (l, h). Получаем систему уравнений:

h = (V₀sinα)²/2g,

l = L/2 = V₀²sin2α/2g.

Разделив левые и правые части уравнений, получим:

h / l = 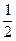∙tgα,

выразив sin ²α через значение tg α = 2 h/l, найдем начальную скорость.

Автор: – А почему Вы считаете, что из условия минимальности начальной скорости следует совпадение высшей точки траектории с положением мишени?

Студент: – Мне показалось, это очень естественно.

Автор: – К сожалению, Вы допустили ошибку, а Ваши чисто интуитивные соображения подвели. Поэтому будем считать "по-честному", не делая необоснованных предположений. Уравнение траектории Вам известно (1.8). Запишите условие выполнения этого соотношения для координат (l, h).

Студент: – Подставляю вместо Y значение h, а в качестве Х беру l. Получаю

h = –g l ²/(2V₀²cos²α) + l tgα.

Автор: – Здесь удобно выразить cos ²α через tg α, чтобы уравнение содержало только одну тригонометрическую функцию.

Студент: – 1 / cos²α = 1 + tg²α. Значит,

h = – (1 + tg²α)g l ² /(2V₀²) + (tgα)l.

Автор: – Вы правильно получили квадратное уравнение относительно tg α. Для удобства решения сделайте переобозначение и найдите корни.

Студент: Пусть tgα=Z, тогда уравнение примет вид:

g l²Z² /(2V₀²)– lZ + gl²/2V₀² + h = 0.

Умножим это уравнение на V₀²/l:

glZ²/2 – V₀²Z + gl/2 + hV₀²/l = 0

D = V₀⁴ –g(gl²+2V₀²h).

Если D > 0, то при данной начальной скорости пуля может попасть в цель двумя способами. При D < 0 пуля вообще не попадет в цель, т. е. ни одна из траекторий семейства (1.8) не достигает этой цели. Равенство дискриминанта нулю определяет ту минимальную начальную скорость, при которой ещё можно попасть в данную цель, т. к. D(V₀²) – монотонно возрастающая функция при V₀² > gh:

V²_min=g(h+ 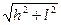) (1.9)

Для возможных углов выстрела получаем выражения

Z = 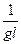(V₀² ± ):

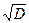Автор: – Найдите критический угол при минимально возможной скорости и сравните с Вашим прежним предположением.

Студент: – Z_кр= tgα_кр= V²_min /gl = 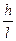+ 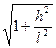. Это действительно отличается от того, что я писал раньше.

Автор: – Как бы Вы ответили на вопрос: может ли пуля попасть в цель с координатами (500 м, 500 м), если её начальная скорость 200 м/с?

Студент: – Я подставлю значения h =500 и l =500 в (1.9), если минимальная скорость получится меньше 200 м/с, то пуля попадет в мишень.

g(h + 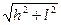)=10·(500+ 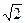·500)≈2,4·5000=12000; V≈110 м/с.

Вывод: скорость вполне достаточная, чтобы пуля попала в такую мишень.

Автор: – Верно. Можно написать уравнение границы поражения в общем виде. Выражая из (1.9) h и принимая начальную скорость V ₀, находим:

h= V₀² /(2g) – g l² /2 V₀² (1.10)

Эта формула определяет наибольшую высоту цели, находящейся на расстоянии l от ружья, в которую ещё можно попасть при данном значении V ₀. Поэтому на мой вопрос о попадании пули в конкретном случае можно ответить, подставив l и V ₀ в (1.10). Если получится значение, большее или равное 500 м, то пуля попадёт. В другом случае – нет. Проверьте свой вывод по этой формуле.

Студент: – 4·10⁴/20 – 25·10⁵ /8·10⁴ =2·10³ – 125/4>500. Вывод подтвердился.

История.

Нильс Бор с женой и молодым физиком Казимиром возвращались поздним вечером из гостей. Казимир был завзятым альпинистом и с удовольствием рассказывал о скалолазании, а затем предложил продемонстрировать свое мастерство, избрав для этого стену дома, мимо которого вся компания в тот момент проходила. Когда он, цепляясь за выступы, поднялся уже выше второго этажа, за ним, раззадорившись, двинулся Бор. Маргарита Бор с тревогой наблюдала за ними снизу. В это время послышались свистки, и к дому подбежало несколько полицейских. Здание оказалось отделением банка.