Движение по окружности

Автор: Важным частным случаем криволинейного движения является движение частицы по окружности. Положение тела будем характеризовать углом Δ α, образуемым двумя радиусами (рис. 1.4.1).

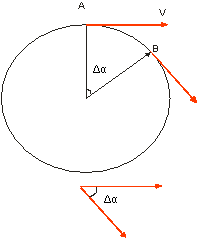
Рис. 1.4.1

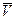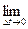На этом рисунке точками А и В обозначены соответственно начальное и конечное положения частицы. Наряду с линейной скоростью, которая определяется как и прежде (t)= Δ 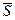(t)/Δt, удобно ввести угловую скорость ω, которая характеризует быстроту изменения угла α:

ω= 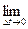Δα/Δt. (1.11)

Студент: – А куда направлена угловая скорость?

Автор: Это хороший вопрос, но не совсем простой. Вообще-то, угловая скорость, как и линейная, векторная величина. За её направление выбирают ось, перпендикулярную плоскости вращения частицы, т. е. плоскости рис. 1.4.1. При этом условно договорились, что, если частица вращается против часовой стрелки, то угловая скорость направлена на нас. А если по часовой, – то от нас, вглубь рисунка. Знак угловой скорости зависит от направления вращения.

Но во всех задачах, которые мы будем рассматривать, нас будут интересовать только знаки угловых скоростей и абсолютные величины угловых скоростей.

Найдем взаимосвязь между модулями линейной и угловой скоростей. Длина дуги L, стягивающая угол α, равна L= αR, где R – радиус окружности, а угол α измерен в радианах. Поэтому

ΔL=RΔα.

Отсюда, разделив обе части уравнения на Δt, получаем

V= ωR (1.12)

Удобно использовать период обращения Т – это время полного оборота. А также определим частоту ν – величину, обратную периоду Т, которая определяет число оборотов за единицу времени:

ν =1/Т.

Видим, что

Т=2πR/V=2π/ω; ν= ω/2π. (1.12a)

Студент: – Если честно, то я не очень понял, почему дробь 1/Т дает число оборотов в единицу времени.

Автор: – Поясню на примере. Пусть за 1 секунду частица совершила 10 оборотов. Чему равен период Т?

Студент: – Кажется, я догадался: Т =1/10, отсюда по определению получаем ν =10, что совпадает с условием.

Автор: – И последнее понятие: угловое ускорение. Вводится по аналогии с линейным:

ε= 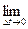Δω/Δt (1.13)

Следует пояснить, что, строго говоря, ε – векторная величина, и если движение происходит в одной плоскости, то вектор ε направлен перпендикулярно плоскости вращения. Но мы ограничимся только расчетом абсолютной величины ε.

При движении тела по окружности с постоянной по величине скоростью говорят, что оно совершает равномерное вращение.

Пусть в момент времени t тело находится в точке А окружности, а в момент t+Δt – в точке В. Длина дуги АВ равна Δs=RΔα, где R – радиус окружности, а Δα – угловое смещение за промежуток времени Δt. Обозначая модуль скорости V, получим Δs= VΔt, откуда Δt=RΔα/V.

Перенесем вектор V(t+ Δt) из точки В в точку А и рассмотрим получившийся векторный треугольник. Он равнобедренный, угол при вершине равен Δα (поскольку стороны этого угла перпендикулярны сторонам 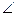АОВ). Длина основания треугольника равна

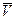| (t+ Δt)– 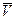(t)|=2Vsin(Δα/2).

Для дальнейших преобразований нам понадобится одно математическое свойство:

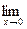
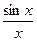=1.

Находим искомое выражение модуля ускорения:

а= 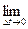| 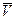(t+ Δt)– 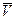(t)|/Δt= 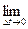[2Vsin(Δα/2):(RΔα/V)]=

=(V²/R)∙ 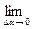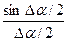= V²/R.

Направлено это ускорение в центр О, поэтому его называют центростремительным. Запишем результат для а _ц.с. двумя способами:

а_ц.с =V²/R=ω²R (1.14)

Подведите итог самостоятельно.

Студент: – При равномерном вращении по окружности, вектор ускорения ориентирован по радиусу к центру окружности. При вращении вектор центростремительного ускорения меняется, но модуль его неизменен и равен

а_ц.с =V²/R=ω²R.

Вектор скорости в каждой точке траектории направлен по касательной к окружности и также не меняется по модулю, V= ωR.

А как изменится ситуация при неравномерном вращении по окружности?

Автор: – В этом случае скорость меняется как по направлению, так и по модулю. То же можно сказать и про ускорение. Вектор ускорения удобно представить в виде суммы ортогональных векторов:

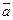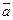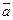= _ц.с + _τ.

Здесь: 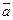_ц.с – центростремительное ускорение, оно связано с изменением скорости частицы по направлению; 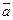_τ – тангенциальное ускорение, связанное с изменением модуля скорости; 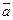_ц.с направлено по радиусу к центру, а ускорение 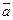_τ - по касательной к окружности.

Рассмотрите, для примера, ситуацию, когда тело неравномерно движется по окружности c радиусом R. Линейная скорость изменяется по закону V(t)=a₀t. Необходимо найти ускорение в момент t.

Студент: – Центростремительное ускорение определю из (1.14)

а_ц.с =V²/R= (a₀t)²/R.

Тангенциальное ускорение можно найти так:

а_τ= [a₀ (t+ Δt)– a₀ t]/Δt = a₀ Δt/Δt= a_0.

Автор: – Правильно. Добавим только, что полное ускорение найдем по теореме Пифагора:

а=(а_ц.с² + а_τ²)^1/2= a₀(а₀²t⁴/R² + 1) ^1/2 .

История.

Вольфганг Паули был 100-процентным теоретиком. Его неспособность обращаться с любым оборудованием вошла у друзей в поговорку. Утверждали, что ему достаточно просто войти в лабораторию, чтобы в ней что-нибудь сразу же переставало работать. Это мистическое явление окрестили «эффектом Паули» (в отличие от знаменитого «принципа Паули»). Из документально зарегистрированных проявлений эффекта Паули самым поразительным является следующий. Однажды в лаборатории Джеймса Франка в Геттингене произошел настоящий взрыв, разрушивший дорогую установку. Время этого ЧП было достаточно точно зафиксировано. Как потом оказалось, взрыв произошел именно в тот момент, когда поезд, в котором Паули следовал из Цюриха в Копенгаген, остановился на 8 минут в Геттингене.