Дифференциальные уравнения в частных производных
Методические указания по теме 1.3:
Дифференциальные уравнения в частных производных:
Пусть искомая функция 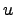 зависит от нескольких независимых переменных
зависит от нескольких независимых переменных 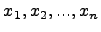
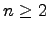
Уравнение, связывающее искомую функцию, независимые переменные и частные производные от искомой функции, называется дифференциальным уравнением с частными производными. Оно имеет вид:
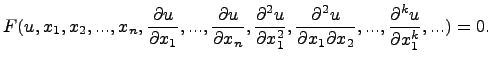
Здесь 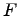 -- данная функция своих аргументов. Порядок старшей частной производной, входящей в уравнение, называется порядком уравнения частными производными.
-- данная функция своих аргументов. Порядок старшей частной производной, входящей в уравнение, называется порядком уравнения частными производными.
Дифференциальное уравнение с частными производными первого порядка с 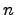 независимыми переменными может быть записано в форме:
независимыми переменными может быть записано в форме:
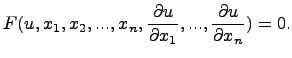
Общее решение дифференциального уравнения с частными производными, вообще говоря, может зависеть от некоторых произвольных (гладких) функций.
Пример 1. Рассмотрим уравнение в частных производных второго порядка
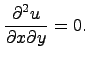
Написав его в виде 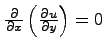 , убеждаемся в том, что
, убеждаемся в том, что 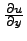 не зависит от
не зависит от 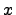 . Мы можем положить его равным произвольной функции от
. Мы можем положить его равным произвольной функции от 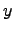 :
: 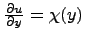 . Интегрируем последнее равенство по
. Интегрируем последнее равенство по 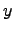 . Замечая, что постоянная интеграции есть постоянная по отношению к
. Замечая, что постоянная интеграции есть постоянная по отношению к 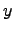 , т.е. может быть любой функцией от
, т.е. может быть любой функцией от 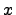 , и что
, и что 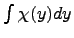 -- опять произвольная (дифференцируемая) функция от
-- опять произвольная (дифференцируемая) функция от 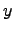 , получаем общее решение данного уравнения:
, получаем общее решение данного уравнения:
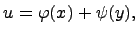
где 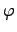 ,
, 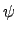 -- произвольные функции, которые, конечно, должны быть дифференцируемы, чтобы имел смысл результат подстановки в данное уравнение. В этом случае общее решение уравнения зависит от двух произвольных функций.
-- произвольные функции, которые, конечно, должны быть дифференцируемы, чтобы имел смысл результат подстановки в данное уравнение. В этом случае общее решение уравнения зависит от двух произвольных функций.
Для уравнений в частных производных можно вводить различные добавочные данные, которые определяют при некоторых условиях однозначно частное решение. В частности, можно использовать начальные данные Коши. Для одного уравнения 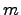 -ого порядка, разрешенного относительно одной из старших производных, вида
-ого порядка, разрешенного относительно одной из старших производных, вида
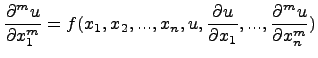
начальные условия при 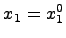 имеют вид
имеют вид
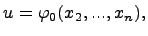
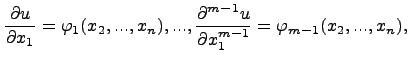
где 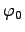 ,
, 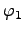 ,...,
,..., 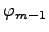 -- заданные функции. Нахождение решения уравнения, удовлетворяющего указанным условиям, есть задача Коши.
-- заданные функции. Нахождение решения уравнения, удовлетворяющего указанным условиям, есть задача Коши.
В общем случае уравнение в частных производных может не иметь общего решения, зависящего от конечного набора функций или постоянных параметров. Уравнения в частных производных первого порядка обладают общим решением, зависящим от одной произвольной функции. Задача интегрирования уравнения в частных производных первого порядка сводится к интегрированию системы обыкновенных дифференциальных уравнений.
Рассмотрим линейное однородное уравнение в частных производных:
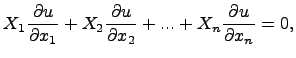
где 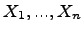 -- данные функции независимых переменных
-- данные функции независимых переменных 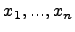 , непрерывные и непрерывно дифференцируемые в рассматриваемой области. Наряду с дифференциальным уравнением в частных производных напишем систему обыкновенных дифференциальных уравнений:
, непрерывные и непрерывно дифференцируемые в рассматриваемой области. Наряду с дифференциальным уравнением в частных производных напишем систему обыкновенных дифференциальных уравнений:
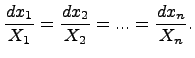
Левая часть любого первого интеграла системы обыкновенных дифференциальных уравнений есть решение уравнения в частных производных. И обратно, всякое решение уравнения в частных производных, приравненное произвольной постоянной, дает первый интеграл выписанной системы обыкновенных дифференциальных уравнений. Пусть
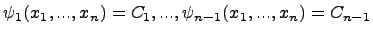
есть некоторая определенная система независимых интегралов составленной системы обыкновенных дифференциальных уравнений. Тогда для произвольной дифференцируемой функции 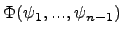 суперпозиция функций
суперпозиция функций 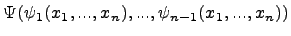 является общим решением линейного однородного уравнения в частных производных.
является общим решением линейного однородного уравнения в частных производных.
Для уравнения
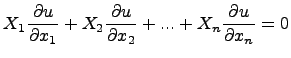
решим задачу Коши с начальными данными:
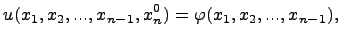
где 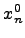 -- заданное число,
-- заданное число, 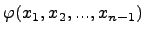 -- заданная дифференцируемая функция своих аргументов. Пусть
-- заданная дифференцируемая функция своих аргументов. Пусть  -- независимые первые интегралы. Пусть далее
-- независимые первые интегралы. Пусть далее 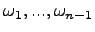 -- такие функции, что
-- такие функции, что
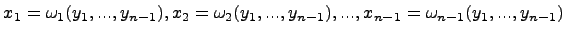
являются решениями системы уравнений
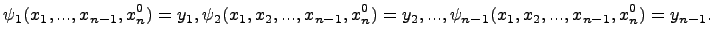
Тогда искомое частное решение дифференциального уравнения в частных производных имеет вид
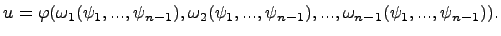
Вопросы для самопроверки по теме 1.3:
Уравнение, какого вида называется дифференциальным уравнением в частных производных?
 2015-10-16
2015-10-16 1966
1966
