Задачи, приводящие к дифференциальным уравнениям:
В различных областях науки и техники весьма часто встречаются задачи, для решения которых требуется решить одно или несколько уравнений, содержащих производные некоторых функций. Такие уравнения называются дифференциальными.
Пример 1. На плоскости хОу требуется найти кривую, проходящую через точку О (0; 0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания.
Пусть y = f (x) — уравнение искомой кривой. По условию, в каждой точке М (х; f (х)) имеется касательная к этой кривой, угловой коэффициент которой, т. е. f ' (x), равен 2 х. Таким образом, 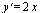 (1) Это дифференциальное уравнение, так как оно содержит производную искомой функции. Из уравнения (1) следует, что функция у есть первообразная функции 2 х. Поэтому
(1) Это дифференциальное уравнение, так как оно содержит производную искомой функции. Из уравнения (1) следует, что функция у есть первообразная функции 2 х. Поэтому 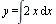 или
или 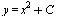 , (2)где С — произвольная постоянная. Из формулы (2) видно, что дифференциальное уравнение (1) имеет бесконечное множество решений. Чтобы из этого множества решений выбрать искомое, надо воспользоваться тем, что искомая кривая проходит через точку О (0; 0). Следовательно, координаты этой точки должны удовлетворять уравнению (2), т. е. 0 = 0 + С, откуда С = 0. Итак, искомая кривая — это парабола
, (2)где С — произвольная постоянная. Из формулы (2) видно, что дифференциальное уравнение (1) имеет бесконечное множество решений. Чтобы из этого множества решений выбрать искомое, надо воспользоваться тем, что искомая кривая проходит через точку О (0; 0). Следовательно, координаты этой точки должны удовлетворять уравнению (2), т. е. 0 = 0 + С, откуда С = 0. Итак, искомая кривая — это парабола 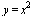 .
.
Пример 2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю.
В этом случае, как известно, скорость выражается формулой 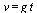 Так как скорость прямолинейного движения есть производная пути по времени, то
Так как скорость прямолинейного движения есть производная пути по времени, то 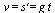 (3) Из этого уравнения следует, что функция s есть первообразная функции g t. Поэтому
(3) Из этого уравнения следует, что функция s есть первообразная функции g t. Поэтому 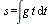 или
или 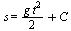 (4) Для нахождения произвольной постоянной С воспользуемся тем, что начало отсчета пути совпадает с началом отсчета времени, т. е. s = 0 при t = 0. Подставляя эти значения в равенство (4), имеем 0 = 0 + С, откуда С = 0 и, следовательно,
(4) Для нахождения произвольной постоянной С воспользуемся тем, что начало отсчета пути совпадает с началом отсчета времени, т. е. s = 0 при t = 0. Подставляя эти значения в равенство (4), имеем 0 = 0 + С, откуда С = 0 и, следовательно,
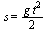 .
.
Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения:
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производное или дифференциалы.
Символически дифференциальное уравнение записывается так: 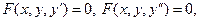
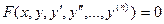 .
.
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значимых произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента или функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнениям первого порядка называются уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называются уравнения вида
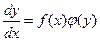
Для решения этого уравнения нужно сначала разделить переменные:
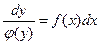 , а затем проинтегрировать обе части полученного равенства:
, а затем проинтегрировать обе части полученного равенства:
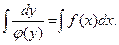
Пример 3. Найдите общее решение уравнений с разделяющимися переменными.
а) 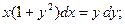
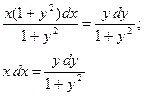
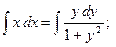
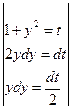 ;
;
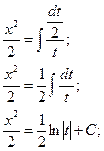
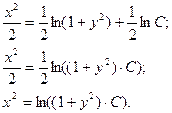
б) 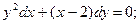
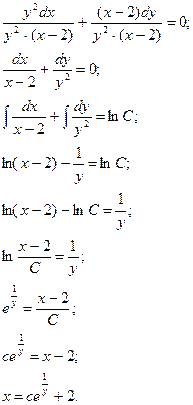
Однородные дифференциальные уравнения первого порядка:
Уравнения вида 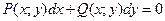 называется однородным, если
называется однородным, если 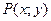 и
и 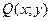 -однородные функции одного измерения.
-однородные функции одного измерения.
Функция 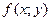 называется однородной измерения m, если
называется однородной измерения m, если 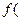 и
и 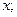 и
и 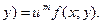
С помощью подстановки 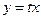 однородное уравнение приводится к уравнению с разделяющимися переменными.
однородное уравнение приводится к уравнению с разделяющимися переменными.
Пример 4. Решите однородное дифференциальное уравнение первого порядка.
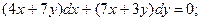
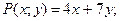
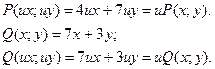
Замена: 
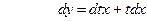
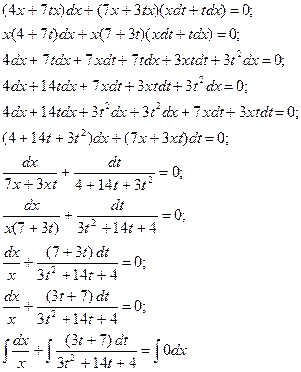
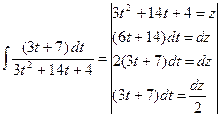 =
= 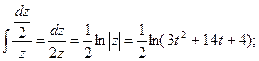
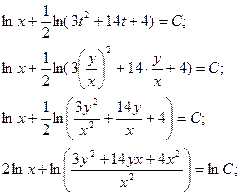
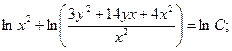
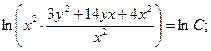
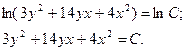
Уравнение вида 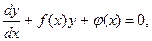 где
где 
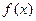 и
и 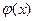 - функции от х, называется линейным дифференциальным уравнением первого порядка. В частном случае
- функции от х, называется линейным дифференциальным уравнением первого порядка. В частном случае 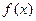 и
и 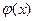 могут быть постоянными величинами.
могут быть постоянными величинами.
Это уравнение приводит к уравнению с разделяющимися переменными с помощью подстановки 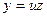 , где и
, где и 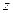 - новые функции от
- новые функции от 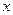 .
.
Пример 5. Решите линейное дифференциальное уравнение первого порядка.
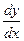 -
- 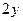 - 3 =0;
- 3 =0;
Положим 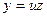 . Продифференцируем по
. Продифференцируем по 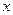 :
: 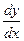 =
= 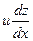 +
+ 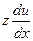 .
.
Подставим эти выражения в уравнения, получим:
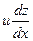 +
+ 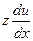 -
- 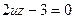 ;
;
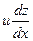 +
+ 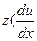 -
- 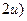 -3=0; (*)
-3=0; (*)
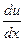 -
- 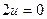 ;
;
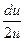 -
- 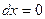 ;
;
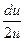 =
= 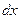 ;
;
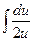 =
= 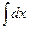 ;
;
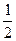
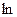
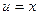 ;
;
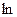
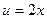 ;
;
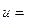
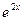 ;
;
Подставим теперь выражение для 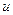 в уравнение (*), тогда получим уравнение
в уравнение (*), тогда получим уравнение
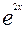
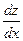 -3=0;
-3=0;
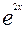
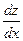 =3;
=3;
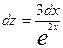 ;
;
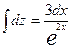 ;
;
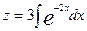 ;
;
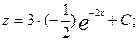 ;
;
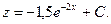 .
.
Зная 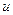 и
и 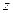 , теперь получаем общее решение данного уравнения:
, теперь получаем общее решение данного уравнения:
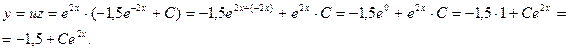
Пример 6. Найдите частные решения дифференциального уравнения:
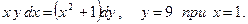
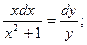
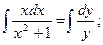
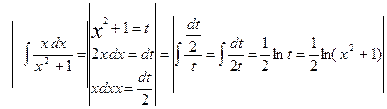
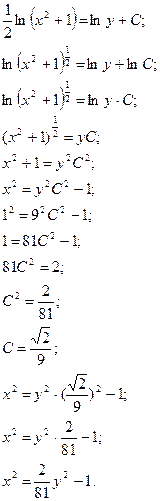
Линейные однородные уравнения второго порядка с постоянными коэффициентами:
Уравнение, содержащие производные (или дифференциалы) не выше второго порядка, называется дифференцированным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом: 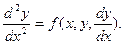
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.
Пример 7. Найдите частное решение уравнения, удовлетворяющее указанным начальным условием 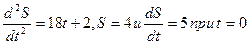
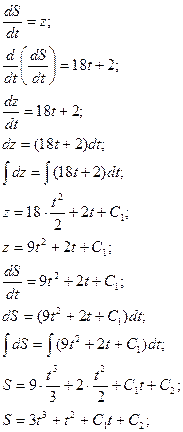
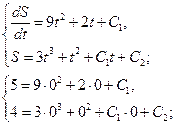
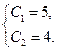
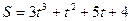
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
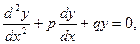 (1)
(1)
где p и q – постоянные величины.
Для отыскания общего решения уравнения (1) заменой 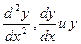 на соответствующие степени
на соответствующие степени 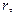 причем сама функция
причем сама функция 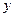 заменяется единицей. Тогда общее решение дифференциального уравнения (1) строится в зависимости от корней
заменяется единицей. Тогда общее решение дифференциального уравнения (1) строится в зависимости от корней 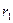 и
и 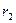 характеристического уравнения (2). Здесь возможны три случая.
характеристического уравнения (2). Здесь возможны три случая.
I случай. Корни 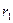 и
и 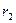 - действительны и различные. В этом случае общее решение уравнения (1) имеет вид:
- действительны и различные. В этом случае общее решение уравнения (1) имеет вид:
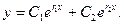 (3)
(3)
II случай. Корни 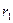 и
и 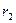 - действительные и равные:
- действительные и равные: 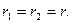 Тогда общее решение уравнение (1) записывается так:
Тогда общее решение уравнение (1) записывается так:
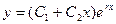 (4)
(4)
III случай. Корни 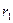 и
и 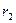 - комплексно-сопряженные:
- комплексно-сопряженные: 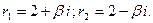 В этом случае общее решение уравнения (1) записывается следующим образом:
В этом случае общее решение уравнения (1) записывается следующим образом:
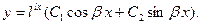 (5)
(5)
Пример 8. Найдите частные решения дифференциальных уравнений.
а) 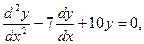 при
при 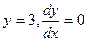 при
при 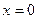 .
.
Составим характеристическое уравнение и найдите его корни.
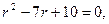
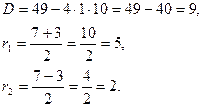
Так как корни характеристического уравнения действительны и различны, то общее решение данного дифференциального уравнения согласно формуле (3) запишется так:
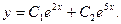
Для нахождения искомого частного решения нужно определить значения постоянных С1 и С2. Подставив в общее решение значения 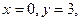 получим:
получим:
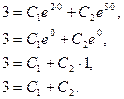
Продифференцировав общее решение и подставив в полученное выражение 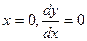 , имеем:
, имеем:
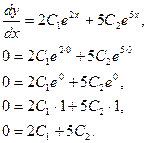

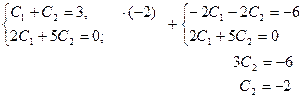

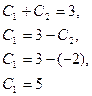
Таким образом, искомое частное решение имеет вид
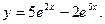
Вопросы для самопроверки по теме 1.2:
1. Что называется дифференциальным уравнением?
2. Что называется решением дифференциального уравнения?
3. Что называется частными решениями дифференциального уравнения?
4. Какой вид имеет дифференциальное уравнение с разделяющимися переменными?
5. Какой вид имеет однородное дифференциальное уравнение?
6. Какой вид имеет линейное дифференциальное уравнение первого порядка.
7. Какое уравнение называется дифференциальным уравнением второго порядка?
8. Какой общий вид уравнения второго порядка?
9. Какой общий вид линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами?
Задания для самостоятельного решения по теме 1.2:
1.Найти общее решение уравнения: 1) 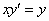 ;
;
2) 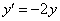 ;
;
3) 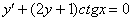
2.Найдите общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям:
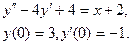
3.Найдите общее решение дифференциального уравнения: 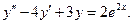
 2015-10-16
2015-10-16 1116
1116








