Вычисление пределов функций с использованием первого и второго замечательных пределов:
Краткие теоретические сведения по теории пределов:
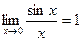 - 1-й замечательный предел.
- 1-й замечательный предел.
Следствия:
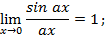
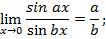
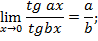
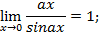
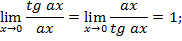
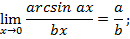
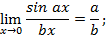
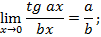
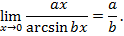
Пример 1. Вычислить предел:
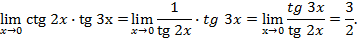
Пример 2. Вычислить предел:
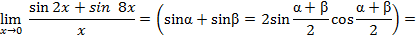
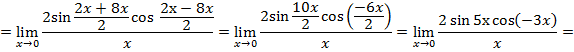
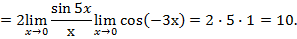
Пример 3. Вычислить предел:
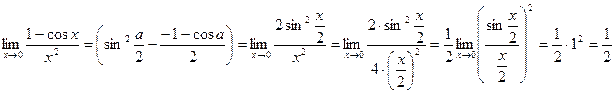
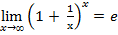 – 2-й замечательный предел.
– 2-й замечательный предел.
Следствие 1.
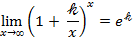
Следствие 2.
Сделаем замену:  = y => x =
= y => x =  .
.
Тогда при x→∞ y→0 и 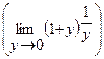
Пример 4. Вычислить предел:
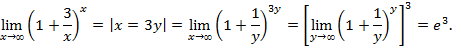
Пример 5. Вычислить предел:

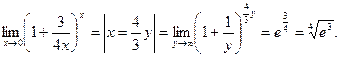
Пример 5. Вычислить предел:
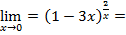
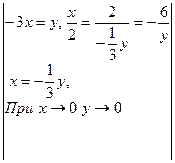 =
= 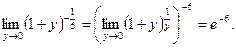
Пример 6. Вычислить предел:
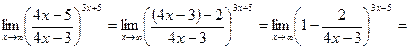
= 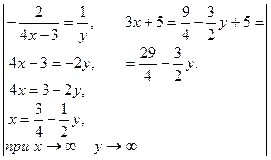 =
=
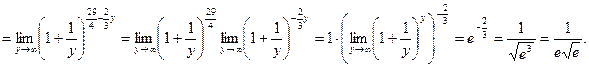
Две бесконечно малые величины 𝛂(x) называются эквивалентными (или равносильными) при x → a, если 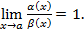
Таблица эквивалентных величин (всюду x→0)
sin 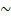 x
x
arcsin x 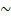 x
x
tg x 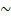 x
x
arctg x 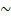 x
x
ex-1 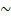 x
x
ln( 1+ x) 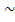 x
x
ax 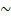 x ln a, a≠1, a>0
x ln a, a≠1, a>0
loga(1+x) 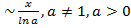
(1+x)𝛂 -1 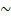 𝛂x, 𝛂
𝛂x, 𝛂 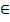 R
R
1-cos x 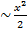
Пример 7. Найти предел:
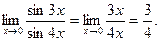
Пример 8. Найти предел:
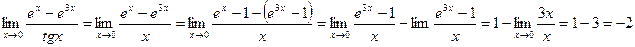
Исследование функций на непрерывность:
Если в какой либо точке х0 функция 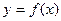 не является непрерывной, т.е.
не является непрерывной, т.е. 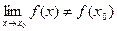 , то точка
, то точка 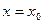 называется точкой разрыва этой функции, а функция
называется точкой разрыва этой функции, а функция 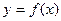 называется разрывной в этой точке.
называется разрывной в этой точке.
Пусть аргумент 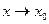 остается все время слева от
остается все время слева от 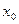 , т.е.
, т.е. 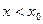 . Если при этом условии функция
. Если при этом условии функция 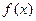 имеет предел – число
имеет предел – число 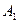 , то это число называется односторонним пределом функции слева в точке
, то это число называется односторонним пределом функции слева в точке 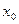 обозначается:
обозначается: 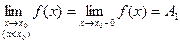 .
.
Односторонний предел справа:
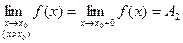
Пример 8. Вычислить односторонние пределы:
а) 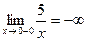 ;
;
б) 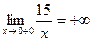 ;
;
в) 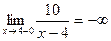 ;
;
г) 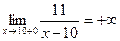 ;
;
д) 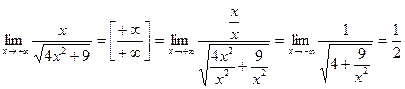 ;
;
е) 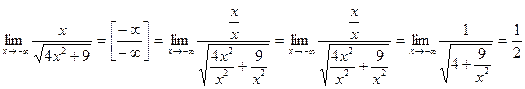 .
.
Функция 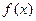 называется непрерывной в точке
называется непрерывной в точке 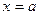 , если предел функции при
, если предел функции при 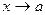 равен значению функции при
равен значению функции при 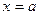 , т.е.
, т.е. 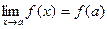 .
.
Если условие непрерывности функции в точке 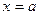 нарушено, то такую точку называют точкой разрыва функции.
нарушено, то такую точку называют точкой разрыва функции.
Точка 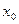 является точкой разрыва первого рода функции
является точкой разрыва первого рода функции 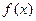 , если в этой точке функция
, если в этой точке функция 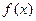 имеет конечные, но не равные друг другу левый и правый пределы:
имеет конечные, но не равные друг другу левый и правый пределы: 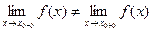 .
.
Точка x0 является разрывом второго рода функции 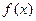 , если в этой точке не существует хотя бы одного из односторонних пределов функции
, если в этой точке не существует хотя бы одного из односторонних пределов функции 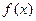 или хотя бы один из односторонних пределов бесконечен.
или хотя бы один из односторонних пределов бесконечен.
Пример 9. Установить характер точки разрыва функции в точке или доказать непрерывность функций:
а) 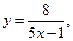
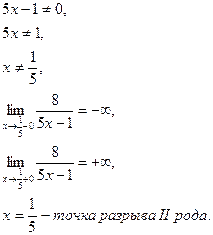
б) 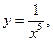
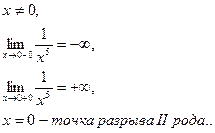
в) 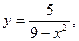
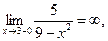
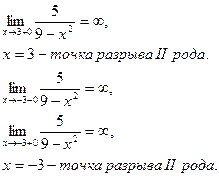
г) 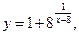
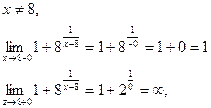
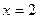 точка разрыва II рода.
точка разрыва II рода.
д) 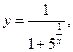
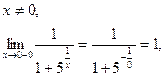
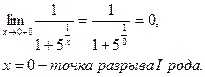
Нахождение производных по алгоритму:
Производной функции y=f (x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
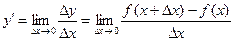 .
.
Производная функции имеет несколько обозначений: y′, f′(x), 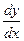 ,
, 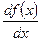 .
.
Нахождение производной функции называется дифференцированием этой функции.
Таблица производных:
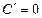 ,
, 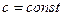 ;
; 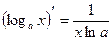 ;
;
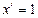 ;
; 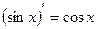 ;
;
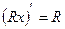 ;
; 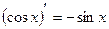 ;
;
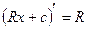 ;
; 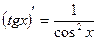 ;
;
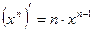 ;
; 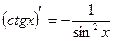 ;
;
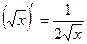 ;
; 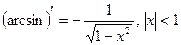 ;
;
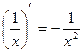 ;
; 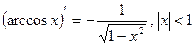 ;
;
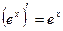 ;
; 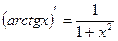 ;
;
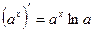 ;
; 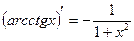 .
.
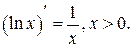
Правила вычисления производных.
1. 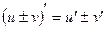 .
.
2. 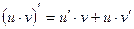 ;
;
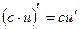 ;
;
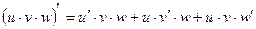 .
.
3. 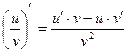 .
.
Пример 10. Найти производные функции:
1) 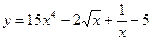
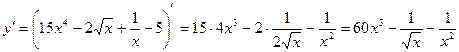 ;
;
2) 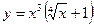
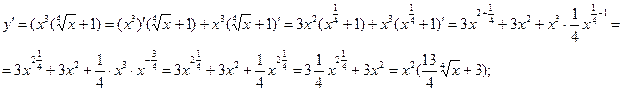 3)
3) 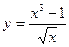
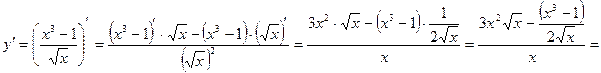
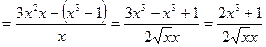 .
.
Вычисление производных сложных функций:
Если y=f (u) и 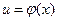 – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного аргумента и по независимой переменной x, т.е.
– дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного аргумента и по независимой переменной x, т.е. 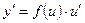 .
.
С учетом полученного правила дифференцирования сложной функции для функции y=un, где u=u(f), можно записать:
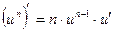 ,
,
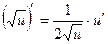 ′,
′,
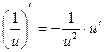 .
.
Пример 11. Найти производные функций:
1) 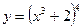
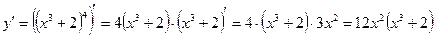 ;
;
2) 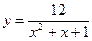
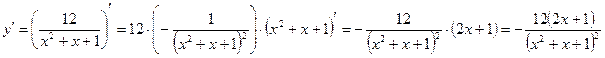 ;
;
3) 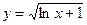 ;
;
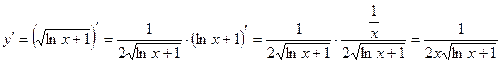 ;
;
4) 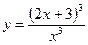
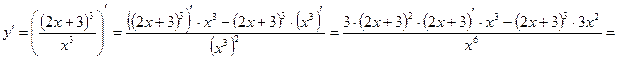
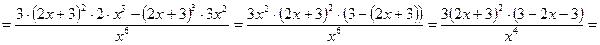
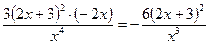 ;
;
5) 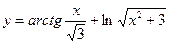
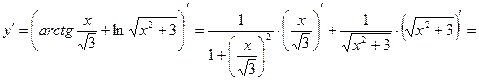
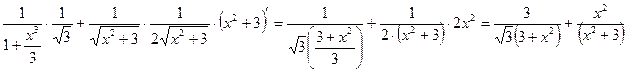
Общая схема построения графиков функций:
- Область определения функции.
- Четность, периодичность функции.
- Точки пересечения графика с осями координат (если это не вызывает затруднений).
- Асимптоты графика функции.
- Промежутки монотонности функции и экстремумы.
- Промежутки выпуклости графика функции и точки перегиба.
- Дополнительные точки (если возможно)
8. График функции.
Пример 12. Исследовать функцию у=х3-5х2+3х-5 построить график:
- D(у)=(-∞; ∞)
- у(-х)=(-х)3-5
 (-х)2+3
(-х)2+3  (-х)-5 = -х3-5х2-3х-5≠у(х) ≠-у(х).
(-х)-5 = -х3-5х2-3х-5≠у(х) ≠-у(х).
Функция не является ни чётной ни нечётной.
3. Точка пересечения с осью у:
x=0, у=03-5  02+3
02+3  0-5=-5
0-5=-5
(0;-5) – точка пересечения с осью у.
Точки пересечения с осью х найти затруднительно.
4. Вертикальных асимптот нет, т.к. функция непрерывна на (-∞;∞).
Наклонная асимптота: у=kх+b.
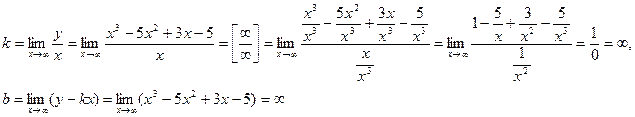 Наклонных асимптот нет.
Наклонных асимптот нет.
5. у/=(х3-5х2+3х-5)/=3х2-10х+3;
у/=0; 3х2-10х+3=0,
D=100-4  3
3  3=100-36=64,
3=100-36=64,
x1= 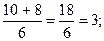
x 2= 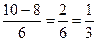 .
.
x1=3; х2 = 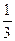 -критические точки функции.
-критические точки функции.
| x | (- 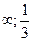 ) ) | 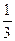 |  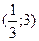 | 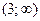 | |
| у/ | + | - | + | ||
| у |  | 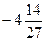 |  | -14 |  |
| max | min |
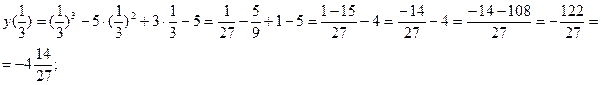
y (3)=33-5  32+3
32+3  3-5=27- 45+9-5= -14
3-5=27- 45+9-5= -14
(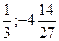 ) – точка max; (3;-14) – точка min
) – точка max; (3;-14) – точка min
- у//=(3х2-10х+3)/=6х-10
у//=0; 6х-10=0,
6х=10,
x= 1 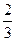 .
.
| х | 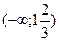 | 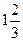 | 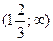 |
| у// | - | 0 |  + + |
| у |  | 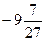 | |
| точка перегиба |
у(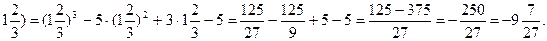
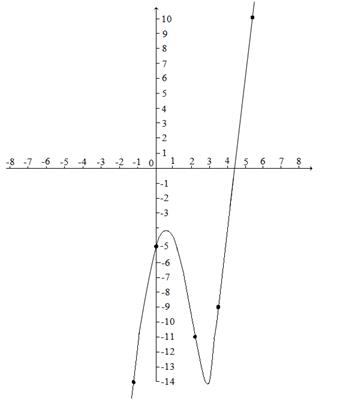
|
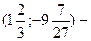 точка перегиба
точка перегиба | x | y |
| -1 | -14 |
| -11 | |
| -9 | |
|
Пример 13.Исследовать функцию F(x)= 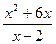 и построить её график.
и построить её график.
1) х-2≠0,
х≠2,
D(f)=(-∞;2) 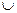 (2;∞)
(2;∞)
2)f(-х)= 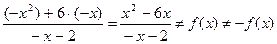 функция не является ни чётной, ни нечетной.
функция не является ни чётной, ни нечетной.
Функция не периодическая.
3) точка пересечения с осью Оу:
x=0; у=0
(0;0) – точка пересечения с осью Оу. Точки пересечения с осью Ох.
y =0, 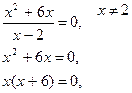
x =0 или х+6=0,
x =-6.
(0;0), (0;-6) – точки пересечения с осью Ох.
4) х =2 – точка разрыва II рода.
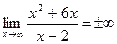
x=2 – вертикальная асимптота.
y= kx+b – наклонная асимптота.
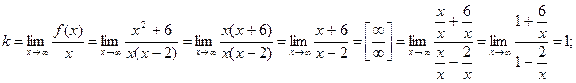
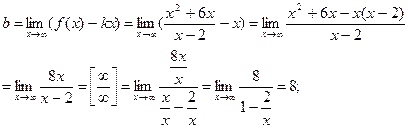
y=1  х+8;
х+8;
y= х+8 - наклонная асимптота.
5) 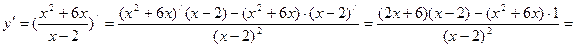
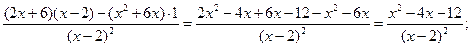
у/=0 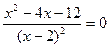 , х≠2
, х≠2
х2-4х-12=0
D=16-4  1
1  (-12)=16+48=64
(-12)=16+48=64
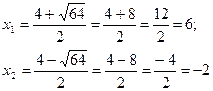
x1=6; х2=-2 – критические точки
| х | (-∞;-2) | -2 | (-2;2) | 2 | (2;6) | 6 | (6; ∞) |
| у/ | + | 0 | - | - | 0 | + | |
| у |  | 2 |  |  | 18 |  | |
| max | точка разрыва | min |
y( -2)= 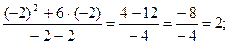
y( 6)= 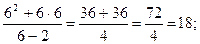
(-2;2) – точка max
(6;18) – точка min
6) у//= 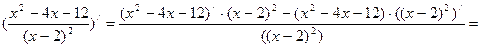
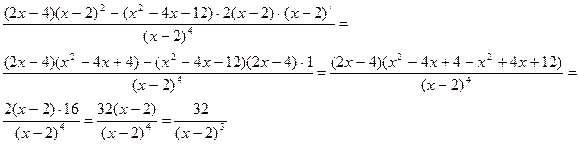
у//=0; 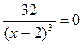 х≠2.
х≠2.
32≠0
нет критических точек II рода.
| х | (-∞;2) | 2 | (2; ∞) |
| у// | - |  + + | |
| у |  | ||
| точка разрыва |
 7) дополнительные точки
7) дополнительные точки
 х у
х у
4 20
10 20
Функции нескольких переменных:
Переменная величина 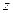 называется функцией двух переменных величин
называется функцией двух переменных величин 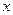 и
и 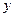 , если каждой паре допустимых значений
, если каждой паре допустимых значений 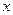 и
и 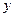 соответствует единственное значение
соответствует единственное значение 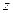 .
.
Функции двух переменных обозначают символами 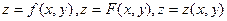 и т.п.
и т.п.
Значение функции 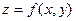 при
при 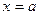 и
и 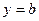 обозначают через
обозначают через 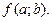
Упорядоченная пара значений 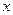 и
и 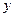 называется точкой М
называется точкой М 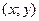 , а функция двух переменных – функцией этой точки
, а функция двух переменных – функцией этой точки 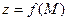 .
.
Переменная величина и называется функцией трех переменных величин 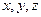 , если каждой упорядоченной тройке значений
, если каждой упорядоченной тройке значений 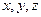 соответствует единственное значение и.
соответствует единственное значение и.
Аналогично определяется функция 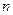 переменных.
переменных.
Нахождение частных производных:
Частной производной функции 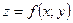 по переменной x называется производная этой функции при постоянном значении переменной y; она обозначается
по переменной x называется производная этой функции при постоянном значении переменной y; она обозначается 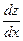 или
или 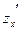 .
.
Частной производной функции 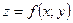 по переменной y при постоянном значении переменной x; она обозначается
по переменной y при постоянном значении переменной x; она обозначается 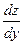 или
или 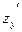 .
.
Частная производная функции нескольких переменных по одной переменной определяется как производная этой функции по соответствующей переменной при условии, что остальные переменные считаются постоянными.
Полным дифференциалом функции 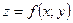 в некоторой точке М(x;y) называется выражение
в некоторой точке М(x;y) называется выражение 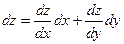 , где
, где 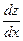 и
и 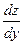 вычисляются в точке M(x;y), а
вычисляются в точке M(x;y), а
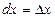 ,
, 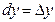 .
.
Пример 14. Найдите частные производные функции:
а) 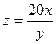 ;
;
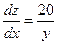 ;
;
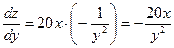 ;
;
б) 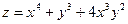 ;
;
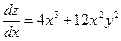 ;
;
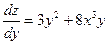 ;
;
в) 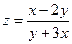 ;
;
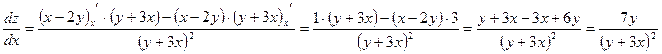
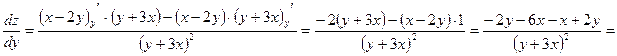
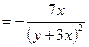
г) 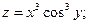
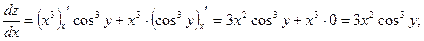
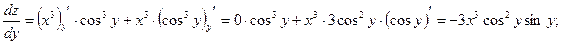
д) 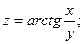
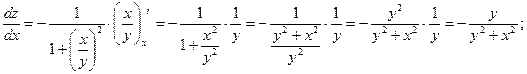
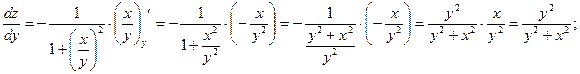
е) 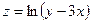 ;
;
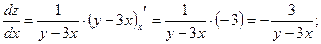
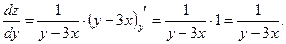
Неопределенный интеграл. Непосредственное интегрирование:
Таблица интегралов.
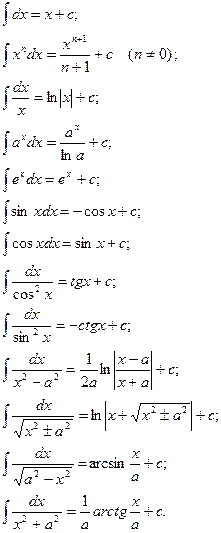
Замена переменной:
Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла 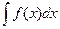 в интеграл
в интеграл 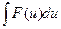 , который легко вычисляется по какой либо из основных формул интегрирования.
, который легко вычисляется по какой либо из основных формул интегрирования.
Для нахождения интеграла 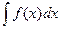 заменяем переменную
заменяем переменную 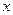 новой переменной
новой переменной 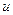 с помощью подстановки
с помощью подстановки 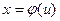 .
.
Дифференцируя это равенство, получим 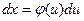 . Подставляя в подынтегральное выражение вместо
. Подставляя в подынтегральное выражение вместо 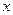 и
и 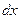 их значения выраженные через
их значения выраженные через 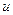 и
и 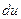 , имеем:
, имеем:
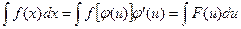 .
.
После того как интеграл относительно новый переменной и будет найден с помощью подстановки 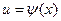 он приводится к переменной
он приводится к переменной 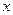 .
.
Пример 15. Найти следующие интегралы:
1) 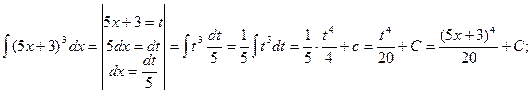
2) 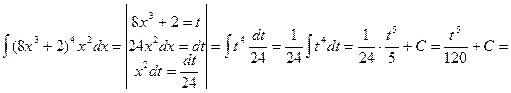
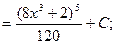
3) 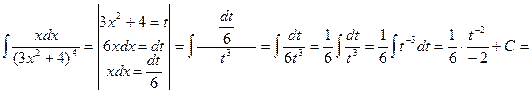
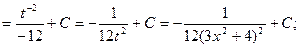
4) 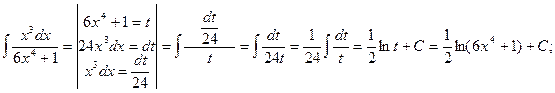
5) 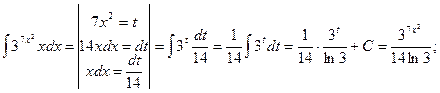
Интегрируя обе части равенства 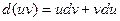 , получим
, получим 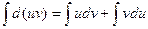
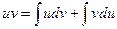 , откуда
, откуда 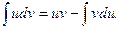
Примеры 16. Найти следующие интегралы:
1) 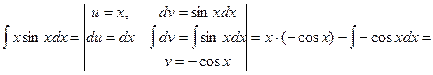
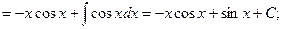
2) 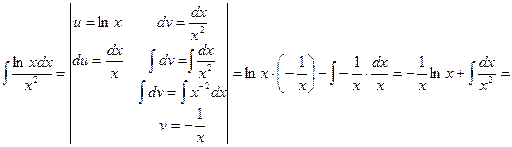
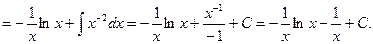
Интегрирование рациональной дроби 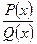 приводится к интегрированию простейших дробей.
приводится к интегрированию простейших дробей.
Пример 17. Найти интегралы:
1) 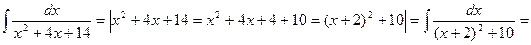
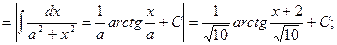
2) 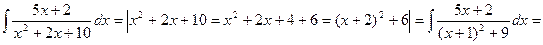
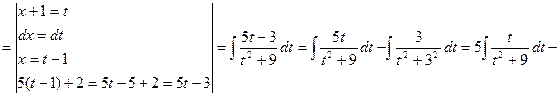

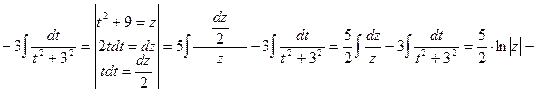
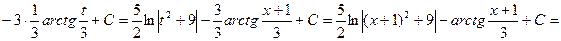
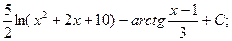
Для вычисления определенного интеграла от функции f(x) в этом случае, когда можно найти соответствующий неопределенный интеграл F(x), служит формула Ньютона-Лейбница:
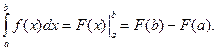
Вычисление определенного интеграла:
Пример 18. Вычислить следующие определенные интегралы
1) 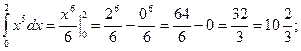
2) 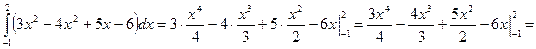
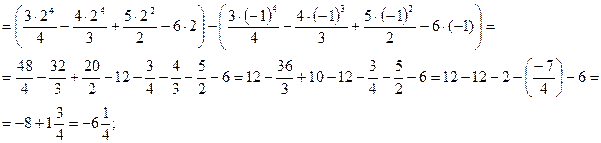
3) 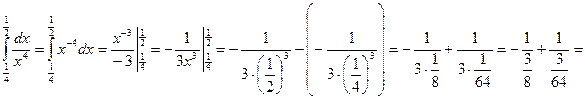
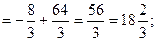
4) 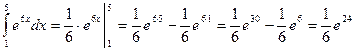
5) 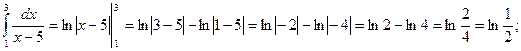
6) 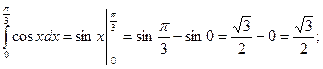
7) 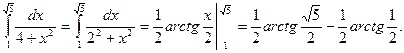
При вычислении определенного интеграла методом замены переменой (способом подстановки) определенный интеграл 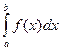 преобразуется с помощью подстановки
преобразуется с помощью подстановки 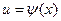 и
и 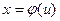 в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной 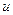 . При этом старые пределы интегрирования
. При этом старые пределы интегрирования 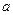 и
и 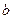 заменяются соответственно новыми пределами интегрирования
заменяются соответственно новыми пределами интегрирования 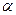 и
и 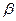 , которые находятся из исходной подстановки.
, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: 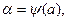
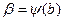 .
.
Из второй подстановки новый пределы интегрирования находятся путем решения уравнений 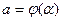 и
и 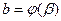 относительно
относительно 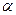 и
и 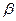 .
.
Таким образом, имеем:
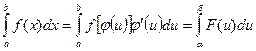
Пример 19. Вычислить определенные интегралы:
1) 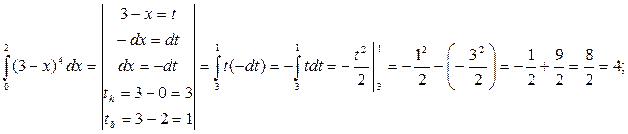
2) 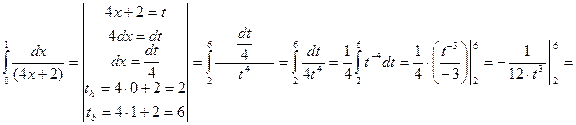
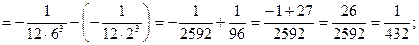
3) 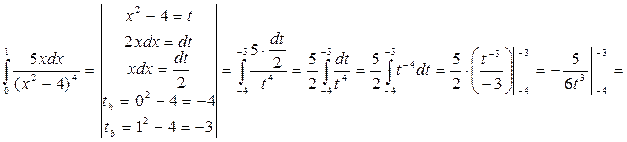
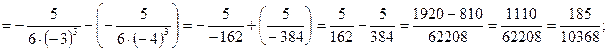
4) 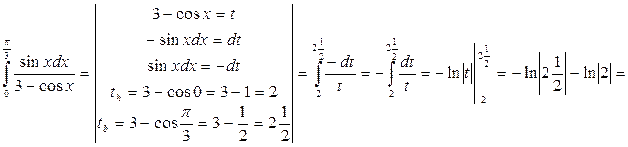
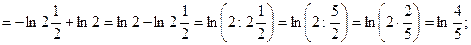
5) 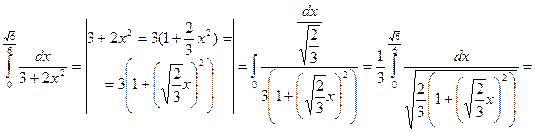
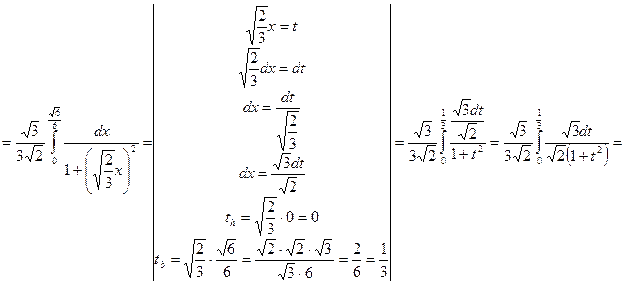
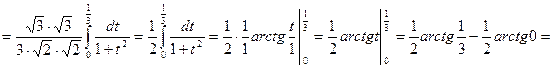
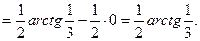
Если функции 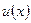 и
и 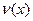 и их производные
и их производные 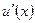 и
и 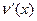 непрерывны в промежутке
непрерывны в промежутке 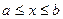 ,то формула интегрирования по частям для определенного интеграла имеет вид
,то формула интегрирования по частям для определенного интеграла имеет вид
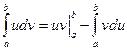
Пример 20. Вычислить интеграл
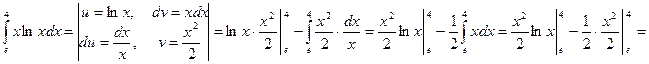
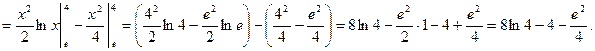
Геометрический смысл определенного интеграла. Приложение интеграла к решению прикладных задач:
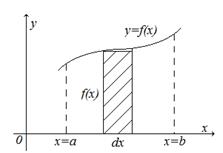 Найдём площадь S криволинейной трапеции, ограниченной кривой
Найдём площадь S криволинейной трапеции, ограниченной кривой 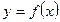 , осью Ox и двумя прямыми x=a и x=b, где
, осью Ox и двумя прямыми x=a и x=b, где 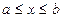 ,
, 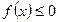 .
.
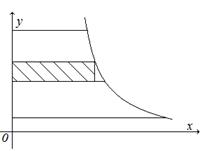 Так как дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой
Так как дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой 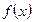 ,т.е.
,т.е. 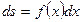 , то интегрируя это равенство в пределах от a до b, получим
, то интегрируя это равенство в пределах от a до b, получим 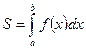 .
.
Если криволинейная трапеция прилегает к оси Oy так, что 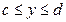 ,
, 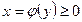 , то дифференциал переменной площади S равен
, то дифференциал переменной площади S равен 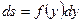 , откуда
, откуда 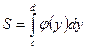 .
.
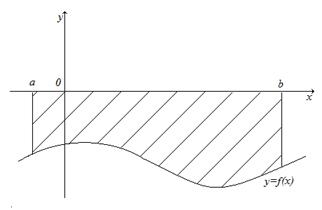 В том случае, когда криволинейная трапеция, ограниченная кривой
В том случае, когда криволинейная трапеция, ограниченная кривой 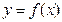 , осью Ox и прямым
, осью Ox и прямым 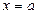 и
и 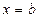 , лежит под осью Ox, площадь находится по формуле
, лежит под осью Ox, площадь находится по формуле 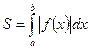 .
.
Если фигура, ограниченная кривой 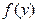 , осью Ox и прямыми
, осью Ox и прямыми 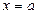 и
и 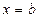 , расположена по обе стороны от оси Ox, то
, расположена по обе стороны от оси Ox, то 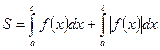 .
.
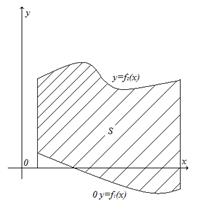
Пусть, наконец, фигура S ограничена двумя пересекающимися кривыми 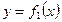 и
и 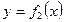 и прямыми
и прямыми 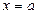 и
и 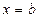 и
и 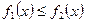 . Тогда её площадь находится по формуле
. Тогда её площадь находится по формуле 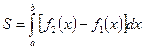 .
.
Пример 21. Вычислите площади фигур, ограниченных указанными линиями:
1) 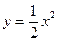 ,
, 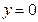 ,
, 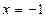 ,
, 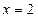
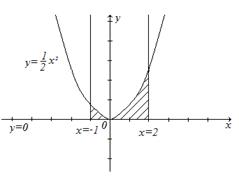 В данном случае требуется вычислить площадь криволинейной трапеции, ограниченной параболой
В данном случае требуется вычислить площадь криволинейной трапеции, ограниченной параболой 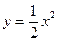 , прямыми
, прямыми 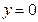 ,
, 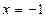 , и
, и 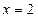 . Посмотрим эти линии.
. Посмотрим эти линии.
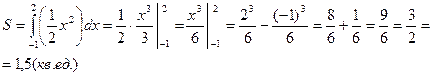
Ответ: 1,5 кв. ед.
2) 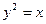 ,
, 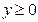 ,
, 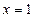 ,
, 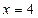
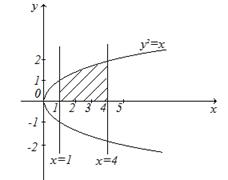
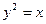
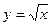
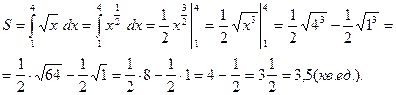
Ответ: 3,5 кв. ед.
3) 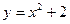 ,
, 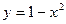 ,
, 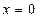 ,
, 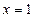 .
.
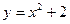 -парабола
-парабола
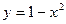 -парабола
-парабола
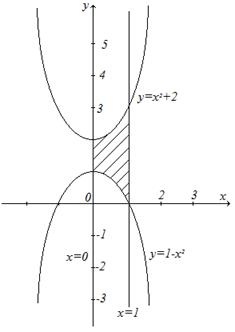
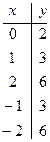
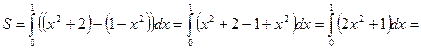
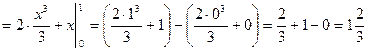 кв. ед.
кв. ед.
Ответ: 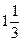 кв. ед.
кв. ед.
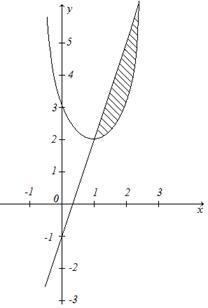 4)
4) 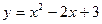 ,
, 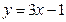 .
.
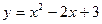 -парабола
-парабола
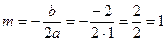 ,
,
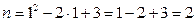 ,
,
(1;2) - вершина параболы
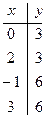
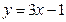 -прямая
-прямая
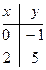
Для нахождения точек пересечения решим систему:
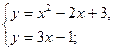
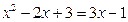 ,
,
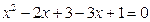 ,
,
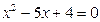 ,
,
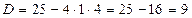 ,
,
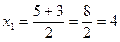 ,
,
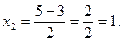
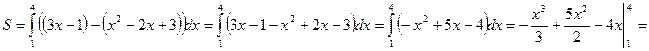
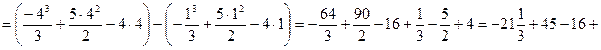
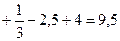 кв. ед.
кв. ед.
Ответ: 9,5 кв. ед.
Вопросы для самопроверки по теме 1.1:
1. Какие неопределённости вы знаете?
2. Назовите 1-й замечательный предел.
3. Назовите второй замечательный предел.
4. Какая точка называется точкой разрыва?
5. Что называется точкой разрыва I рода?
6. Что называется точкой разрыва II рода?
7.Что называется производной функции?
8. Что называется дифференцированием функции?
9. Как найти производную сложной функции?
10. Какая функция называется чётной?
11. Какая функция называется нечётной?
12. Как найти критические точки функции?
13. Общий вид уравнения наклонной асимптоты.
14. В чем заключается сущность метода интегрирования заменой переменной?
15. Назовите формулу интегрирования по частям.
16. Как интегрируются рациональные дроби?
17. В чем суть вычисления определенного интеграла путем замены переменной?
18. Какова формула вычисления определенного интеграла по частям?
19. Какова формула вычисления площади криволинейной трапеции, ограниченой кривой 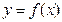 , осью Ox и прямые
, осью Ox и прямые 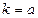 и
и 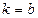 ?
?
20. Какова формула вычисления полощади криволинейной трапеции, ограниченной кривой 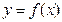 , осью Ox и прямыми
, осью Ox и прямыми 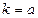 и
и 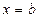 , лежит под осью Ox?
, лежит под осью Ox?
21. Какова площадь фигуры ограниченной двумя пересекающимися кривыми 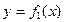 и
и 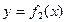 и прямыми
и прямыми 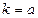 и
и 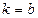 , где
, где 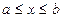 и
и 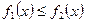 ?
?
Задания для самостоятельного решения по теме 1.1:
1. Вычислить пределы:
1) 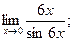
2) 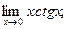
3) 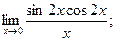
4) 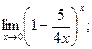
5) 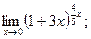
2. Вычислить односторонние пределы:
1) 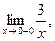
2) 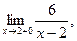
3) 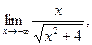
4) 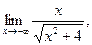
3.Найдите производные функций:
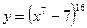
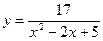
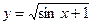
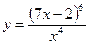
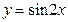
4. Исследовать и построить графики следующих функций:
а) у 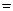 х3+х2-5х+3;
х3+х2-5х+3;
б) у = 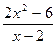 .
.
5. Найдите частные производные следующих функций:
1) 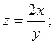
2) 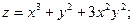
3) 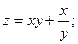
4) 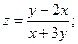
5) 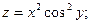
6.Найдите следующие интегралы методом замены переменной:
а) 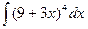
б) 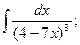
в) 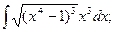
г) 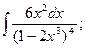
д) 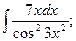
7. Найдите следующие интегралы методом интегрирования на части:
1) 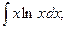
2) 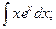
8. Найдите интеграл:
1) 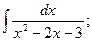
2) 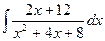
9. Вычислите следующие определенные интегралы:
1) 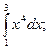
2) 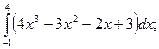
3) 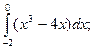
4) 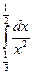 ;
;
5) 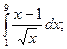
10. Вычислите методом замены переменной следующие определенные интегралы:
1) 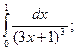
2) 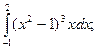
3) 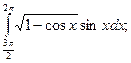
11. Вычислите определенный интеграл, применяя формулу интегрирования по частям.
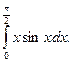
12. Вычислите площади фигур, ограниченных указанными линиями:
1) 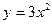 ,
, 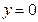 ,
, 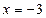 ,
, 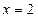 ;
;
2) 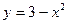 ,
, 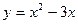 ,
, 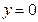 ;
;
 2015-10-16
2015-10-16 880
880








