11.1. Написать уравнение гармонического колебания, если амплитуда его 10 см, максимальная скорость u = 50 см/с, начальная фаза φ = 15˚. Определить период колебания и смещение колеблющейся точки через t = 0,2 с от начала колебаний. Ответ: x(t) = 0,1sin (5t+p /12);
Т = 1,26с;0,095м.
11.2. Гармонические колебания величины s описываются уравнением 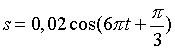 , м. Определить: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний. Ответ: А = 0,02 м; n = 6p с-1; 3 Гц; Т = 0,33 с.
, м. Определить: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний. Ответ: А = 0,02 м; n = 6p с-1; 3 Гц; Т = 0,33 с.
11.3. Уравнение колебаний точки имеет вид 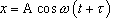 , где
, где 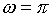 с- 1 ;
с- 1 ; 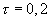 с. Определить период Т и начальную фазу φ колебаний. Ответ: Т = 2 с; φ = 36˚.
с. Определить период Т и начальную фазу φ колебаний. Ответ: Т = 2 с; φ = 36˚.
11.4. Определить период Т, частоту n и начальную фазу φ колебаний, заданных уравнением 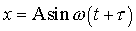 ,
, 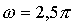 с-1,
с-1, 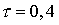 c. Ответ: Т = 0,8 с; n =1,25 Гц; p рад.
c. Ответ: Т = 0,8 с; n =1,25 Гц; p рад.
11.5. Точка совершает колебания по закону 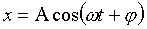 , где А = 4 см. Определить начальную фазу φ, если: 1)
, где А = 4 см. Определить начальную фазу φ, если: 1) 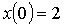 см и
см и 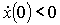 ; 2)
; 2) 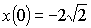 см и
см и 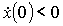 ; 3)
; 3) 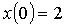 см и
см и 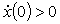 ; 4)
; 4) 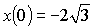 см и
см и 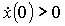 . Ответ: 1) φ1 =
. Ответ: 1) φ1 = 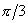 рад; 2) φ2 =
рад; 2) φ2 = 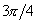 рад; 3) φ3 =
рад; 3) φ3 = 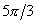 рад; 4) φ4 = =
рад; 4) φ4 = = 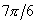 рад.
рад.
11.6. Точка равномерно движется по окружности против часовой стрелки с периодом Т = 6 с. Диаметр d окружности равен 20 см. Написать уравнение движения проекции точки на ось х, проходящую через центр окружности, если в момент времени, принятый за начальный, проекция на ось х равна нулю. Найти смещение х, скорость 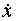 и ускорение
и ускорение 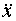 проекции точки в момент
проекции точки в момент 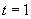 c. Ответ:
c. Ответ: 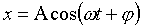 , где А=10 см;
, где А=10 см; 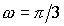 рад/с;
рад/с; 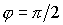 рад;
рад; 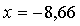 см;
см; 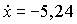 см/с;
см/с; 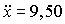 см/с2.
см/с2.
11.7. Определить максимальные значения скорости 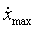 и ускорения
и ускорения 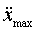 точки, совершающей гармонические колебания с амплитудой
точки, совершающей гармонические колебания с амплитудой 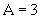 см и угловой частотой
см и угловой частотой 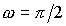 с-1. Ответ: u = 4,71 см/с; а = 7,40 см/с2.
с-1. Ответ: u = 4,71 см/с; а = 7,40 см/с2.
11.8. Точка совершает колебания по закону 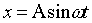 . В некоторый момент времени смещение х 1 точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение х 2 стало равным 8 см. Найти амплитуду А колебаний. Ответ: А = 8,33 см.
. В некоторый момент времени смещение х 1 точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение х 2 стало равным 8 см. Найти амплитуду А колебаний. Ответ: А = 8,33 см.
 2015-10-16
2015-10-16 1385
1385
