· Уравнение гармонических колебаний
X = Acos(ωt+φ), (11.1)
где x – смещение колеблющейся точки от положения равновесия; t – время; A, ω, φ – соответственно амплитуда, угловая частота, начальная фаза колебаний; (ω t+φ) – фаза колебаний в момент t.
· Угловая частота колебаний
ω =2pn, или ω=2p/Τ, (11.2)
где n и Τ – частота и период колебаний.
· Скорость точки, совершающей гармонические колебания
υ = dх / dt = - А ω sin (ωt + φ). (11.3)
· Ускорение при гармонических колебаниях
a = d2x / dt2 = - А ω2 cos (ωt + φ). (11.4)
· Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
A2 = A12 + A22 + 2 A1 A2 cos (φ2 – φ1), (11.5)
где А1 и А2 – амплитуды составляющих колебаний; φ2 и φ1 – их начальные фазы.
· Начальная фаза φ результирующего колебания может быть найдена из формулы
tgφ = (А1sin φ1+A2 sin φ2) / (А1cos φ1+ A2 cos φ2). (11.6)
· Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами n1 и n2,
n = n1 - n2. (11.7)
· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами А1 и А2 и начальными фазами φ1 и φ2:
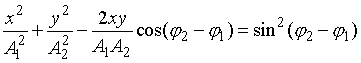 . (11.8)
. (11.8)
Если начальные фазы φ1 и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
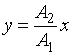 , или
, или 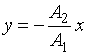 , (11.9)
, (11.9)
то есть точка движется по прямой.
В том случае, если разность фаз Δφ = φ2 – φ1 = p/2, то уравнение принимает вид
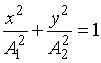 , (11.10)
, (11.10)
то есть точка движется по эллипсу.
· Дифференциальное уравнение гармонических колебаний материальной точки
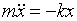 или
или 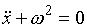 , (11.11)
, (11.11)
где m – масса точки, k – коэффициент квазиупругой силы (k = mω2).
· Полная энергия материальной точки, совершающей гармонические колебания
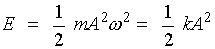 (11.12)
(11.12)
· Период колебаний тела, подвешенного на пружине (пружинный маятник)
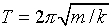 , (11.13)
, (11.13)
где m – масса тела; k – жесткость пружины.
Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
· Период физического маятника
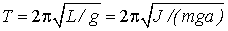 , (11.14)
, (11.14)
где J – момент инерции колеблющегося тела относительно оси колебаний; a – расстояние центра масс маятника от оси колебаний; L = J / (ma) – приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более ≈ 3° ошибка в значении периода не превышает 1 %.
· Период крутильных колебаний тела, подвешенного на упругой нити
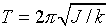 , (11.15)
, (11.15)
где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
· Дифференциальное уравнение затухающих колебаний
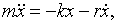 или
или 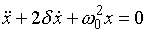 , (11.16)
, (11.16)
где r – коэффициент сопротивления; δ – коэффициент затухания: δ=r/(2m); ω0 – собственная угловая частота колебаний 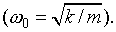
· Уравнение затухающих колебаний
X = А(t)cos(ωt+φ), (11.17)
где А(t) – амплитуда затухающих колебаний в момент t; ω – их угловая частота.
· Угловая частота затухающих колебаний
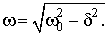 (11.18)
(11.18)
· Зависимость амплитуды затухающих колебаний от времени
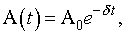 (11.19)
(11.19)
где А0 – амплитуда колебаний в момент 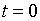 .
.
· Логарифмический декремент колебаний
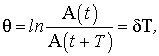 (11.20)
(11.20)
где 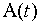 и
и 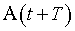 – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
– амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
· Дифференциальное уравнение вынужденных колебаний
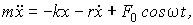 или
или 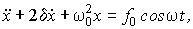 (11.21)
(11.21)
где 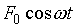 – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 –ее амплитудное значение;
– внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 –ее амплитудное значение; 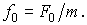
· Амплитуда вынужденных колебаний
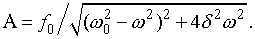 (11.22)
(11.22)
· Резонансная частота и резонансная амплитуда
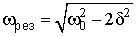 и
и 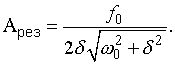 (11.23)
(11.23)
 2015-10-16
2015-10-16 477
477








