Задача 1. Поперечная волна распространяется вдоль упругого шнура со скоростью v = 15 м/с. Период T колебаний точек шнура равен 1,2 с, амплитуда А = 2 см. Определить: 1) длину волны 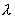 ; 2) фазу jколебаний, смещение
; 2) фазу jколебаний, смещение 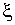 , скорость
, скорость 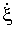 и ускорение
и ускорение 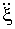 точки, отстоящей на расстоянии х = 45 м от источника волн в момент t = 4 с; 3) разность фаз
точки, отстоящей на расстоянии х = 45 м от источника волн в момент t = 4 с; 3) разность фаз 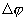 колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях: х 1 = 20 м и х 2 = 30 м.
колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях: х 1 = 20 м и х 2 = 30 м.
Решение
1. Длина волны равна расстоянию, которое волна проходит за один период, и может быть найдена из соотношения (12.2)
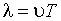
Подставив значения величин 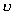 и Т, получим
и Т, получим
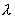 = 18 м.
= 18 м.
2. Запишем уравнение волны (12.1):
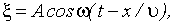
где 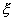 – смещение колеблющейся точки; х – расстояние точки от источника волн;
– смещение колеблющейся точки; х – расстояние точки от источника волн; 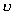 – скорость распространения волн.
– скорость распространения волн.
Фаза колебаний точки с координатой х в момент времени tопределяется выражением, стоящим в уравнении волны под знаком косинуса:
 или
или 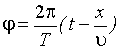 ,
,
где учтено, что 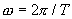 .
.
 2015-10-16
2015-10-16 1363
1363








