При выборе методов обработки существенную роль играют три особенности машинного эксперимента с моделью системы [34,35]:
- возможность получать при моделировании системы на ЭВМ большие выборки позволяет количественно оценить характеристики процесса функционирования системы, но превращает в серьезную проблему хранение промежуточных результатов моделирования;
- сложность исследуемой системы может привести к тому, что априорное суждение о характеристиках процесса функционирования системы, например о типе ожидаемого распределения выходных переменных, является невозможным;
- блочность конструкции машинной модели и раздельное исследование блоков связаны с программной имитацией входных переменных для одной частичной модели по оценкам выходных переменных, полученных на другой частичной модели.
Рассмотрим наиболее удобные для программной реализации методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки (числе реализаций 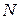 ). Математическое ожидание и дисперсия непрерывной случайной величины
). Математическое ожидание и дисперсия непрерывной случайной величины 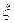 имеют соответственно вид
имеют соответственно вид
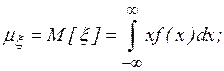
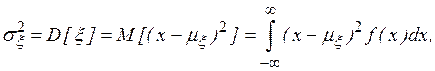
где 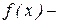 плотность распределения случайной величины
плотность распределения случайной величины 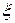 , принимающей значения
, принимающей значения 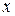 .
.
Для дискретной случайной величины 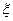 первый начальный и второй центральный моменты будут иметь вид
первый начальный и второй центральный моменты будут иметь вид
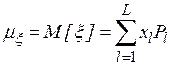
и
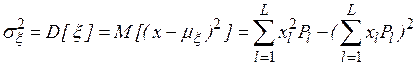 ,
,
где l = 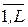 есть количество возможных значений, которые случайная величина может принять.
есть количество возможных значений, которые случайная величина может принять.
При проведении имитационного эксперимента со стохастической моделью системы определить эти моменты нельзя ввиду отсутствия априорной информации о дифференциальном законе распределения. По этой причине вместо моментов при обработке результатов моделирования определяют их оценки, пользуясь предельными теоремами теории вероятностей. Так, в соответствии с теоремой Чебышева, если в 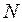 независимых испытаниях наблюдаются значения случайной величины
независимых испытаниях наблюдаются значения случайной величины 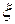 , то при
, то при 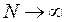 среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию. Таким образом, оценки вероятностных характеристик (1) и (2) будут соответственно иметь вид
среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию. Таким образом, оценки вероятностных характеристик (1) и (2) будут соответственно иметь вид
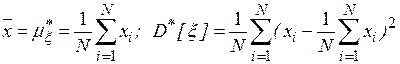 .
.
К качеству оценок, полученных в результате статистической обработки результатов моделирования, предъявляются требования:
- несмещенности, то есть равенства математического ожидания оценке самой вероятностной характеристике:
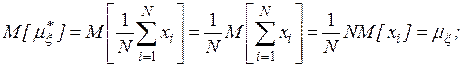
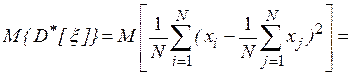
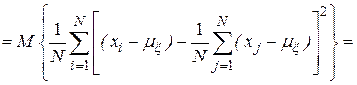
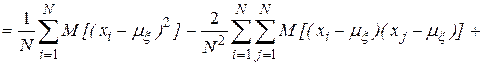
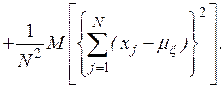
Учитывая, что случайные величины 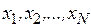 независимы, находим, что
независимы, находим, что
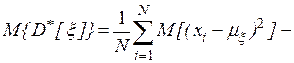
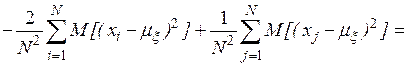
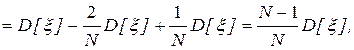
откуда следует, что оценка математического ожидания является несмещенной, а дисперсии – смещенной.
Несмещенную оценку дисперсии можно получить, вычисляя выборочную дисперсию с использованием оценки:

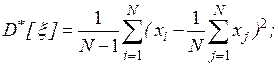
- эффективности оценки, то есть минимальности среднего квадрата ошибки данной оценки 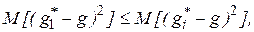 где
где 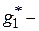 рассматриваемая оценка;
рассматриваемая оценка; 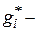 любая другая оценка;
любая другая оценка; 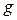 - значение параметра;
- значение параметра;
- состоятельности оценки, то есть ее сходимости по вероятности при 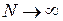 к оцениваемому параметру:
к оцениваемому параметру:
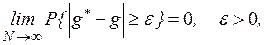
либо, с учетом неравенства Чебышева, достаточное (но не обязательно необходимое) условие выполнения этого неравенства заключается в том, чтобы
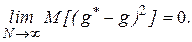
Рассмотрим некоторые особенности статистических методов, используемых для обработки результатов моделирования. При большом числе реализаций 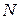 в результате моделирования получается значительный объем информации о состояниях процесса функционирования системы. Поэтому следует так организовать фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались в реальном масштабе времени, то есть без предварительного запоминания всей текущей информации. В качестве таких оценок чаще всего используют частость осуществления некоторого события, среднее значение, выборочные дисперсию, корреляционные моменты и функции, интегральный и дифференциальный законы распределения.
в результате моделирования получается значительный объем информации о состояниях процесса функционирования системы. Поэтому следует так организовать фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались в реальном масштабе времени, то есть без предварительного запоминания всей текущей информации. В качестве таких оценок чаще всего используют частость осуществления некоторого события, среднее значение, выборочные дисперсию, корреляционные моменты и функции, интегральный и дифференциальный законы распределения.
В первом случае в качестве оценки для искомой вероятности 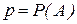 используется частота наступления события
используется частота наступления события 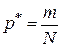 , где
, где 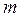 - число случаев наступления события
- число случаев наступления события 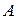 . Данная оценка является состоятельной, несмещенной и эффективной. При ее определении в памяти необходимо накапливать только число
. Данная оценка является состоятельной, несмещенной и эффективной. При ее определении в памяти необходимо накапливать только число 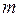 .
.
Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, то есть ее закона распределения. Область возможных значений случайной величины 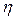 разбивается на
разбивается на 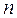 интервалов, после чего определяется количество попаданий
интервалов, после чего определяется количество попаданий 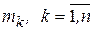 значений случайной величины в каждый интервал. Оценкой для вероятности попадания в каждый интервал с номером
значений случайной величины в каждый интервал. Оценкой для вероятности попадания в каждый интервал с номером 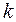 служит величина
служит величина 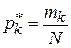 , а в памяти компьютера задействуется всего
, а в памяти компьютера задействуется всего 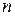 ячеек.
ячеек.
Для оценки математического ожидания случайной величины 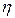 , как уже понятно, накапливается сумма возможных значений случайной величины
, как уже понятно, накапливается сумма возможных значений случайной величины 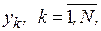 которые она принимает в различных реализациях. Тогда среднее значение будет равно
которые она принимает в различных реализациях. Тогда среднее значение будет равно
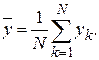
Так как данная оценка является несмещенной и состоятельной,
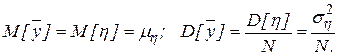 .
.
В качестве оценки дисперсии случайной величины 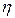 при обработке результатов моделирования целесообразно использовать формулу
при обработке результатов моделирования целесообразно использовать формулу
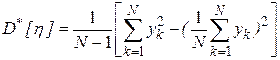 .
.
В этом случае для вычисления дисперсии достаточно накапливать две суммы: значений 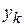 и их квадратов.
и их квадратов.
Для вычисления выборочного корреляционного момента случайных величин 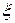 и
и 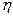 с возможными значениями
с возможными значениями 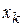 и
и 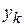 используют выражение
используют выражение
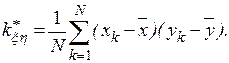
При запоминании в процессе моделирования небольшого числа значений целесообразнее, с точки зрения точности, использовать формулу
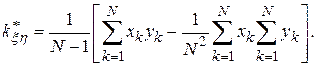
Выборочные авто и взаимокорреляционные функции 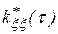 и
и 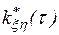 определяются в соответствии с выражениями
определяются в соответствии с выражениями
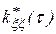
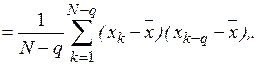
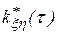
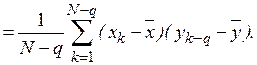
Вычисление производится последовательно – при заданном значении задержки 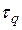 определяется одна точка корреляционной функции. Для получения всей кривой операция повторяется при всех значениях временного сдвига
определяется одна точка корреляционной функции. Для получения всей кривой операция повторяется при всех значениях временного сдвига 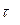 . Общее время прогона модели увеличивается при этом в h раз, где h – количество вычисляемых точек оценки корреляционной функции.
. Общее время прогона модели увеличивается при этом в h раз, где h – количество вычисляемых точек оценки корреляционной функции.
При обработке результатов машинного эксперимента часто возникают задачи определения эмпирического закона распределения случайной величины, проверки однородности распределений, сравнения средних значений и дисперсий переменных, полученных в результате моделирования. Все эти задачи, с точки зрения математической статистики, являются типовыми задачами на проверку статистических гипотез.
Статистическая гипотеза – это утверждение относительно значений одного или более параметров распределения некоторой величины или о самой форме распределения. Принято выбирать две гипотезы: основную или, как ее называют, нулевую 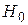 и альтернативную ей
и альтернативную ей 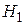 .
.
Статистическая проверка гипотезы – это процедура выяснения справедливости нулевой гипотезы 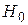 , для чего производится эксперимент (набирается выборка) и далее для принятия или опровержения гипотезы выбирается некоторая контрольная величина
, для чего производится эксперимент (набирается выборка) и далее для принятия или опровержения гипотезы выбирается некоторая контрольная величина 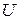 , называемая критерием, характеризующая степень расхождения теоретического и эмпирического распределений. Если в результате проверки гипотеза
, называемая критерием, характеризующая степень расхождения теоретического и эмпирического распределений. Если в результате проверки гипотеза 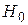 ошибочно отвергается, то с вероятностью
ошибочно отвергается, то с вероятностью 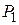 имеет место ошибка первого рода. При проверке обычно задаются величиной
имеет место ошибка первого рода. При проверке обычно задаются величиной 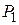 =0,001 – 0,1 и называют это значение уровнем значимости. Величину, обратную уровню значимости
=0,001 – 0,1 и называют это значение уровнем значимости. Величину, обратную уровню значимости 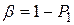 , называют доверительной вероятностью.
, называют доверительной вероятностью.
По результатам выборки вычисляется частное значение критерия 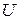 - u. Если u принадлежит критической области, то есть совокупности значений критерия, при которых нулевую гипотезу отвергают, то от гипотезы
- u. Если u принадлежит критической области, то есть совокупности значений критерия, при которых нулевую гипотезу отвергают, то от гипотезы 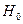 отказываются. В противном случае принято говорить, что полученные наблюдения не противоречат принятой гипотезе.
отказываются. В противном случае принято говорить, что полученные наблюдения не противоречат принятой гипотезе.
Выбор типа теоретического распределения 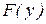 проводится по гистограммам
проводится по гистограммам 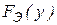 , выведенным на печать или на экран монитора.
, выведенным на печать или на экран монитора.
Рассмотрим особенности использования критериев согласия при обработке результатов моделирования.
Критерий согласия Пирсона (хи-квадрат) предназначен для проверки гипотезы 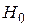 о том, что совокупность эмпирических данных, представляющих собой экспериментально полученный закон распределения некоторой случайной величины, незначительно отличается от той, которую можно ожидать при некотором теоретическом законе распределения. Критерий был предложен Пирсоном в 1903 году и полностью разработан Фишером, который опубликовал в 1924 году таблицы критических величин. Основан на определении в качестве меры расхождения
о том, что совокупность эмпирических данных, представляющих собой экспериментально полученный закон распределения некоторой случайной величины, незначительно отличается от той, которую можно ожидать при некотором теоретическом законе распределения. Критерий был предложен Пирсоном в 1903 году и полностью разработан Фишером, который опубликовал в 1924 году таблицы критических величин. Основан на определении в качестве меры расхождения 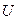 величины
величины
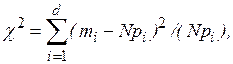
где 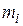 - количество значений случайной величины
- количество значений случайной величины 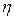 , попавших в
, попавших в 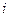 -й подынтервал;
-й подынтервал;
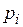 - вероятность попадания случайной величины
- вероятность попадания случайной величины 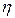 в
в 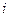 -й подынтервал, вычисленная из теоретического распределения;
-й подынтервал, вычисленная из теоретического распределения;
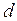 - количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте;
- количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте;
N - объем выборки значений случайной величины 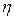 при машинном эксперименте.
при машинном эксперименте.
При 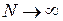 закон распределения величины
закон распределения величины 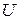 , являющейся мерой расхождения, приближается к закону распределения
, являющейся мерой расхождения, приближается к закону распределения 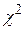 (хи-квадрат) с
(хи-квадрат) с 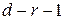 степенями свободы, где
степенями свободы, где 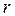 - число параметров теоретического закона распределения.
- число параметров теоретического закона распределения.
Из теоремы Пирсона следует, что какова бы ни была функция распределения 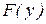 случайной величины
случайной величины 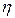 , при
, при 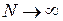 распределение величины
распределение величины 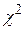 имеет вид
имеет вид
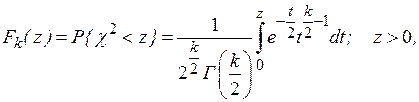
где 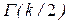 - гамма-функция;
- гамма-функция;
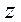 - значение случайной величины
- значение случайной величины 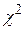 ;
;
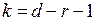 - число степеней свободы. Функции распределения
- число степеней свободы. Функции распределения 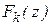 табулированы.
табулированы.
По таблице 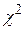 -распределений, приведенной в большинстве математических справочников, находят критическое значение
-распределений, приведенной в большинстве математических справочников, находят критическое значение 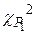 для уровня значимости
для уровня значимости 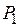 и числа степеней свободы
и числа степеней свободы 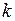 . Если
. Если 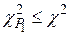 , то гипотеза отвергается.
, то гипотеза отвергается.
Применяя метод проверки гипотез по критерию согласия 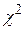 , следует помнить, что значения наблюдаемых частот для каждой группы или интервала должны быть от пяти и более, в противном случае смежные группы или интервалы должны объединяться.
, следует помнить, что значения наблюдаемых частот для каждой группы или интервала должны быть от пяти и более, в противном случае смежные группы или интервалы должны объединяться.
Рассмотрим в качестве примера применения критерия проверку распределения относительных частот запросов сайта за одночасовой интервал, приведенное в таблице 17.1.
Если построить гистограмму в соответствии с данными, приведенными в таблице, то видно, что экспериментальное распределение близко к распределению Пуассона. И действительно, когда вероятность некоторого события для одного временного интервала такая же, как и для любого другого, а осуществление какого-либо события не оказывает влияния на вероятность его повторного повторения, имеется веское основание ожидать распределение Пуассона. Дополнительные основания для этого мы получаем, если в любом интервале времени имеет место высокая вероятность появления нулевого числа событий и если среднее число событий в каждом временном интервале мало.
Т а б л и ц а 17.1
| Число запросов | Число одночасовых интервалов с соответствующим числом запросов | Относительная частота |
| 0,619 | ||
| 0,279 | ||
| 0,078 | ||
| 0,018 | ||
| 0,004 | ||
| 0,002 | ||
| Объем выборки 509 | 1,000 |
Известно, что распределение Пуассона выражается формулой
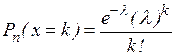
 ,
,
где 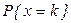 =
= 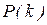 - вероятность наступления k событий;
- вероятность наступления k событий;
e = 2,71828;
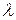 - положительная константа, являющаяся для закона Пуассона одновременно и математическим ожиданием, и дисперсией.
- положительная константа, являющаяся для закона Пуассона одновременно и математическим ожиданием, и дисперсией.
На основании данных табл. 17.1 определим оценки математического ожидания и дисперсии:
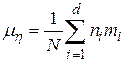 ;
;
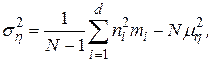
где 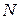 - как и ранее, полный объем выборки,
- как и ранее, полный объем выборки, 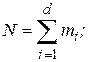
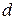 - число групп (интервалов) выборки;
- число групп (интервалов) выборки;
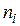 - значение
- значение 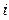 -й группы.
-й группы.
Вычисления сведем в таблицу 17.2
Т а б л и ц а 17.2
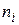 | 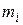 | 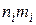 | 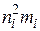 |
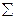 |
и окончательно получим
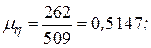
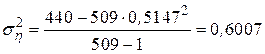 .
.
Полученные результаты, действительно, оказались близки друг другу. Примем, что 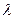 равна средней величине между оценками математического ожидания и дисперсии, то есть
равна средней величине между оценками математического ожидания и дисперсии, то есть
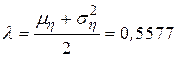
и гипотезу 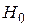 сформулируем следующим образом: не имеется существенных различий между наблюдаемыми данными и данными, которые получаются из распределения Пуассона с математическим ожиданием и дисперсией
сформулируем следующим образом: не имеется существенных различий между наблюдаемыми данными и данными, которые получаются из распределения Пуассона с математическим ожиданием и дисперсией 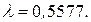 Подставив в формулу для распределения Пуассона полученное значение
Подставив в формулу для распределения Пуассона полученное значение 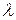 и последовательно
и последовательно 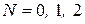 и т.д., получим данные, представленные в таблице 17.3.
и т.д., получим данные, представленные в таблице 17.3.
Для получения значения ожидаемой частоты для каждого подынтервала умножаем соответствующую величину 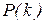 на 509. Следующий шаг – определение критического значения величины
на 509. Следующий шаг – определение критического значения величины 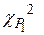 для выбранного доверительного уровня 0,95 и числа степеней свободы 4 – 1 – 1 = 2 из таблицы критических величин, приведенных в справочнике. Находим, что табличное значение
для выбранного доверительного уровня 0,95 и числа степеней свободы 4 – 1 – 1 = 2 из таблицы критических величин, приведенных в справочнике. Находим, что табличное значение 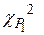 = 5,99, что больше расчетной величины
= 5,99, что больше расчетной величины 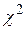 =5,10. Таким образом, гипотеза
=5,10. Таким образом, гипотеза 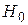 принимается.
принимается.
Т а б л и ц а 17.3
| k | P(k) | 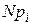 | 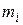 | 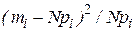 |
| 0,571 | 1,98 | |||
| 0,319 | 2,47 | |||
| 0,089 | 0,56 | |||
| 0,017 | ||||
| 0,003 | 0,09 | |||
| 0,001 | ||||
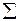 | 1,000 | 5,10 |
Последние три группы значений в нашем расчете были объединены с тем, чтобы получить значение частоты не менее 5 в каждой группе; вместо исходных 6 групп мы получили 4.
Критерий согласия Колмогорова - Смирнова. Основан на выборе в качестве меры расхождения 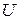 величины
величины 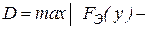
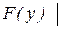 .
.
Из теоремы Колмогорова следует, что 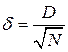 при
при 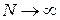 имеет функцию распределения
имеет функцию распределения 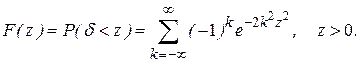
Если вычисленное на основе экспериментальных данных значение 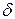 меньше, чем табличное значение при выбранном уровне значимости, то гипотезу
меньше, чем табличное значение при выбранном уровне значимости, то гипотезу 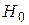 принимают, в противном случае расхождение между
принимают, в противном случае расхождение между 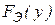 и
и 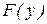 считается неслучайным и гипотеза
считается неслучайным и гипотеза 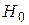 отвергается.
отвергается.
Критерий целесообразно применять в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования критерия – необходимость фиксации в памяти ПК для определения D всех статистических частот в целях их упорядочения в порядке возрастания.
При оценке адекватности машинной модели возникает необходимость проверки гипотезы 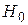 , заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей
, заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей 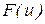 и
и 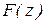 , из которых извлечены выборки, являются непрерывными функциями своих аргументов
, из которых извлечены выборки, являются непрерывными функциями своих аргументов 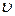 и
и 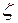 , то для проверки гипотезы
, то для проверки гипотезы 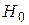 можно использовать критерий согласия Смирнова, применение которого сводится к следующему.
можно использовать критерий согласия Смирнова, применение которого сводится к следующему.
По имеющимся результатам вычисляют эмпирические функции распределения 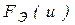 и
и 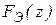 и определяют
и определяют
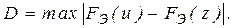
Затем при заданном уровне значимости 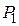 находят допустимое отклонение
находят допустимое отклонение
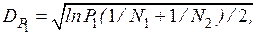
где 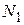 и
и 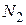 - объемы сравниваемых выборок.
- объемы сравниваемых выборок.
Теперь проводится сравнение значений 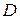 и
и 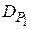 ; если
; если 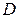 >
> 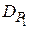 , то нулевая гипотеза
, то нулевая гипотеза 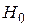 о тождественности законов распределения
о тождественности законов распределения 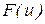 и
и 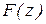 с доверительной вероятностью
с доверительной вероятностью 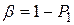 отвергается.
отвергается.
Для иллюстрации вновь рассмотрим данные, приведенные в таблице 17.1. В данном случае гипотеза 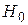 , как и ранее, состоит в том, что не имеется существенных различий между наблюдаемыми данными и теми, которые должны получаться в случае распределения Пуассона. Получим два интегральных распределения – из наблюдаемых данных и из теоретического распределения – и найдем абсолютные разности для всех групп значения случайной величины, как показано в таблице 17.4.
, как и ранее, состоит в том, что не имеется существенных различий между наблюдаемыми данными и теми, которые должны получаться в случае распределения Пуассона. Получим два интегральных распределения – из наблюдаемых данных и из теоретического распределения – и найдем абсолютные разности для всех групп значения случайной величины, как показано в таблице 17.4.
Т а б л и ц а 17.4
| Число запросов | Наблюдаемая частота | Наблюдаемая вероятность | Теоретическая вероятность | Интегральная вероятность II | Интегральная вероятность III | Абсолютная разность | |
| 0,619 | 0,571 | 0,619 | 0,571 | 0,048 | |||
| 0,279 | 0,319 | 0,898 | 0,890 | 0,008 | |||
| 0,078 | 0,089 | 0,976 | 0,979 | 0,003 | |||
| 0,018 | 0,017 | 0,994 | 0,996 | 0,002 | |||
| 0,004 | 0,003 | 0,998 | 0,999 | 0,001 | |||
| 0,002 | 0,001 | 1,000 | 1,000 | 0,000 |
Наибольшая абсолютная разность 0,048 получается в группе, соответствующей нулевому числу запросов. Именно эту разность надо сравнить с критическим значением, найденным из таблиц и равным при N 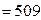 и
и 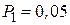
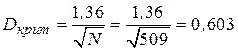 .
.
Так как полученная нами наибольшая разность 0,048 не превышает критического значения, то и в этом случае принимается решение о том, что экспериментальное распределение подчиняется закону Пуассона.
Сравнение рассмотренных критериев, направленных на решение однородных задач, приводит к заключению о том, что критерий 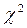 предпочтителен для больших выборок (более 100), в то время как критерий Колмогорова – Смирнова предпочтителен при
предпочтителен для больших выборок (более 100), в то время как критерий Колмогорова – Смирнова предпочтителен при 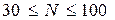 .
.
Критерий согласия Стьюдента. Сравнение средних значений для двух независимых выборок, взятых из нормальных совокупностей с неизвестными, но равными дисперсиями 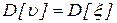 , сводится к проверке нулевой гипотезы
, сводится к проверке нулевой гипотезы 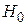 :
: 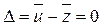 на основании критерия согласия Стьюдента (t- критерия). Проверка по этому критерию сводится к выполнению следующих действий. Вычисляют оценку
на основании критерия согласия Стьюдента (t- критерия). Проверка по этому критерию сводится к выполнению следующих действий. Вычисляют оценку
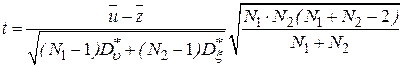 ,
,
где 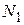 и
и 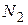 – объемы выборок для оценки
– объемы выборок для оценки 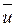 и
и 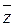 соответственно;
соответственно;
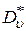 и
и 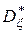 – оценки дисперсий соответствующих выборок.
– оценки дисперсий соответствующих выборок.
Затем определяют число степеней свободы 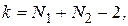 выбирают уровень значимости
выбирают уровень значимости 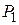 и по таблицам находят значение
и по таблицам находят значение 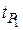 . Расчетное значение сравнивается с табличным и если
. Расчетное значение сравнивается с табличным и если 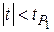 , то гипотеза
, то гипотеза 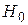 не опровергается результатами машинного эксперимента.
не опровергается результатами машинного эксперимента.
Чувствительность критерия к «нормальной распределенности» величин 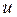 и
и 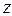 невелика. Он применим, если их распределения не имеют несколько вершин и не слишком ассиметричны.
невелика. Он применим, если их распределения не имеют несколько вершин и не слишком ассиметричны.
Критерий согласия Фишера предназначен для проверки нулевой гипотезы о равенстве дисперсий двух случайных величин при условии, что последние распределены нормально.
Гипотеза такого рода имеет большое значение в технических приложениях, так как дисперсия есть мера таких характеристик, как погрешности измерительных приборов, точность технологических процессов, точность попадания при стрельбе и пр. Пусть необходимо сравнить две дисперсии 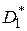 и
и 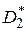 , полученные при обработке результатов моделирования и имеющие
, полученные при обработке результатов моделирования и имеющие 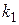 и
и 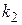 степеней свободы соответственно. Для того чтобы опровергнуть нулевую гипотезу
степеней свободы соответственно. Для того чтобы опровергнуть нулевую гипотезу 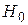 :
: 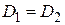 , необходимо при уровне значимости
, необходимо при уровне значимости 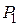 показать расхождение между
показать расхождение между 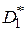 и
и 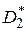 . При условии независимости выборок, взятых из нормальных совокупностей, в качестве критерия используется распределение Фишера (F -критерий), равное отношению дисперсий
. При условии независимости выборок, взятых из нормальных совокупностей, в качестве критерия используется распределение Фишера (F -критерий), равное отношению дисперсий 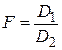 или
или 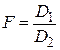 (большая дисперсия должна быть в числителе).
(большая дисперсия должна быть в числителе).
Алгоритм применения критерия Фишера следующий:
- вычисляется выборочное отношение 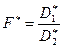 ;
;
- определяется число степеней свободы 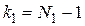 и
и 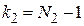 , где
, где 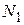 и
и 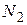 - объемы выборок для оценок
- объемы выборок для оценок 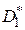 и
и 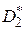 соответственно;
соответственно;
- при выбранном уровне значимости 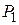 для величины
для величины 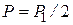 и величин
и величин 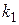 и
и 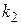 по таблице F -распределения находятся значения
по таблице F -распределения находятся значения 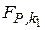 и
и 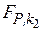 ;
;
- если вычисленное по выборке значение 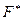 , больше этих критических значений, то нулевая гипотеза
, больше этих критических значений, то нулевая гипотеза 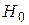 :
: 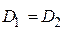 должна быть отклонена с вероятностью ошибки первого рода
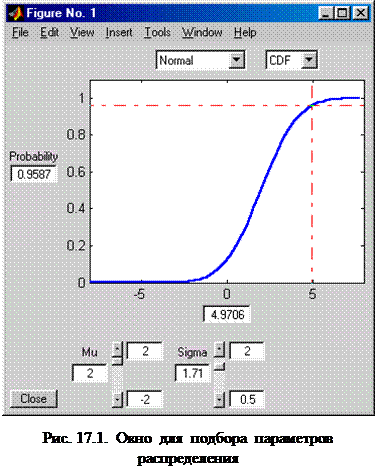
должна быть отклонена с вероятностью ошибки первого рода 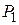 .
.
В MATLABе для подбора вида закона распределения в максимальной степени соответствующего полученной гистограмме следует последовательно ввести три команды: n=hist(y,m), bar(n./length(y)) и disttool. Первая делит диапазон значений наблюдаемой переменной y на m равных интервалов и записывает в матрицу n число элементов, попавших в каждый из них. Вторая – вычисляет относительную частоту попадания в каждый интервал и выводит графическое представление полученной гистограммы. Третья – открывает диалоговое окно, обеспечивающее выбор и настройку параметров стандартных распределений (рис. 17.1), содержащее следующие элементы:
- поле вывода графика закона распределения (cdf -интегрального, pdf- дифференциального), в котором отображается визир предназначенный для точного определения координат;
- раскрывающийся список для выбора вида закона распределения (19 вариантов);
- раскрывающийся список для выбора плотности вероятностей или функции распределения;
- ползунки для изменения значений параметров распределения;
- поля ввода/отображения координат точек графика и параметров распределения.
Для отыскания распределения вероятностей, соответствующего экспериментально полученному, следует выбрать в раскрывающимся списке похожее распределение, учитывая, что его вид в значительной степени зависит от численных значений параметров распределения. Если распределение, полученное в результате проведения модельного эксперимента, близко к нормальному, существует возможность проверки близости его к аппроксимирующему закону распределения. Функция normlot(y) выводит график соответствия, который тем лучше аппроксимируется прямой линией, чем ближе экспериментальные данные согласуются с подобранным нормальным распределением.
Следующий этап обработки экспериментально полученной информации – проверка статистических гипотез. Проверка гипотезы о том, что наблюдаемая величина распределена по нормальному закону с известным СКО и математическим ожиданием равным M, осуществляется с помощью функции ztest, которая может принять одно из двух возможных значений: 0 – если гипотезу следует принять и 1 – гипотезу следует отвергнуть. В качестве дополнительной информации функция ztest формирует величину SIG, которая отражает степень достоверности нулевой гипотезы 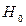 - чем меньше SIG, тем больше доверия
- чем меньше SIG, тем больше доверия 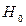 . Аналогичную задачу позволяет решить и функция ttest, которая в качестве дополнительной информации выдает значение условной вероятности того, что используемый статистический критерий примет некоторое значение в предположении, что нулевая гипотеза верна. Величина этой условной вероятности в зарубежной литературе по статистике называется p-value (р-значение). Если p-value оказывается меньше уровня значимости, то нулевая гипотеза отвергается. В качестве примера рассмотрим задачу об определении среднего числа покупателей некоей торговой точки в час пик в четную и нечетную недели. В результате натурного эксперимента были получены следующие результаты по подсчету количества покупателей, посетивших магазин в рабочие дни недели (включая субботу) с 17 до 18 часов соответственно, на четной и нечетной неделях: chet = [26,30,25,29,20,28]; nechet = [24,28,30,25,32,26]. Необходимо проверить гипотезу о том, что среднее количество покупателей остается неизменным независимо от номера недели. Вычислим среднее число покупателей на четной неделе: chislo = mean (chet). Величину chislo используем при обращении к функции ttest, при этом уровень значимости по умолчанию равен 0,05: [H, SIG] = ttest(nechet, chislo). В результате работы функции получим: H = 0, SIG = 0.3964. Это означает, что принятую гипотезу следует принять, однако степень ее достоверности средняя.
. Аналогичную задачу позволяет решить и функция ttest, которая в качестве дополнительной информации выдает значение условной вероятности того, что используемый статистический критерий примет некоторое значение в предположении, что нулевая гипотеза верна. Величина этой условной вероятности в зарубежной литературе по статистике называется p-value (р-значение). Если p-value оказывается меньше уровня значимости, то нулевая гипотеза отвергается. В качестве примера рассмотрим задачу об определении среднего числа покупателей некоей торговой точки в час пик в четную и нечетную недели. В результате натурного эксперимента были получены следующие результаты по подсчету количества покупателей, посетивших магазин в рабочие дни недели (включая субботу) с 17 до 18 часов соответственно, на четной и нечетной неделях: chet = [26,30,25,29,20,28]; nechet = [24,28,30,25,32,26]. Необходимо проверить гипотезу о том, что среднее количество покупателей остается неизменным независимо от номера недели. Вычислим среднее число покупателей на четной неделе: chislo = mean (chet). Величину chislo используем при обращении к функции ttest, при этом уровень значимости по умолчанию равен 0,05: [H, SIG] = ttest(nechet, chislo). В результате работы функции получим: H = 0, SIG = 0.3964. Это означает, что принятую гипотезу следует принять, однако степень ее достоверности средняя.
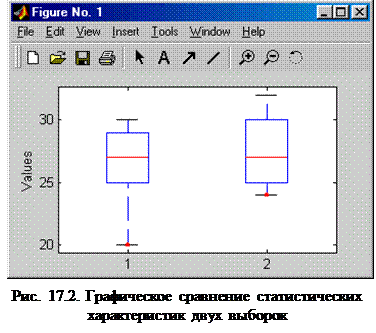
Выборки chet и nechet можно представить графически с помощью функции boxplot(y), параметр у в которой представляет собой матрицу со столбцами, содержащими значения исследуемых выборок. Для получения такой графической интерпретации в командном окне MATLAB следует ввести следующую последовательность команд.
- chet = chet’ – транспонирование вектора chet;
- nechet = nechet’ – транспонирование вектора nechet;
 - y = [chet, nechet] – объединение вектор-столбцов в матрицу;
- y = [chet, nechet] – объединение вектор-столбцов в матрицу;
- boxplot(y) – получение графической интерпретации и вывод картинки на экран. Для рассматриваемого примера получим график, приведенный на рис. 17.2.
Возможность фиксации при моделировании системы на ПК значений параметров и их статистическая обработка для получения интересующих экспериментатора характеристик позволяют провести объективный анализ связей между этими параметрами. Для решения этой задачи существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик. В случаях, когда связь легко обнаруживается или заранее известна, эти методы очевидны. В противоположном случае мы можем столкнуться с необходимостью ввести некоторую гипотезу о характере функциональной зависимости, то есть аппроксимировать ее некоторым относительно простым математическим выражением.
Для поиска математических функциональных зависимостей между двумя или более переменными по накопленным экспериментальным данным весьма полезны методы регрессионного, корреляционного и дисперсионного анализа.
Регрессионный анализ дает возможность построить, исходя из имеющейся совокупности экспериментальных данных, уравнение их связывающее. Иными словами, регрессионный анализ позволяет установить наличие возможной причинной связи между переменными либо предсказать значение эндогенной переменной по значениям независимых переменных.
Корреляционный анализ позволяет судить о том, насколько хорошо экспериментальные точки согласуются с выбранным уравнением («ложатся» на соответствующую кривую). Его результаты позволяют делать статистические выводы о степени зависимости между переменными.
Дисперсионный анализ позволяет оценивать влияние на наблюдаемую переменную произвольного числа факторов. Если фактор один, то анализ однофакторный, в противном случае – многофакторный.
Рассмотрим их последовательно.
Первым шагом при выводе уравнения, аппроксимирующего требуемую зависимость, является сбор данных, отражающих соответствующие значения рассматриваемых переменных. Пусть, например, мы предполагаем, что выход некоторого химического процесса является функцией количества катализатора, вводимого в реактор. Обозначим через 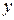 величину выхода и через
величину выхода и через 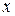 количество вводимого катализатора. Тогда из данных, регистрировавшихся прежде или полученных в результате эксперимента, можно взять выборку объемом
количество вводимого катализатора. Тогда из данных, регистрировавшихся прежде или полученных в результате эксперимента, можно взять выборку объемом 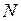 значений
значений 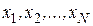 и
и 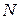 соответствующих значений
соответствующих значений 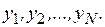
Следующий шаг – это нанесение точек с координатами 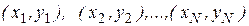 на график в прямоугольной системе координат. В результате мы получим так называемую диаграмму разброса, из которой часто удается чисто визуально найти плавную кривую, аппроксимирующую функциональную зависимость.
на график в прямоугольной системе координат. В результате мы получим так называемую диаграмму разброса, из которой часто удается чисто визуально найти плавную кривую, аппроксимирующую функциональную зависимость.
Если это сделать невозможно, то определим, что следует понимать под «наилучшей» подгонкой кривой. Наложим на диаграмму разброса лекало или гибкую линейку и попытаемся провести кривую так, чтобы она проходила «посередине», то есть все точки, не попавшие на кривую, были бы от нее на одинаковом минимальном расстоянии. Недостаток этого способа заключается в том, что каждый экспериментатор будет получать свои собственные кривые и аппроксимирующие их уравнения. Поэтому хотелось бы выработать такой критерий, который был бы объективно наилучше приближен и имел сравнительно простое математическое представление. Наиболее часто здесь используется метод наименьших квадратов, который формализует процедуру подбора аппроксимирующей кривой на глаз. Суть метода заключается в том, что определяется разница между экспериментально определенными значениями 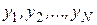 и соответствующими значениями, лежащими на теоретической кривой. Обозначим эту разницу символом
и соответствующими значениями, лежащими на теоретической кривой. Обозначим эту разницу символом 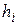 и будем называть ее отклонением. Это отклонение может быть положительным, отрицательным и нулевым. Тогда мерой качества приближения теоретической кривой к экспериментальным данным можно считать сумму абсолютных отклонений
и будем называть ее отклонением. Это отклонение может быть положительным, отрицательным и нулевым. Тогда мерой качества приближения теоретической кривой к экспериментальным данным можно считать сумму абсолютных отклонений 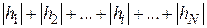 . Поскольку отклонения могут быть положительными или отрицательными, с математической точки зрения проще возвести их значения в квадрат и в дальнейшем иметь дело с квадратичными отклонениями. Сумма последних, очевидно, даст такую же хорошую меру качества приближения.
. Поскольку отклонения могут быть положительными или отрицательными, с математической точки зрения проще возвести их значения в квадрат и в дальнейшем иметь дело с квадратичными отклонениями. Сумма последних, очевидно, даст такую же хорошую меру качества приближения.
Будем поэтому считать, что из всех возможных аппроксимирующих кривых кривой наилучшего приближения для данной совокупности экспериментальных точек будет та, для которой сумма 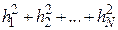 минимальна.
минимальна.
Математический метод, обеспечивающий такую подгонку выбранной кривой, при которой экспериментальные точки ложатся на нее лучшим образом в смысле критерия наименьших квадратов, называется регрессионным анализом. Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок.
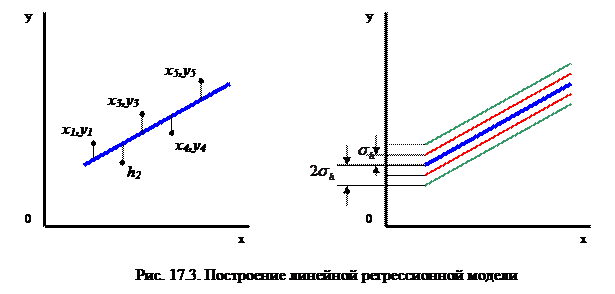
Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На левом рис. 1 показаны точки 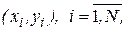 полученные в машинном эксперименте с моделью. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии
полученные в машинном эксперименте с моделью. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии
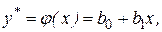
где 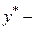 величина, предсказываемая регрессионной моделью.
величина, предсказываемая регрессионной моделью.
Требуется получить такие значения коэффициентов  и
и 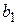 , при которых сумма квадратов ошибок является минимальной. Ошибка в соответствии с рисунком определяется как расстояние по вертикали от этой точки до линии регрессии
, при которых сумма квадратов ошибок является минимальной. Ошибка в соответствии с рисунком определяется как расстояние по вертикали от этой точки до линии регрессии 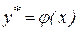 . Обозначим
. Обозначим 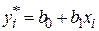 . Тогда выражение для ошибок будет иметь вид
. Тогда выражение для ошибок будет иметь вид 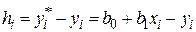 , а функция ошибки
, а функция ошибки
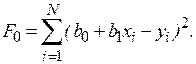
Для получения  и
и 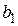 , при которых указанная функция является минимальной, применяются обычные методы математического анализа. Условием минимума являются
, при которых указанная функция является минимальной, применяются обычные методы математического анализа. Условием минимума являются 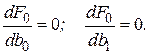
Дифференцируя 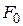 , получаем
, получаем
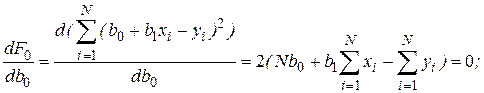
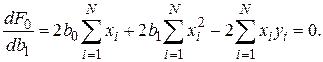
Решая систему этих двух линейных алгебраических уравнений, можно получить значения 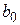 и
и 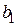 . В матричном представлении эти уравнения имеют вид
. В матричном представлении эти уравнения имеют вид
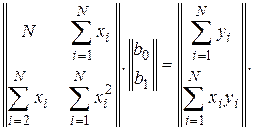
Окончательно получаем
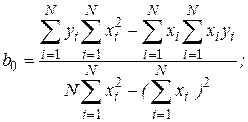
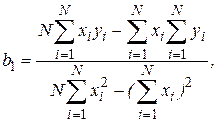
где 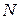 - число реализаций при моделировании системы.
- число реализаций при моделировании системы.
Таким образом, при наличии совокупности данных, состоящей из соответствующих значений 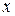 и
и 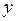 , можно легко вычислить значения
, можно легко вычислить значения 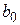 и
и 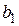 . Так, для случая, показанного на левом графике,
. Так, для случая, показанного на левом графике,
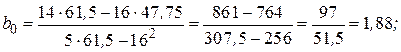
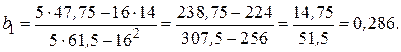
Следовательно, 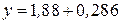
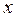 .
.
Полученные соотношения для коэффициентов требуют минимального объема памяти ПК для обработки результатов моделирования.
Мерой ошибки регрессионной модели служит среднеквадратическое отклонение
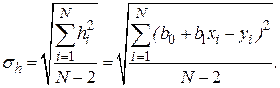
Для нормально распределенных процессов приблизительно 67 % точек находится в пределах одного отклонения 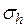 от линии регрессии и 95 % точек – в пределах
от линии регрессии и 95 % точек – в пределах 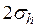 , как показано на правой части рисунка. Для проверки точности оценок
, как показано на правой части рисунка. Для проверки точности оценок 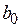 и
и 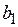 регрессионной модели могут быть использованы критерии Фишера (F -распределение) и Стьюдента (t -распределение). Аналогично могут быть определены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.
регрессионной модели могут быть использованы критерии Фишера (F -распределение) и Стьюдента (t -распределение). Аналогично могут быть определены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.
Наилучшее приближение кривой (или прямой) к экспериментальным данным вовсе не означает, что реально существующая физическая зависимость наилучшим образом описывается аппроксимирующим уравнением, соответствующим именно этой прямой (кривой).
Таблица 17.5
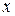 | 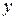 | 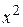 | 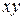 |
| 1,0 | 2,5 | 1,0 | 2,5 |
| 2,5 | 2,0 | 6,25 | 5,0 |
| 3,0 | 3,0 | 9,0 | 9,0 |
| 4,5 | 2,5 | 20,25 | 11,25 |
| 5,0 | 4,0 | 20,0 | |
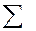 16 16 | 61,5 | 47,75 |
Для оценки того, насколько хорошо теоретическая прямая (кривая) в действительности согласуется с экспериментальными данными, необходимо ввести понятие корреляции, что дает возможность судить о том, насколько тесно ложатся экспериментальные точки на аппроксимирующую кривую. Если регрессия определяет предполагаемое соотношение между переменными, то корреляция показывает, насколько хорошо это соотношение отражает действительность.
С помощью корреляционного анализа исследователь может установить, насколько тесна связь между двумя и более случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы. Корреляционный анализ результатов моделирования сводится к оценке разброса значений 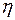 относительно среднего значения
относительно среднего значения 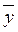 , то есть к оценке силы корреляционной связи. Существование этих связей и их тесноту для схемы корреляционного анализа
, то есть к оценке силы корреляционной связи. Существование этих связей и их тесноту для схемы корреляционного анализа 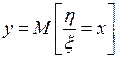 можно выразить при наличии линейной связи между исследуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции
можно выразить при наличии линейной связи между исследуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции
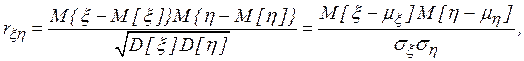
то есть второй смешанный центральный момент делится на произведение средних квадратичных отклонений, чтобы иметь безразмерную величину, инвариантную относительно единиц измерения рассматриваемых случайных величин.
Оценка коэффициента корреляции, очевидно, будет иметь вид
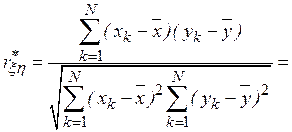
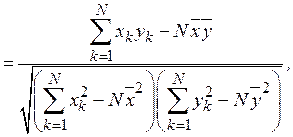
при котором требуются минимальные затраты машинной памяти на обработку результатов моделирования. Получаемый при этом выборочный коэффициент корреляции 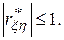 При сделанных предположениях
При сделанных предположениях 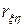 = 0 свидетельствует о взаимной независимости случайных переменных
= 0 свидетельствует о взаимной независимости случайных переменных 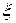 и
и 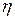 . При
. При 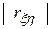 = 1 случайные переменные
= 1 случайные переменные 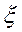 и
и 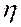 линейно зависят друг от друга, причем если
линейно зависят друг от друга, причем если 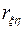
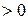 , то говорят о положительной корреляции, то есть большие значения одной случайной величины соответствуют большим значениям другой. Случай
, то говорят о положительной корреляции, то есть большие значения одной случайной величины соответствуют большим значениям другой. Случай 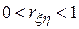 соответствует либо наличию линейной корреляции с рассеянием, либо наличию нелинейной корреляции результатов моделирования.
соответствует либо наличию линейной корреляции с рассеянием, либо наличию нелинейной корреляции результатов моделирования.
Для случая простой линейной регрессионной задачи (т.е. для случая, когда имеются одна зависимая и одна независимая переменные, связанные между собой линейно, коэффициент корреляции вычисляется по формуле
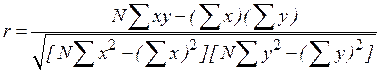 .
.
Используя данные из вышеприведенной таблицы и добавляя столбец для 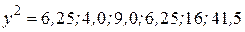 , вычислим по последней формуле значение коэффициента корреляции
, вычислим по последней формуле значение коэффициента корреляции
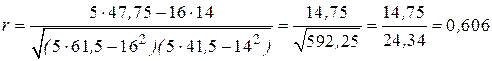 .
.
Для того чтобы оценить точность полученной при обработке результатов моделирования системы оценки 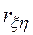 , целесообразно ввести в рассмотрение коэффициент
, целесообразно ввести в рассмотрение коэффициент
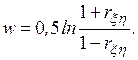
Причем 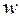 приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:
приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:
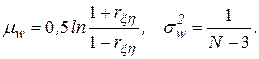
Из-за влияния числа реализаций 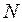 при моделировании на оценку коэффициента корреляции необходимо убедиться в том, что
при моделировании на оценку коэффициента корреляции необходимо убедиться в том, что 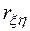 действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели М м. Это можно сделать проверкой гипотезы
действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели М м. Это можно сделать проверкой гипотезы 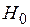 :
: 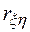 = 0. Если гипотеза при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента
= 0. Если гипотеза при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента 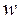 при
при 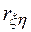 = 0 является гауссовским с нулевым средним и дисперсией
= 0 является гауссовским с нулевым средним и дисперсией 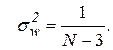 Следовательно, область принятия гипотезы
Следовательно, область принятия гипотезы 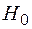 определяется неравенством
определяется неравенством
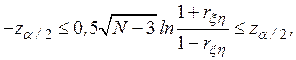
где 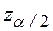 подчиняется нормированному гауссовскому распределению. Если
подчиняется нормированному гауссовскому распределению. Если 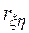 лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уровне значимости
лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уровне значимости 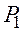 .
.
Наиболее просто близость аппроксимации определяется через коэффициент смешанной корреляции, который равен квадрату коэффициента корреляции. Для рассматриваемого нами примера, когда 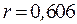 , коэффициент смешанной корреляции (или как его еще называют коэффициент детерминации) равен 0,367, что означает, что только в 36,7 % случаев отклонение
, коэффициент смешанной корреляции (или как его еще называют коэффициент детерминации) равен 0,367, что означает, что только в 36,7 % случаев отклонение 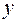 при изменениях
при изменениях 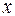 соответствует выведенному нами уравнению
соответствует выведенному нами уравнению 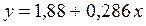 .
.
При анализе результатов моделирования системы важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные переменные стохастически зависимы, хотя причинно они являются для системы независимыми. При статистическом моделировании наличие такой зависимости может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имитации событий, положенных в основу вычисления
 2015-10-16
2015-10-16 4688
4688
