Нормальные напряжения при изгибе

Для вывода основных расчётных формул рассмотрим частный случай плоского изгиба балки – состояние чистого изгиба. Это состояние деформации наблюдается тогда, когда на каком-то участке балки действует только изгибающий момент М_х, а поперечная сила равна Q_y = 0.

Экспериментальные исследования балок при чистом изгибе показывают:

– плоские сечения балки остаются плоскими и после нагружения, испытав лишь некоторый поворот относительно друг друга;

– продольные волокна балки не давят на выше- и нижерасположенные волокна, они либо растянуты, либо сжаты;

– нейтральный слой, перпендикулярный плоскости симметрии балки, отделяет область растянутых волокон от области сжатых волокон.

На рис. 20 представлена схема деформации участка балки при чистом изгибе.

Возьмём на этом участке балки элемент, выделенный двумя сечениями I–I и II–II, находящимися на расстоянии dz друг от друга, и рассмотрим характер его деформации (рис. 20а). При принятом положительном знаке изгибающего момента М_х верхние волокна будут сжаты, а нижние – растянуты (рис. 20б).

Слой волокон, который не деформируется при нагружении, называют нейтральным. Свяжем с ним плоскость xОz.

Кривизна нейтрального слоя в результате поворота поперечных сечений I–I и II–II на угол dθ относительно друг друга равна (рис. 20в):

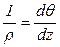. (4.3)

Отрезок cd (cd = ab = dz), удалённый от нейтрального слоя вниз на расстояние y, получит приращение длины c′d'−cd, которое можно выразить через кривизну балки:

c′d′ – cd = (ρ + y)dθ – ρdθ=yθ. (4.4)

Его относительная продольная деформация будет с учётом (4.3) равна:

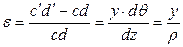. (4.5)

Тогда напряжения σ, вызвавшие эту деформацию, будут положительны и по закону Гука при растяжении определяются как

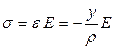. (4.6)

Здесь учтено, что для нижней зоны растяжения координата у является отрицательной (рис. 21в).

При чистом изгибе продольная сила N и изгибающий момент относительно оси у – М_у отсутствуют (N = 0; М_у = 0), но их формальное определение позволяет сделать ряд выводов (рис. 21г):

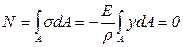, откуда 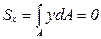; (4.7)

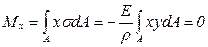, откуда 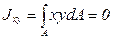. (4.8)

Равенство нулю статического момента S_x площади сечения относительно нейтральной линии (оси х) говорит о том, что нейтральная линия проходит через центр тяжести поперечного сечения.

Нулевое значение центробежного момента инерции сечения J_xy означает, что оси х и у являются главными центральными. Следовательно, рассматриваемый вид чистого плоского изгиба реализуется тогда, когда балка деформируется в главной плоскости. Значение изгибающего момента в сечении (с учётом знака момента и положения осей х, у) есть интеграл:

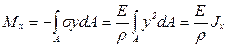, откуда 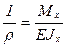. (4.9)

Величина EJ_x называется жёсткостью балки при изгибе, она характеризует способность конкретной балки сопротивляться изгибу. Подставляя (4.9) в формулу (4.6), получаем формулу для нахождения значений напряжений:

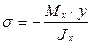. (4.10)

В формуле (4.10) знак «минус» обычно опускается (он связан с выбором направления осей координат сечения и знаков изгибающего момента). В расчётах учёт знака изгибающего момента определяет зоны растянутых и сжатых волокон, а у характеризует расстояние до соответствующих волокон. Поэтому общепринятая форма записи зависимости (4.10) следующая:

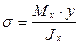. (4.11)

Таким образом, нормальные напряжения в произвольной точке поперечного сечения прямо пропорциональны величине изгибающего момента и расстоянию от нейтральной оси и обратно пропорциональны моменту инерции сечения относительно оси.

Максимальное напряжение при изгибе в сечении балки возникает в точке, наиболее удалённой от нейтральной линии:

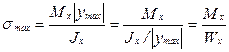. (4.12)

Величина W_x = Jx/|y_max| называется моментом сопротивления сечения при изгибе, она рассчитывается относительно нейтральной (центральной) оси Ох поперечного сечения. В наиболее же опасном сечении балки вдоль оси z

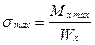, (4.13)

тогда условие прочности по нормальным напряжениям при изгибе имеет вид:

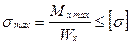. (4.14)

Условие прочности (4.14) при изгибе позволяет решать три основных типа задач:

– проектировочный расчет – подбор сечений балок (т. е. расчёт W_x) при известных нагрузках (М_х) и материале балки ([σ]) по формуле:

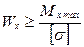; (4.15)

– проверочный расчет – проверка прочности балок по формуле (4.14);

– определение допускаемых внешних нагрузок:

[M_x] = [σ]·W_x. (4.16)

Формула (4.11) выведена для чистого изгиба.

При поперечном изгибе в поперечных сечениях возникают и нормальные, и касательные напряжения.

Возникновение касательных напряжений сопровождается появлением деформаций сдвига, в результате чего поперечные сечения балки перестают быть плоскими (гипотеза Бернулли теряет силу). Кроме того, при поперечном изгибе возникают напряжения в продольных сечениях балки, т. е. имеет место надавливание волокон друг на друга.

Более детальные исследования показывают, что, несмотря на это, формула (4.11) даёт вполне надёжные результаты и при поперечном изгибе.

4.5. Перемещения при изгибе. Дифференциальное