Напряжения при поперечном изгибе

При поперечном изгибе, помимо изгибающего момента, в поперечном сечение имеется также и поперечная сила, которая является результирующей элементарных усилий, действующих в плоскости сечения. Т.е. помимо нормальных напряжений возникают и касательные напряжения.

Касательные напряжения искривляют поперечные сечения и гипотеза плоских сечений, вообще говоря, не выполняется. Однако если длина велика по сравнению с высотой балки, то искривления по 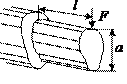перечных сечений и возникающее в случае поперечного изгиба взаимное нажатие волокон не оказывают существенного влияния на величину нормальных напряжений, и нормальные напряжения при поперечном изгибе будут определяться по тем же формулам, что и при чистом изгибе.

Дадим грубую оценку касательных напряжений при изгибе.

Пусть - длина балки, а

- характерный размер поперечного сечения.

Если сечение не является тонкостенным, то площадь его отличается от величины 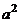числовым множителем порядка единицы. Тогда среднее касательное напряжение в сечении имеет порядок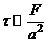

Оценим порядок нормальных напряжений.

Наибольший момент имеет порядок 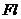, а момент сопротивления порядок 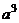(например для прямоугольного сечения 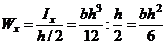). Таким образом нормальное напряжение имеет следующий порядок: 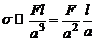, откуда видно, что если длина стержня велика по сравнению с характерным размером поперечного сечения , то касательные напряжения при расчетах на прочность обычно не принимаются во внимании. Однако, исключения составляют случаи:

1) Тонкостенные стержни

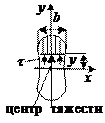2) В случае конструкций, выполненных из материалов с малым сопротивлением межслойному сдвигу, например, древесина, или, получающие в настоящее время большое распространение армированные пластики, когда касательные напряжения могут оказаться более опасными, чем нормальные.

3) Для расчета соединений (поясных швов, заклепок) в металлических балках составного сечения.

Имея это ввиду, мы приведем формулу для определения касательных напряжений при изгибе, полученную нашим соотечественником Д.И.Журавским в середине прошлого века. 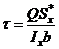, где - касательные напряжения в слое, отстоящим от нейтральной оси 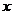на расстоянии .

- поперечная сила в сечении.

- статический момент части сечения, расположенной выше слоя в котором определяются касательные напряжения относительно оси .

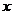- момент инерции относительно оси .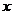

Следует иметь ввиду, что формула приближена и дает приемлемые результаты для высоких узких сечений.