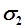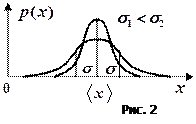
|
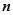 ,чем больше ошибка по абсолютной величине, тем меньше ее вероятность. Зависимость плотности распределения вероятностей измеряемой величины
,чем больше ошибка по абсолютной величине, тем меньше ее вероятность. Зависимость плотности распределения вероятностей измеряемой величины 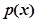 от измеренного значения
от измеренного значения 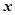 описывается кривой (рис. 2), называемой кривой нормального распределения Гаусса. Площадь, отвечающая какому-либо интервалу оси абсцисс, изображает вероятность попадания случайного результата в данный интервал. По распределению Гаусса наиболее вероятным значением измеряемой величины является ее среднее значение.
описывается кривой (рис. 2), называемой кривой нормального распределения Гаусса. Площадь, отвечающая какому-либо интервалу оси абсцисс, изображает вероятность попадания случайного результата в данный интервал. По распределению Гаусса наиболее вероятным значением измеряемой величины является ее среднее значение. Вид кривой распределения определяется величиной 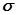 , называемой среднеквадратической ошибкой (стандартное отклонение):
, называемой среднеквадратической ошибкой (стандартное отклонение):
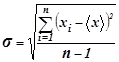 .
.
С увеличением 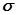 точность измерения уменьшается, и кривая нормального закона распределения имеет более пологий вид (см. рис. 2).
точность измерения уменьшается, и кривая нормального закона распределения имеет более пологий вид (см. рис. 2).
Величина 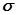 характеризует разброс отклонений от среднего значения. На практике число измерений ограничено (чаще всего не более 5-7). В этом случае пользуются распределением Стьюдента.
характеризует разброс отклонений от среднего значения. На практике число измерений ограничено (чаще всего не более 5-7). В этом случае пользуются распределением Стьюдента.
Английский математик и химик В.С. Госсет (псевдоним Стьюдент) в 1908 г. предложил методику обработки результатов многократных измерений одной и той же величины.
Существуют специальные таблицы, в которых приведены коэффициенты Стьюдента 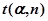 , определяемые доверительной вероятностью
, определяемые доверительной вероятностью 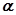 и числом измерений
и числом измерений 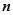 . Например, при
. Например, при 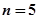 для доверительной вероятности
для доверительной вероятности 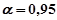 получим
получим 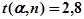 (см. таблицу в приложении 1).
(см. таблицу в приложении 1).
Согласно методике Стьюдента средняя квадратическая погрешность результата измерений среднего арифметического определяется формулой:
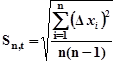 ,
,
где 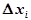 - абсолютная погрешность каждого измерения,
- абсолютная погрешность каждого измерения,
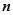 - число измерений.
- число измерений.
Границы средней квадратической погрешности:
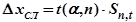 .
.
Абсолютная погрешность измерений:
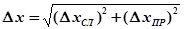 ,
,
где 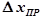 – приборная погрешность.
– приборная погрешность.
Если 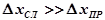 , то
, то 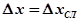 ;
;
если 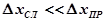 , то
, то 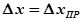 .
.
Окончательный результат записывается в виде:
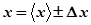 .
.
 2015-10-16
2015-10-16 20247
20247