2015-10-16
874
а) средняя ошибка средней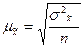 
;
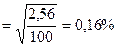б) предельная ошибка выборки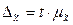 
.
По таблице значений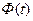 
(Приложение Б) при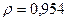 
. 
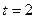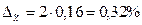
Следовательно, предельные значения средней жирности молока в генеральной совокупности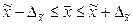 
;
;
.
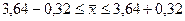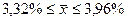Таким образом, с вероятностью 0,954 можно утверждать, что пределы изменения средней жирности молока в генеральной совокупности будут находиться от 3,32% до 3,96%.
Можно решить и обратную задачу: задав предельную ошибку выборки, определить вероятность, с которой она может быть гарантирована. При этом, зная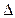 
и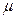 
, сначала находят коэффициент доверия
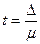, а затем по таблице Приложения Б определяют искомое значение вероятности.
Пример 2. На основе выборочного обследования 600 рабочих (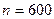
) одной из отраслей промышленности установлено, что численность женщин составляет 240 человек (
).
С какой вероятностью можно утверждать, что при определении доли женщин, занятых в этой отрасли, допущенная ошибка (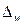
) не превышает 5% (0,05)?
