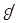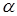Проверка статистических гипотез

Статистической гипотезой H называется любое предположение относительно закона распределения исследуемой случайной величины. Гипотезы бывают простые и сложные, простая гипотеза полностью определяет закон распределения величины x в отличии от сложной. Гипотезы бывают параметрическими и непараметрическими. В параметрических гипотезах имеется предположение о параметрах распределения и известном законе, в непараметрических гипотезах о самом виде закона распределения.

Критерием проверки статистической гипотезы называются любые правила, позволяющие принять ее или отвергнуть. Параметрические гипотезы определяются с помощью критериев значимости, а не параметрические с помощью критериев согласия. Критерии строятся с помощью статистик, для которых известно их распределение.

Ошибкой 1-го рода называется отбрасывание верной гипотезы. Вероятность ошибки 1-го рода называется уровнем значимости критерия, по которому производится проверка.

Ошибкой 2-го рода называется принятие неверной гипотезы. Если за b обозначим вероятность ошибки 2-го рода, то величина 1- b -называется мощностью критерия. Зависимость между мощностью и уровнем значимости любого критерия, выглядит так:

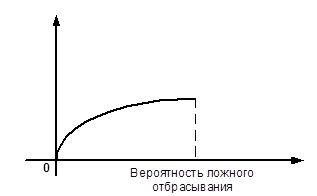Если уменьшить вероятность ошибки 1-го рода, то вероятность ошибки 2-го рода возрастет и наоборот. Чтобы вероятность ошибки 2-го рода не была значительной, нельзя a брать близким к 0, на практике a =0,05. Чем больше уровень значимости, при котором гипотеза может быть принята, тем лучше; при этом меньше вероятность ошибки 2-го рода, т.е. больше мощность критерия.

Построение критерия проверки статистической гипотезы.

Пусть выдвинута некоторая статистическая гипотеза H и задан уровень значимости a, пусть также имеется некоторая подходящая статистика, для которой известен закон распределения, в случае справедливости выдвинутой гипотезы H.

j=j(x₁,x₂,…,x_n)

Тогда по известному распределению статистики, можно найти область такую, что вероятность P(jÎw)= a - такая область называется критической. Если наблюдаемые значения статистики мы обозначим, если оно попадает в критическую область, то гипотеза отбрасывается, иначе она принимается. Такое принятие или отбрасывание гипотезы не дает логического доказательства ее или опровергается, всегда возможен любой из 4-х исходов.

1. Гипотеза верна и принимается согласно критерия.

2. Гипотеза не верна и отвергается согласно критерия.

3. Гипотеза верна, но отвергается согласно критерия- ошибка 1-го рода.

4. Гипотеза не верна, но принимается согласно критерия.

Таким образом, для проверки некоторой гипотезы необходимо указать подходящую статистику с известным гипотетическим законом распределения и построить критическую область для этой статистики по заданному уровню значимости a. Затем посмотреть, попадает ли наблюдаемое значение статистики в критическую область.