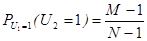Пусть генеральная совокупность содержит N членов, из которых M обладает некоторым признаком A, тогда 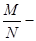 генеральная доля.
генеральная доля.
Для оценки этой неизвестной генеральной доли образуется повторная выборка n, возвращая каждый отобранный член обратно, восстанавливают первоначальный состав генеральной совокупности, поэтому результат отбора любого члена в выборку не влияет на результаты последующих отборов, т.е. выполняется условие схемы независимых испытаний, в каждом из этих испытаний могут появиться или не появиться члены, обладающие признаком A с вероятностями
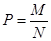
и q= 1 -p не появится.
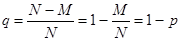
Следовательно, случайные величины z1,z2,…,zn , выражающие число членов с признаком A при отборе 1-го, 2-го, n -го члена выборочной совокупности являются независимыми и одинаково распределенными, причем каждый из них с указанными вероятностями может принимать лишь 2 значения - 1 или 0.
Таким образом, закон распределения выборочной доли z, повторной выборки n -это есть
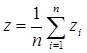 ;
;
Она является суммой из n независимых одинаково распределенных случайных величин, имеющих абсолютные центральные моменты 3-го порядка, поскольку каждый принимает лишь 2 значения. На основании следствия теоремы Ляпунова выборочная доля повторной выборки достаточно большого объема n распределена по нормальному закону, математическое ожидание 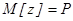 , а дисперсия
, а дисперсия 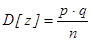 .
.
Рассмотрим бесповторную выборку объема n, образованную из этой же генеральной совокупности. Обозначим через U1,U2,…,Un случайные величины, которые выражают число членов с признаком A. При этом отборе первого, второго, n -членов выборочной совокупности, каждая их них может принимать лишь 2 значения - 1и 0.
Если i -член обладает признаком,то 1, не обладает -0,.
Условие при отборе 1-го члена повторной и бесповторной выборки одинаковы, следовательно, закон распределения случайной величины U1 такой же как у случайных величин zi. Покажем, что такой же закон распределения имеет и случайная величина U2, для нахождения вероятности того, что U2= 1 используют формулу полной вероятности, роль события Ai играют два события U1= 1, U1= 0, а искомое событие U2= 1.
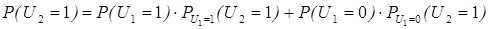
Вероятность: 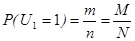
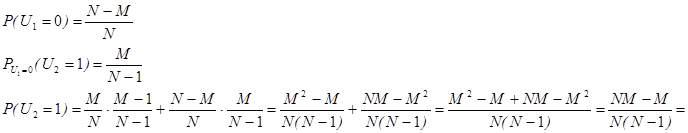
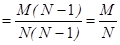
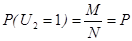 .
.
Вероятность того, что случайная величина примет значение 0, т.е. 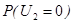 будет находиться по правилу:
будет находиться по правилу: 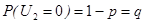 .
.
Закон распределения случайных величин U1 и U2 совпадают. Аналогично рассмотрев большое число возможностей, можно показать, что тот же закон распределения и случайной величины U3,U4,…,Un. Эти величины одинаково распределены и их математические ожидания равны генеральной доле p, а дисперсии равны p×q.
Отличие бесповторной выборки от повторной состоит в том, что случайные величины Ui, 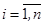 зависимые, каждая зависит от предшествующих ей случайных величин. Выборочная доля бесповторной выборки- это среднее арифметическое
зависимые, каждая зависит от предшествующих ей случайных величин. Выборочная доля бесповторной выборки- это среднее арифметическое 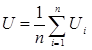 .
.
Выборочная доля U бесповторной выборки распределена по нормальному закону, хотя величины Ui -зависимые. Найдем параметры этого закона математического ожидания и дисперсии случайной величины U. Математические ожидания случайной величины Ui одинаковы, они равны генеральной доли P. Математическое ожидание выборочной доли в соответствии с теоремами математического ожидания также будут равны генеральной доли P, M[U]=P.
Найдем дисперсию выборочной доли D[U],т.к. U есть сумма, то дисперсию находим от суммы
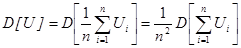
применим правило нахождения дисперсии:
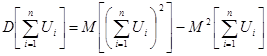
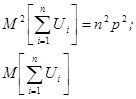
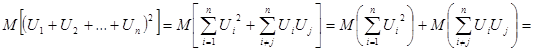
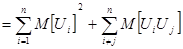 . (1)
. (1)
Поскольку случайные величины Ui распределены одинаково, также распределены одинаково и их квадраты, поэтому достаточно математическое ожидание квадрата одной из них Ui, учитывая определение квадрата случайной величины.
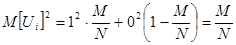 ;
;
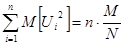 ;
;
Случайная величина 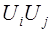 также может принимать значения лишь 1 и 0, значение 1 она принимает, если
также может принимать значения лишь 1 и 0, значение 1 она принимает, если 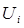 и
и 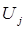 примут значения 1, а 0 в остальных случаях, тогда по теореме умножения вероятностей для зависимых событий
примут значения 1, а 0 в остальных случаях, тогда по теореме умножения вероятностей для зависимых событий
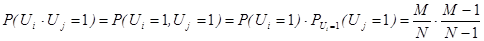 ;
;
Т.к. вероятность того, что случайная величина Uj примет значение 1 при условии, что величина Ui приняла значение 1, равна отношению 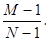
Вероятность того, что случайная величина 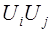 примет значение 0 согласно правилу нахождения вероятности противоположного события будет равна
примет значение 0 согласно правилу нахождения вероятности противоположного события будет равна
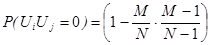
Таким образом, математическое ожидание случайной величины 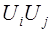 составит
составит
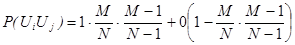
Второе слагаемое в равенстве 1 представляет собой сумму одинаковых слагаемых
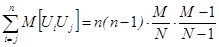 ;
;
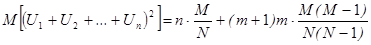 ;
;
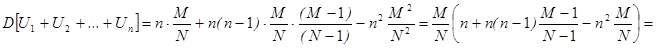
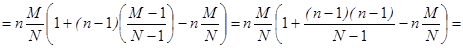
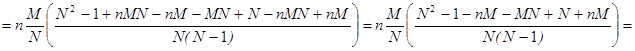
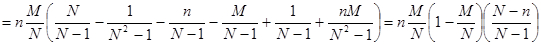 ;
;
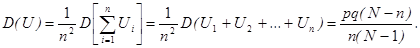
Т.к., 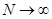 , то различие n(N-1) практически неощутимо, поэтому 1 опустим и разделим почленно на n.
, то различие n(N-1) практически неощутимо, поэтому 1 опустим и разделим почленно на n.
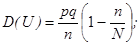
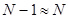 (2)
(2)
при повторном и бесповторном отборе элементов в выборку, выборочная доля является несмещенной и состоятельной оценкой генеральной доли.
Из формулы 2 видно, что при увеличении числа наблюдений дисперсия выборочной доли становится как угодно малой, а вероятность события 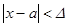 , как угодно близко к 1,т.к. эта вероятность равна значению функции Лапласа
, как угодно близко к 1,т.к. эта вероятность равна значению функции Лапласа 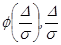 -становится большой при значении >5.
-становится большой при значении >5.
 2015-10-16
2015-10-16 899
899